一种超窄码元宽度PSK 信号识别方法
2018-10-23胡瑾贤
姚 群,胡瑾贤,柴 恒
(中国船舶重工集团公司第七二三研究所,江苏 扬州225101)
0 引 言
雷达信号的脉内特征是电子侦察中对雷达信号分选和识别的重要参数。随着雷达技术的快速发展,常规脉冲雷达信号在雷达信号环境中的比例已减小,相移键控(PSK)信号的距离分辨力高,抗干扰能力优良,低截获概率,同时还可以为雷达提供大的信噪比处理增益,广泛应用于雷达波形产生中[1]。
在雷达调制识别技术中,时频分析方法因其直观、方便、识别效率高等特点被广泛应用。文献[2]利用瞬时自相关获取时频特性,基于瞬时频率提取特征参数,实现对4种不同调制类型信号的识别。文献[3]基于相对无模糊相位重构算法,构建了基于相位差分峰值幅度比较的二进制相移键控(BPSK)及四相移相键控(QPSK)调制信号调制方式识别方法。文献[4]提出了一种综合对称相关函数与瞬时频率法的新处理方法。文献[5]提出一种基于相位差分算法的脉内识别方法。以上基于时频特性的分析方法都没有涉及超窄码元宽度的情况。
本文在基于瞬时频率的脉内调制特征识别方法基础上[6-8],提出了一种超窄码元宽度PSK信号的识别方法,该方法可以在低信噪比情况下识别出超窄码元宽度PSK信号。
1 时频曲线的提取
通过解析信号的相位信息可以直接求取信号的瞬时频率,该方法简单,运算量小[9-10]。解析信号可以通过对接收到的实信号进行希尔伯特变换获得,对变换后的复信号r(n)可以建模为:
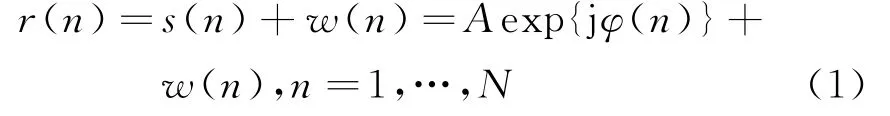
式中:A为载波幅度;φ(n)为相位;w(n)为方差等于σ2的附加性高斯白噪声;N为样本个数,对于正弦波信号和相位编码信号(以二相码为例),分别可以表示为:

式中:fc和φ0分别为载频、初相;T为采样间隔;N为二相码个数;Tb为码元宽度;∏ 为持续时间为Tb的窗函数。
由复信号通过反正切可以得到瞬时相位:
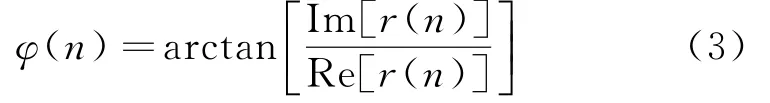
此时只能得到带模糊的相位,为了得到真实的相位需要对相位进行解模糊[11]。一般情况下可以由相邻样本点之间的测量相位差解模糊得到信号的真实相位,第n个样本点的真实相位值为:

式中:φT(n)为解模糊后的真实相位,定义
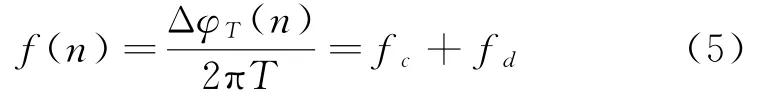
理想情况下信号的瞬时频率在码元跳变点处存在跳变,跳变幅度由相位跳变大小决定,以二相码为例,相位跳变为π,频率跳变为fs/2,其它点频率跳变为0。
但是在信噪比较低时,受噪声影响,相邻样本的相位顺序关系可能取反,导致解模糊后的相位被噪声污染。此时采用单个相位差获取瞬时频率的方法误差很大,因此为了提高低信噪比下时频曲线的正确性,本文采用了改进的Kay算法。
Kay算法由Steven Kay提出,基于相位平均法运算,方法简单,当信噪比较高时估计精度达到克拉美罗限,在许多领域获得了广泛应用。Kay给出的频率估计公式如下:


该算法在信噪比较高的情况下性能良好。当信噪比低于8 dB时,受噪声影响,直接取反正切获得幅角时可能出现2π的相位模糊。一旦出现相位模糊,频率估计值fc将会有较大误差,相位平均法的性能迅速恶化。如果对接收信号进行相位展开,利用展开之后的相位估计相邻样本的相位差,然后再进行频率估计,既保留了相位平均提高时频曲线正确性的优点,同时解决了相位模糊带来的误差,可以显著改善Kay算法的性能,改进的Kay算法的频率估计公式为:
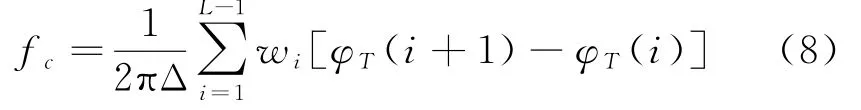
改进的Kay算法受相位展开的正确性影响,在信噪比低于8 dB的情况下直接进行相位展开,效果并不理想。但是在实际的电子侦察中,接收机的带宽一般情况下是远大于信号带宽的,因此对原始信号先进行频域滤波,滤除信号带外的噪声,提高信号带内的信噪比,再进行相位展开,可以提高相位展开的正确性。
2 超窄码元宽度PSK信号的识别
常见调制类型信号的瞬时频率曲线,如图1所示。在信噪比较高的情况下,直接利用提取出的瞬时频率曲线的特征即可区分出不同类型的调制信号,识别方法如下:(1)计算时频曲线的跳变点,无调制和线性调频信号不存在跳变点,可以分离出PSK和频移键控(FSK)信号。(2)计算瞬时频率曲线的直方图,FSK的直方图分布相对均匀,PSK信号的直方图存在峰值,可以根据此特征识别出PSK信号。

图1 不同调制类型的瞬时频率
但是在低信噪比的情况下,对滤波后信号利用改进Kay算法获得的时频曲线存在2个问题:一是影响跳变点幅度,二是影响跳变点宽度。改进Kay的窗宽L越大,平滑的效果越明显;跳变点的幅度越小,跳变点宽度越宽。为了正确识别低信噪比的信号,降低噪声影响,可以取大的L值。一般在信噪比较低的情况下取L=64可以得到相对平滑的曲线并保留信号的时频特性,能够正确地分析出脉内调制类型。但是在实际环境中存在超窄码元宽度(码元宽度小于50 ns)的PSK信号,假设PSK的码元宽度为50 ns,窗宽L=64,此时窗宽大于码元宽度,导致2个突变的峰值平滑成1个虚假的具有频率编码(FSK)特性的时频曲线。在这种情况下,利用时频曲线进行信号调制类型识别会产生错误,只有自适应地选择L的长度才能够解决超窄码元宽度PSK信号识别问题。本文在第二部分的基础上,提出最终的改进算法如下:
(1)对中频信号进行滤波,对滤波后的信号进行希尔伯特变换,获取解析信号。
(2)利用解析信号获得瞬时相位,并对瞬时相位进行展开得到无模糊的相位。利用改进Kay算法获取时频曲线,取窗宽L=64。
(3)利用时频曲线进行分析,如果脉宽与跳变点个数的比值超过阈值,则自适应地修正窗宽L,重新获取时频曲线。
(4)利用最终的时频曲线的跳变点的类型识别出PSK信号。
识别完成后,利用时频曲线进一步分析PSK信号的编码规律,首先找出频率跳变点的位置,求出频率跳变间隔,计算出最小的频率跳变间隔,得到子码宽度。
3 仿真结果
本节利用Matlab进行仿真,对本文的结论进行验证。首先分析不同窗宽L对时频曲线性能的影响。仿真信号为BPSK信号,采样频率Fs=1 000 MHz,信号载频Fc=100 MHz,码元宽度0.8μs。由图2可以看出,增大窗宽会影响频率跳变点的幅度和宽度,但是保留了信号的调制特性并对噪声的抑制明显,可以有效提高调制类型识别的正确率。
在低信噪比下需要对原始信号滤波,进一步提高时频曲线的质量。图3的仿真信号同上,取L=64,可以看出,低信噪比情况下,即使增大了L,时频曲线也会产生错误的跳变,但是滤波后的瞬时频率可以正确地分辨出码元的跳变点和码元宽度。
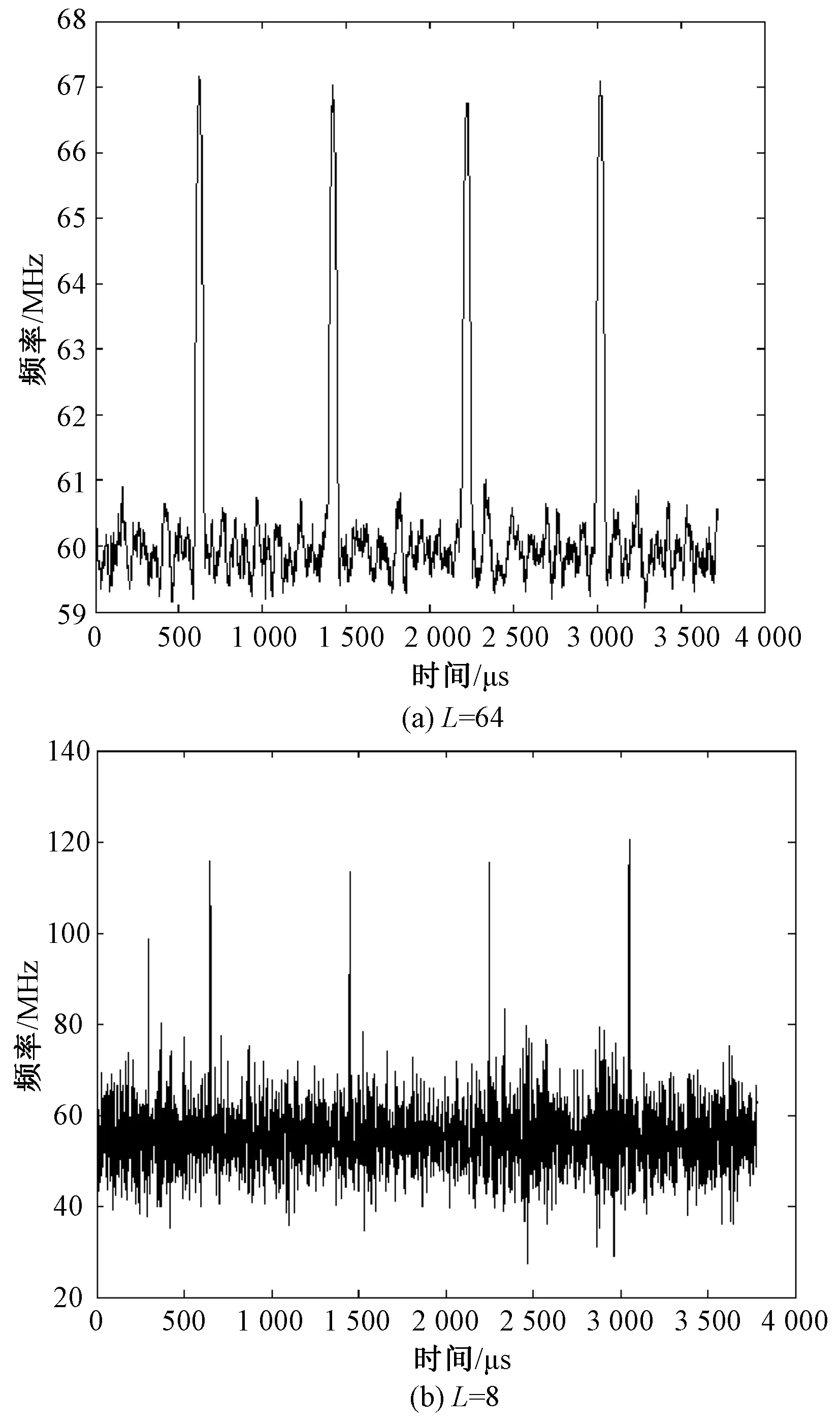
图2 不同窗宽L下的瞬时频率(SNR=10 dB)
通过滤波以及增大窗宽L可以获取高质量的时频曲线,但是在码元宽度超窄的情况下使用固定大窗宽也会产生错误。图4对比了在信噪比为6 d B的情况下,在不同窗宽L下改进Kay算法得到的时频曲线图。其中仿真信号为BPSK信号,采样频率Fs=1 000 MHz,信号载频Fc=100 MHz,码元宽度50 ns。由图4可以看出,L=64的情况下,由于平滑过大,信号的时频曲线与FSK信号相似。L=8时,信号时频曲线可以正确地显现出PSK的特性,而由于此时平滑较小,受噪声影响大,跳变点的幅度并不规整,需要进一步利用相位信息判别信号是哪种类型的PSK信号。
表1给出了在SNR=3 dB和SNR=6 dB的情况下,对码元宽度50 ns的BPSK信号进行200次重复实验得到的结果。在固定窗宽下,错误识别为FSK的概率很高,而使用动态窗宽后可以正确识别50 ns码元宽度的PSK信号,SNR=3 dB时识别正确率可达99%。
4 结束语
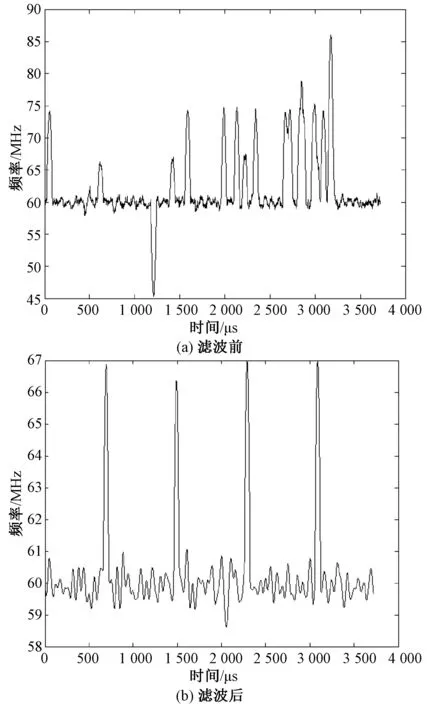
图3 瞬时频率(SNR=3 dB)

表1 码元宽度50 ns下的识别结果对比
本文基于瞬时频率的脉内调制特征识别技术,利用解模糊后的相位与改进Kay算法在较低信噪比下获取质量较好的时频曲线。采用动态改变改进Kay算法窗宽的方法可以在不降低其他调制类型正确率以及速度的情况下,正确识别超窄码元的PSK信号。MATLAB仿真结果表明,本算法可以在较低信噪比条件下对超窄码元的PSK信号进行有效识别。本算法不需要接收信号的先验知识,适合于雷达电子对抗中应用。

图4 瞬时频率曲线(SNR=6 dB)
