Nuttall窗三谱线插值法在雷达辐射源识别中的应用
2018-10-23石远东
李 霄,石远东,柴 恒
(中国船舶重工集团公司第七二三研究所,江苏 扬州225101)
0 引 言
随着雷达技术的不断突破,雷达信号复杂、工作模式多变等特性给电磁辐射源识别带来了诸多困难。基于载频(RF)、波达角(DOA)、脉间特征(PRI)、脉内特征(PMF)等变化规律的辐射源识别难以满足指标要求,因此雷达的无意调制特征逐渐被重视。
雷达辐射源的谐波特征属于无意调制特征。谐波特征的特点是在其他有意调制特征和雷达工作模式不断变化的条件下,始终保持一定的规律性和稳定性[1],因此可用于辐射源识别。快速傅里叶变换(FFT)谐波分析的有力工具,在应用FFT进行谐波分析时,需要对采样信号进行截断处理。这个过程无法满足截断后的信号是自身的整数倍周期,因此经过FFT分析后的信号不可避免地产生频谱泄漏,导致幅度较小的谐波分量被基波的泄漏影响,造成谐波幅度削弱甚至被淹没,不能达到谐波测量的技术要求[2]。因此,FFT运算之前需要对原始采样信号加窗处理。由于不同的窗函数在性能上各有侧重,需要根据实际需求对窗函数进行选取。此外,FFT存在栅栏效应,需要对分析结果进行插值修正,以精确恢复谐波幅度特征。
1 雷达辐射源谐波特征
雷达在发射端采用高功率的信号增益放大器增加探测距离,以常见的正弦信号为例,如式1所示:

式中:s(t)为进入功放前的正弦信号;r(t)为幅度;f0为载波频率;θ为初始相位。
不考虑增益器件的AM-PM转移特性,则信号经过放大后可表示为:
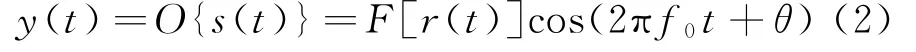
对y(t)进行泰勒公式展开为:
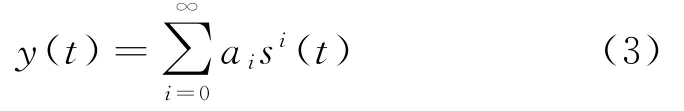
式中:ai为各个谐波分量的幅度增益,与放大器的特性直接相关。
以三阶模型为例,令r(t)=A,2πf0=ω,对功率放大器激励后的y(t)进行三阶泰勒展开为:
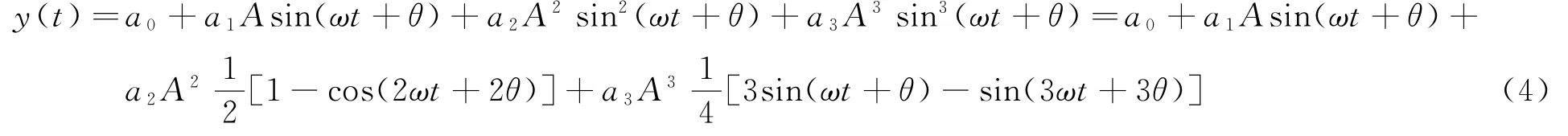
信号y(t)通过辐射源天线发射、经过空间线性信道传输,最后被接收机端接收。忽略直流分量,用幅度增益和相位偏移来近似这个过程:
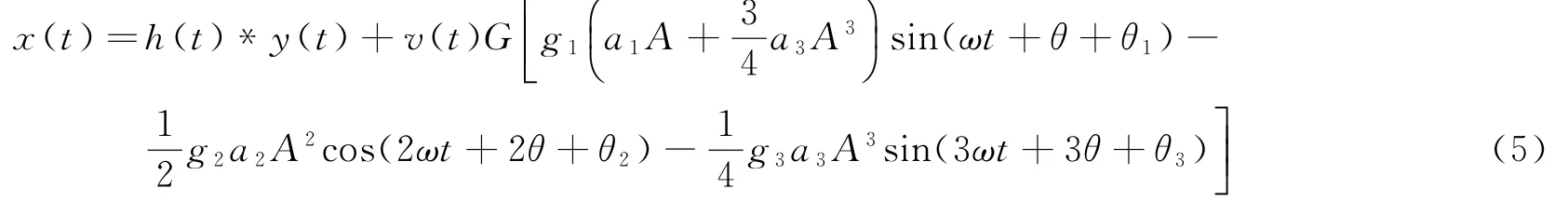
式中:v(t)为接收系统混入的高斯白噪声;G为从发射到接收的增益,它随传输距离的增加而衰减;gi为接收系统对各个谐波的增益。
由式(5)可得各个谐波的幅度为:
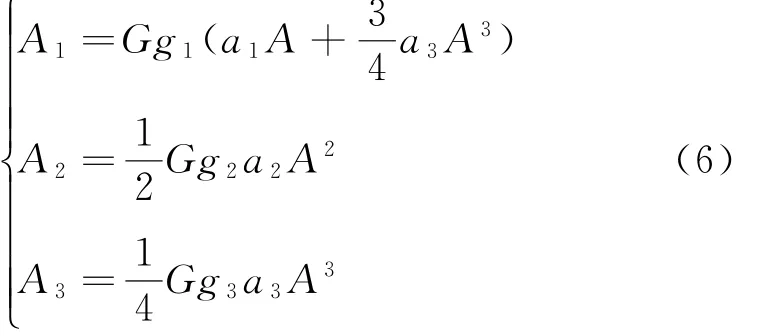
根据放大器放大特性,并结合实际情况可知,各次谐波的能量远小于基波能量,所以有:
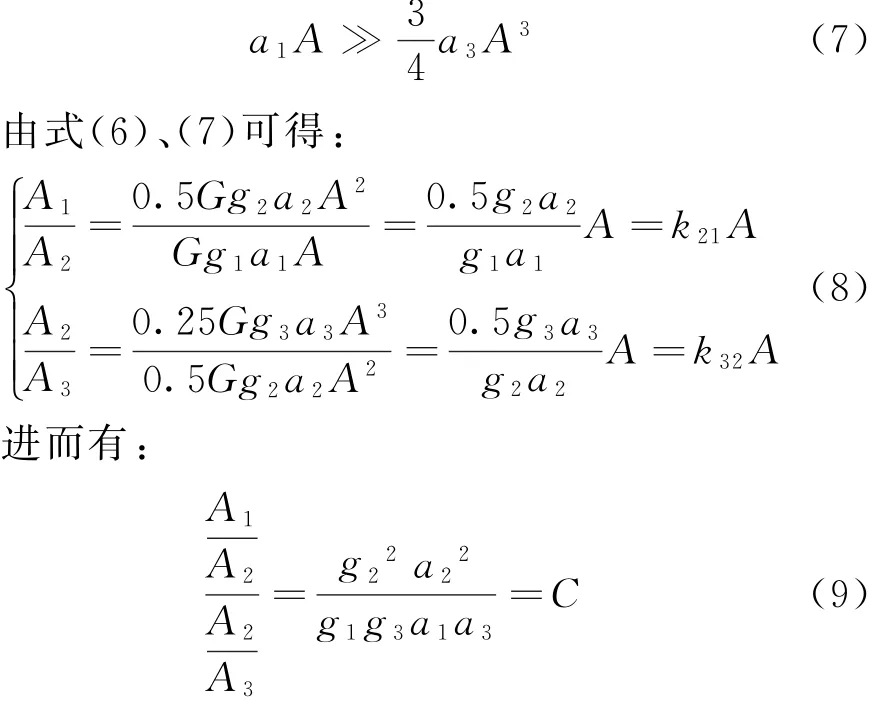
其他多次谐波的幅度关系可依次类推。由式(9)可知,在雷达发射系统和侦察接收机系统参数不改变的情况下,即ai和gi不变的情况下,不同雷达辐射源发射的相同信号被接收系统侦收时,各次谐波的幅值有特定的比例关系。如果能够精确分析出1部辐射源各个谐波的幅值,就能对雷达辐射源的特征进行提取,对不同的雷达辐射源进行识别。
2 窗函数的选择
利用FFT进行频谱分析是电子对抗系统采用的最广泛、最成熟的方法。FFT过程中不可避免频谱泄漏问题,泄漏是截取过程中的突变所致。频谱泄漏能量虽然有限,但足以对谐波分量的有效提取造成很大影响,甚至淹没谐波分量。因此需要在FFT运算前对接收的信号进行加窗,降低频谱泄漏的影响。不同的窗函数具有不同的特点,常见的窗函数有矩形窗、Hanning窗、Hamming窗、Blackman窗、Nuttall窗[3]等。
四项五阶Nuttall窗的窗函数为:
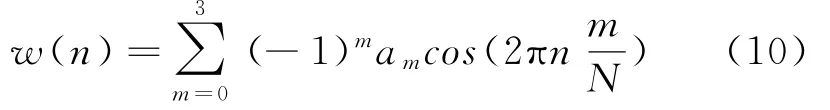
式中:a0=0.312 5;a1=0.468 75;a2=0.187 5;a3=0.0312 5;n=0,1,…,N-1,N为FFT运算点数。
它的特点是表达式由多个余弦分量组成,形式简单,易于计算。将矩形窗、Hanning窗、Hamming窗、Blackman窗、四项五阶Nuttall窗的归一化频谱绘制到图1中。

图1 常见窗函数的频谱
窗的选择是一个权衡利弊的过程,窗函数的性能主要考虑因素为主瓣宽度、第一旁瓣电平、旁瓣随频率而减小的速度。由于窗函数泄露降低带来的增益通常超过主瓣增益损失,且各次谐波在频域上与基波相距较远,所以主瓣宽度影响不是主要因素,主要考虑第一旁瓣的电平和旁瓣衰减率。依照上述标准,矩形窗作为其他窗性能的对比标准,主瓣最窄,但是第一旁瓣电平最高,旁瓣衰减慢。其他窗函数性能要求从低到高排序依次为Hanning窗、Hamming窗、Blackman窗、四项五阶Nuttall窗。
由图1可知,与其他几种窗函数相比,四项五阶Nuttall窗第一旁瓣衰减最大,超过了-60 dB,而且其他各级旁瓣衰减速率最高,因此非常适合谐波的提取。
3 谐波幅度的修正
傅里叶变换还原的谐波幅度与真实谐波幅度的偏差不仅有频谱泄漏带来的影响,还有离散傅里叶变换(DFT)过程中,DFT的径与实际频率点存在的频率偏差导致的栅栏效应,栅栏效应导致谐波的幅度以径为中心呈现扇形损失。使用插值拟合方法减少DFT的扇形损失,可以对辐射源的谐波幅度做进一步真实逼近,对辐射源谐波个体特征的提取有重要的意义。
输入信号y(t)的采样形式y(n)为:

式中:Ai为各次谐波的采样幅值;fi和θn为对应的谐波频率和相位;H为谐波的次数;n为信号的采样点数。
对y(n)加窗函数w(n),得到Yw(n)为:

谐波频率点fi不与kiΔf重合,存在最高为0.5kiΔf的频率差值。设谐波频率点fi对应的抽样最大值的横坐标为ki2,以ki2为中心,左右各一个频率值为ki1,ki3,则有:

式中:ki∈[0,1,…,N-1],则ki1,ki2,ki3对应的谐波幅度值依次为;令偏差值α=ki-ki2,则α∈[-0.5,0.5];令则把式(14)代入β并化简可得:
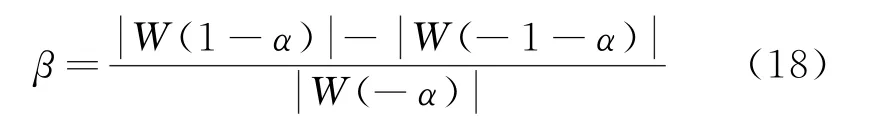
式(18)建立了从β到α的映射关系,利用映射关系的反函数,可由β多次拟合求得偏差值α,此时:

得到第i次谐波的频率修正值fi,然后运用ki1,ki2,ki3三谱线差值,由于ki2最近似于真实值,所以分配比例系数为2,此时根据式(14),有:
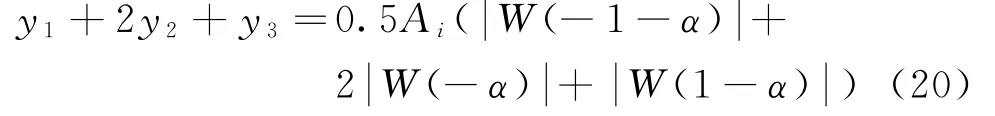
化简得:
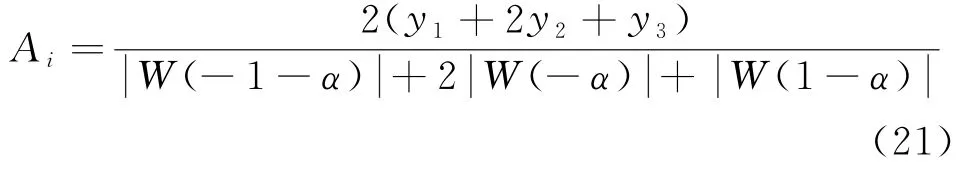
在N较大的情况下,式(21)可化简为:
为了让学生更快更容易地理解并学懂高中化学基本原理,要在化学实验课堂中引入多样化的信息化技术,这样既能够保证学生在进行化学实验学习时的新鲜感,又能够缩短化学实验的教学时间,提升教学效果.而信息化技术包含的方面比较广泛,在其中对于高中化学实验教学起到促进作用的有下述的具体几种.

再由式(14)、(15),可得到对应的谐波分量Ai的相位分量θi为:
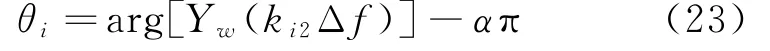
在α∈[-0.5,0.5]值域范围内指定某一值,由
式(18)、式(21)多次拟合,确定拟合多项式的系数,推导出谐波幅度修正多项式为:

把式(24)在式(19)、式(22)、式(23)中迭代,就可以依次得到辐射源多次谐波的修正频率、幅度及相位。
三谱线插值法可以很好地配合四项五阶Nuttall窗进行谐波分析,应用于辐射源5次谐波模型,进行仿真实验,可以验证算法的有效性。
4 仿真及实验分析
令输入信号为:
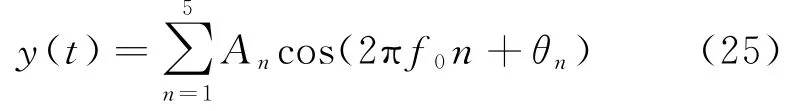
符合式(3)的形式,令An=[200,9.7,20.5,10.2,4.8],θn=[0.05°,39°,60.5°,123°,-52.7°]。根据图1的情况,对上述窗函数中3种性能较好的函数加窗并进行1 024点FFT后,结果及谐波放大结果如图2所示。
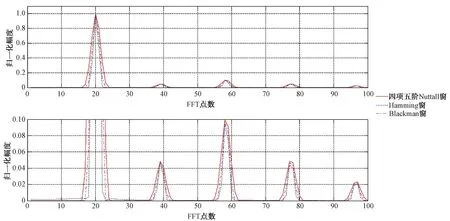
图2 窗函数的谐波分析
由表1可知,四项五阶Nuttall窗能够很好地对谐波幅度近似。
使用与窗函数分析同样的五次谐波模型,各次谐波幅值为An=[200,9.7,20.5,10.2,4.8],初始相位为θn=[0.05°,39°,60.5°,123°,-52.7°],转化为[-π,+π]范围内的表达形式,为θn=[0.000 87,0.680 7,1.055 9,2.146 8,-0.919 8],对式(25)的信号进行分析,结果如图3所示。
令幅度的误差计算公式为:
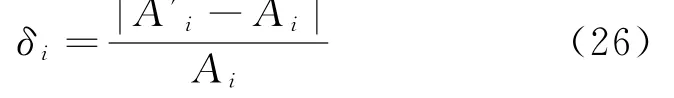
由表2和表3可以看出,利用四项五阶Nuttall窗函数配合三谱线插值法对y(t)的谐波幅度进行估计能够将误差控制在10e-7量级,具有很高的准确度。

表1 不同窗函数的谐波幅度
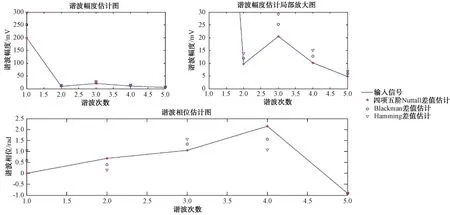
图3 谐波幅度与相位估计

表2 各次谐波幅度估计值

表3 各次谐波幅度误差
5 结束语
本文研究了雷达信号辐射源对雷达信号各次谐波之间的非线性放大关系,分析了谐波特征提取过程中窗函数的使用方案。提出了利用四项五阶Nuttall窗结合三谱线差值,对信号的各次谐波幅度进行精确还原,然后利用各次谐波幅度之间的比值对不同辐射源进行识别的方法。仿真结果表明,四项五阶Nuttall窗相比于其他常用窗函数,具有良好的谐波提取特性,结合三谱线插值法,能够对雷达辐射源谐波信号幅度进行精确还原,对于雷达辐射源识别分析有一定的实用价值。
