猴子岩地下厂房围岩变形监测成果分析
2018-10-22胡升伟
胡 升 伟
(中国电建集团成都勘测设计研究院有限公司,四川 成都 610072)
1 概 况
猴子岩水电站采用首部式地下厂房,布置在大渡河右岸坝轴线上游一侧的山体中,厂房纵轴线方位为N61°W。依次设有主厂房、主变室、尾水调压室,三大洞室呈“一字型”平行布置,中间为主变室,两边分别为主厂房和尾水调压室,每两台机组由一条尾水连接洞连接主厂房、主变室及尾调室。两相邻洞室间隔的岩柱厚度相同,取为45m(吊车梁以上)[1]。
地下厂房、主变室、尾调室附近的岩体完整性总体较完整,一般微风化,无卸荷。右岸高地应力区位于水平埋深250 m以后的地层,洞址区最大主应力方向接近区域构造应力最大主应力方向,这是区域构造应力场与地形自重应力场叠加的结果,洞址区地应力随地层的水平埋深增大而增加,局部应力集中,属于高地应力量级区域。地下厂房无区域断裂通过,仅主机间上游一条宽1.0 m~1.5 m的断层F1-1发育,以及次级小断层、挤压破碎带和节理裂隙等结构面,厂房部位岩体完整性总体为较完整~完整,围岩以Ⅲ1类为主[2]。
本文根据猴子岩水电站地下厂房现场监测数据,考虑围岩开挖高程进度及温度变化和时效对围岩变形的影响,采用回归分析方法探究各分量对围岩变形的影响程度,借助位移等值线图全面地了解围岩变形的发展情况。
2 变形统计模型
通过大量地下洞室围岩变形规律的研究以及岩石力学围岩变形理论,岩石的蠕变曲线分为四部分:瞬时弹性应变、应变不断增加而应变速率不断减慢的过渡蠕变、以恒定速度增长的常蠕变、加速增长直至破坏的加速蠕变,实际工程通常用流变模型来模拟岩石蠕变的过程。
根据粘弹性地层变形的本构关系和工程实际经验,在地下厂房围岩变形中开挖高程、温度、时效、地质构造条件、开挖方式、外部荷载及支护方式等对其会造成一定的影响,其中尤以开挖高程、温度和时效的影响最为显著。开挖高程的变化会引起应力重分布,对初始地应力场造成一定影响,从而引起岩体的变位。温度变化会对岩体产生收缩或膨胀,其受限制后产生的温度应力对岩体变位造成影响。岩体蠕变变位主要受时效的影响,而开挖导致的卸荷裂隙开展,围岩应力重分布,徐变、压缩回弹等现象随时间推移对围岩变形增长造成的影响不可逆转,可统一归结为时效位移[3]。
2.1 开挖高程进度分量
开挖进度实际上反映了监测点至开挖部位的距离,距离越近,开挖的影响越大。岩体最初受初始应力场的影响,该应力与上覆岩层的重力有关,开挖会造成上覆岩层的缺失,即临空面的应力为零,在孔壁处三向应力状态变为双向应力状态。将这种开挖效应的模拟考虑为施加在围岩开挖边界上的释放荷载[4]。开挖高程进度分量主要是由开挖造成应力释放而引起的围岩边墙变形,一般认为地下厂房洞室内任一点的位移可能与开挖面与仪器测点的高程差及其二、三次方或四次方成比例。因此,围岩变形的开挖高程进度分量δH可由下式表达:
δH=a0+a1(H1-H0)+a2(H1-H0)2+a3(H1-H0)3+a4(H1-H0)4
(1)
式中:H0监测仪器安装高程,m;H1围岩开挖高程,单位:m。
2.2 温度分量
引起围岩位移的温度因素,主要是温度变化引起的温度应力及岩体热胀冷缩变形受到周围岩体的约束作用而发生向孔口处位移。由弹性力学分析可知,围岩在变温场作用下任一点的变位与各点的温度变化值呈线性关系。在计算过程中,洞室边界岩体温度的变化,是由于气温的季节性变化引起,故可采用一天之中温度实测值的均值表示温度位移分量。围岩变形的温度分量δT可由下式表达:
δT=(b0+b1T)
(2)
式中:T观测日当天平均气温,℃。
2.3 时效分量
地下厂房围岩的徐变、支护接触面或裂缝的变化及岩体节理裂隙的压缩等因素,都会导致围岩的非弹性变形,这种变形随时间增长而变化,过程不可逆,也称时效位移。正常运行状态下的地下厂房围岩时效位移在初期变化较快,后期变化较慢,最终趋向稳定[5]。根据时效位移的变化规律并结合工程实践经验(考察实测位移过程线),围岩变形的时效分量δt可由下式表达:
δt=c0+c1t+c2ln(t)+c3t/(t+100)
(3)
式中:t计算年份1月1日算起至观测日的累计天数,d。
2.4 围岩变形统计模型
地下厂房围岩变形采用多点位移计监测,一般假定监测仪器最深点为不动点,其余各点相对不动点沿孔口方向的位移即为围岩的变形量。以围岩的变形量为效应量δ,以开挖高程进度分量δH、温度分量δT和时效分量δt为自变量,其余可考虑为常量,则地下厂房围岩变形统计模型可由下式表达:
δ=δH+δT+δt
(4)
式中:δH开挖高程进度引起的弹性位移分量;δT温度变化引起的弹性位移分量;δt非弹性位移分量,即时效位移分量。
围岩变形统计模型最终表达为:

(5)
式中:C常数;H0监测仪器安装高程,m;H1围岩开挖高程,单位:m;T观测日当天平均气温,℃;t计算年份1月1日算起至观测日的累计天数,d。
3 回归分析
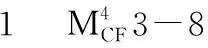
表实测位移量、温度和开挖面高程与对应时间表
y=-956.818+2.245(H0-H1)+1.216T0-182.385ln(t)+2504.051t/(t+100)
(6)

逐步回归后复相关系数R=0.994,回归效果很好,且残差基本在0值附近波动,表明所选统计模型符合围岩变形实际情况。

图实测位移与回归值比较过程线图
采用回归方程式(6)来考察各分量对效应量的影响大小,式(6)中开挖高程进度分量、温度分量和时效分量分别为:2.245(H0-H1)、1.216T0和-182.385ln(t)+2504.051t/(t+100),将每次观测取得的开挖面与测点高程差代入开挖高程进度分量,温度实测值代入温度分量,开挖天数代入时效分量,选择各分量最大值和最小值的差值作为效应量的影响值。
各分量最大值和最小值的差值ΔH、ΔT、Δt对效应量影响权重采用下式计算:
ρi=(Δi)/(ΔH+ΔT+Δt)
(7)
式中:i代表开挖高程进度分量、温度分量和时效分量;ΔH计算的开挖高程进度分量最大值和最小值的差值;ΔT计算的温度分量最大值和最小值的差值;Δt计算的时效分量最大值和最小值的差值。

4 位移等值线
根据地下厂房现场实测监测数据,选取2#机组3-3监测剖面多点位移计2016年3月19日监测数据绘制上、下游边墙和顶拱的围岩变形等值线详见图2。
由图2可知,地下厂房深层围岩变形量基本在10 mm以下,浅层围岩变形量大多在30 mm以上,尤其是两侧边墙中上部。地下厂房开挖后,靠近监测仪器孔口位置的围岩受到的周围岩体约束作用减小,出现应力释放而产生向仪器孔口方向的变形;而深层围岩受到的约束作用较大,不易发生变形,且越向岩体深处,约束越大,变形越小。因此,在进行地下厂房围岩变形监测时,应重点关注监测仪器的孔口变形。另外,围岩变形在时间和空间上与围岩应力变化存在很好的关联性,也需关注其附近部位的支护荷载变化情况,如锚杆应力计和锚索测力计的监测成果,这样有助于更加全面地了解围岩变形规律。
5 结 语
(1)通过描述围岩变形与开挖高程进度、温度和时效的关系,采用逐步回归的方法,计算所得复相关系数R=0.994,回归效果很好,且残差基本在0值附近波动,表明所选统计模型符合围岩变形的实际情况。各回归分量对围岩变形的影响程度为:影响最大的是开挖高程进度分量,其次是时效分量,影响最弱的是温度分量。

图2 2#机组3-3监测剖面位移等值线图
(2)位移等值线表明监测仪器孔口位置围岩变形较大,监测时应重点关注其变形情况,围岩变形在时间和空间上与围岩应力变化存在很好的关联性,也需关注其附近部位的支护荷载变化情况,有助于更加全面地了解围岩变形规律。
