基于自适应相机运动速度的视频稳像算法*

胡 琪，罗健欣，胡谷雨，李 杰

(1.中国人民解放军陆军工程大学 指挥控制工程学院,江苏 南京 210001；2.中国人民解放军陆军工程大学 职业教育中心,江苏 南京 210001)

0 引言

数字视频稳像是一种通过去除不必要的相机抖动来提高视频质量的技术。相比专业摄影师在拍摄过程中使用的各种稳定工具，如三脚架、相机推车等，一个业余拍摄的视频(通常来自没有任何稳定装置的手持设备或者无人机)自然缺乏足够的稳定性[1]。一般而言，稳像过程由以下三个阶段组成：(1)估计原始相机路径；(2)生成新的平滑相机路径；(3)使用生成的平滑相机路径合成稳定的视频[2]。本文完成了以上三个阶段的工作。其中，如何对原始相机路径进行优化是稳像任务的关键，也是本文研究的重点。

现有的稳像技术使用基于像素或关键点跟踪的2D变换模型(如单应性矩阵或仿射矩阵)或者利用运动恢复结构技术(SfM)来估计相机在拍摄期间的运动。然后通过去除相机运动数据中的高频噪声[2-3]，或者采用运动路径拟合的方法[3-4]，生成新的更为平滑的相机路径，从而提高视频的稳定性。

在如何计算最优相机路径的问题上，无论是近来提出的一些新兴稳像技术[5-6]，还是基于SfM的复杂的三维稳像方法[7]，都是直接选用等时间间隔的图像帧来估计并平滑原始相机路径，而忽略了因相机本身的运动速度变化带来的空间间隔的不均匀性。因此，本文试图解决相机运动速度与视频抖动之间的相关性问题。经典的稳像算法[4,8]通过将原始相机路径分为静止、线性或抛物线的运动分段来获得最优路径。本文算法则是依据相机在不同路径段上的运动速度，采用多分辨率重采样的方法，为相机在整个拍摄过程中的路径移动找到其最佳的匹配速度，保证图像帧采样在空间分布上的均匀性，进而达到稳定视频的目的。

本文算法采用流式处理方式，沿着原始相机路径移动一个滑动窗口；对窗口内的原始图像帧进行多分辨率重采样，计算其帧间变换参数；使用最小二乘多项式拟合方法平滑各个相机路径，选择其中与原始相机路径的均方误差不超过阈值且最为平滑的结果作为最优解。而后基于最优相机路径，重新渲染得到最终稳定的视频。该算法保证了在剧烈抖动情况下的良好平滑效果，同时能够去除人在行走过程中产生的低频抖动；可以做到实时处理，在不需要用户交互的情况下自适应地完成视频稳像任务。

1 基于滑动窗口的多项式路径平滑算法

对于以下的讨论，本文假设已经(通过特征点匹配[9]或光流跟踪[10]的方法)计算了在每个时间点t=1,2,…,N的相机变换矩阵Tt(可以表示为6自由度的仿射变换)。设置第一帧图像为参考帧，其对应的相机位置为初始点，在一系列的原始图像帧l1,l2，…，lN中，相邻帧对(lt-1,lt)由变换矩阵Tt相关联。每一帧lt定义的离散相机路径为C(t)，可由矩阵乘法迭代计算：

Ct+1=CtTt+1⟹Ct=T1T2…Tt

(1)

1.1 滑动窗口

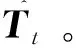
(2)

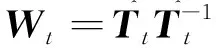
1.2 多项式平滑算法

本文对滑动窗口内的相机路径进行多项式平滑优化，其基本思想是用前后m个不同权重的相机位姿X=(Xt-m,…,Xt,…,Xt+m)T来更新当前位姿Xt。其中，原始相机位姿Xt=(xt,yt)T，可由前后帧对的变换矩阵Tt获得。例如，Tt为6自由度的仿射变换，可得相机位姿的迭代计算公式为：

(3)

对于拟合的多项式次数为n的情况，w个原始相机位姿组成的方程组表示如下：

(4)

更简单地，将(4)式写成矩阵形式：

X=A*ω

(5)

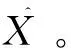
在多项式拟合的过程中，窗口大小w和多项式次数n为两个重要参数，其不同取值直接影响到权重矩阵ω的计算结果，进而决定相机路径的平滑效果和时间耗费。在2.2节最优路径选择中对于次数n的选择会有更详细的说明。

2 基于自适应速度选择的路径优化算法

多项式平滑算法具有参数少、速度快的优点，可以完成对相机路径粗略的去抖动处理。但由于参数n是用户指定的，只能提供单一尺度下的路径平滑，对于在各路径段存在显著速度差异的视频流则不能提供自主、鲁棒的稳像结果。

依据人的视觉感官经验，相机本身的运动速度与视频的稳定程度之间存在着一定的关联。确切地说，沿着相同的方向拍摄同一场景，以更快的速度移动相机可以减轻高频噪声对相机路径的影响，使得相机的运动路径更加平滑。因此，本文通过改变滑动窗口内原始图像帧的采样频率，变相地达到调整相机在各阶段运动速度的目的，实现全局速度自适应的路径平滑。

2.1 图像帧重采样

在大小为w=2m+1的滑动窗口内，对相机位姿进行间隔帧数为γ=1,2,…,w的均匀重采样，即采样频率调整为γ(原始采样频率为1)，更新原始相机位姿集合：

Xγ=(Xt-kγ,…,Xt-γ,Xt,Xt+γ,…,Xt+kγ)T

(6)

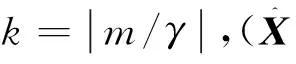
2.2 最优路径选择

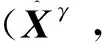
(7)

对于不同的采样频率γ={1,2,…,w}，可以计算得到平滑路径集合P={P1(t),P2(t),…,Pw(t)}，同时计算对应的均方误差E={e1,e2,…,ew}。依据实验结果，增大γ意味着相机以更快的运动速度通过了指定路段，运动路径的平滑程度随之提高。但与此同时，平滑后的轨迹误差相应增大，即与原始路径的偏离程度也是递增的。因此，本文设置最大阈值ε，在满足e≤ε条件的所有优化相机路径集合中，选择其中最平滑的一条作为最优路径：

γopt=max{γ|eγ≤ε}

(8)

图1总结了基于自适应速度选择算法的路径平滑过程。

图1 算法流程图

需要补充的是，在利用多项式平滑算法计算优化相机路径的过程中，次数n的选取是随采样频率γ的增大而递减的。1.2节中提到，n的取值直接影响到相机轨迹的平滑程度，现试从相机运动的物理学角度具体分析,如表1所示。

表1 拟合路径形态与n取值关系

表1中，c、a、a′为常数项。图2所示的实验结果同样表明选用更高次数项的拟合结果所对应的相机路径形态更加复杂，与原始数据吻合程度高但路径的平滑程度低。因此，本文在对重采样后的相机路径进行多项式平滑的过程中，对n的选择加以约束：γ+n≤5,γ<5且n=1,γ≥5，保证了采样频率γ大的路径对应的拟合结果更为平滑。

3 视频稳像系统

本文通过以下步骤来实现视频稳像：(1)估计帧运动变换Tt；(2)利用自适应速度选择算法计算最佳路径Pt；(3)通过Wt形变来输出稳定视频。

对于运动估计，本文使用金字塔Lucas-Kanade跟踪特征[10]，应用RANSAC算法来估计平移变换，只保留与估计变换一致的阈值距离(小于两个像素)，从而有效地排除异常点。

对于将原始视频从新的平滑相机路径中重新渲染出来的问题，本文采用最简单的鲁棒方法，即指定一个预定义比例的裁剪窗口，将原始相机路径C(t)和平滑后的相机路径P(t)之间的转换矩阵Wt应用到裁剪窗口中，使得原始视频重投影到最优相机路径拍摄的位置，从而输出最终的稳定视频。其中，转换矩阵Wt的计算如下：

(9)

4 实验结果

为了验证算法的有效性，首先基于最直观的视觉体验角度，本文选择L1最优路径方法[4]中研究的“Fan-Cam”抖动视频来表现视频稳像的结果。图3选取了原始视频中的第1、17和340帧，可以明显看出在水平方向上有着明显的抖动。图4则展示了稳像后的对应结果，水平方向上的抖动被有效地去除了。

图2 对原始相机路径(实线)进行不同多项式次数(n=1,2,3,4)的路径拟合结果(正方形)

图3 原始图像帧

图4 稳像后图像帧

本文算法除了抑制明显的高频抖动之外，还能够消除因步行过程中拍摄视频所产生的低频失真，具体可通过调整设定的阈值ε的取值实现。如图5中y轴方向上的运动可用常量或匀速路径代替。

图5 在x、y轴方向上的优化相机路径

将本文算法与卡尔曼滤波、粒子滤波和L1最优路径方法进行比较，对比算法的稳像效果及实时处理的能力。实验中，选择文献[1]中提供的视频集(http://web.cecs.pdx.edu/～fliu/project/subspace_stabilization/)进行稳像处理，利用峰值信噪比(PSNR)评估算法的去抖效果，PSNR值越高表明稳像效果越好，结果如表2所示。四种稳像算法处理后的单帧平均用时如表3所示。

从表2中可以看出，原始视频存在明显的抖动，本文算法在对比实验中对视频的平滑处理效果显著。由表3显示的单帧图像处理时间看出，本文算法具有良好的实时性，在处理时间上均优于滤波算法和L1最优路径算法。

5 结论

本文提出了一种基于自适应速度选择的路径优化算法，实时地对视频完成去抖动处理。实验结果表明，本文算法具有良好的稳像效果，不仅能够抑制明显的高频抖动，对于行走产生的低频抖动也能有效地去除，保持了视频拍摄的原始意图。本文在输出稳定视频时有效地裁剪了帧，其大小是预定义比例的，在今后的工作中，希望能够自动计算最佳裁剪的大小。同时，对于仿射变换不能模拟非线性帧间运动所导致的残留摆动，也是下一步工作的重点。

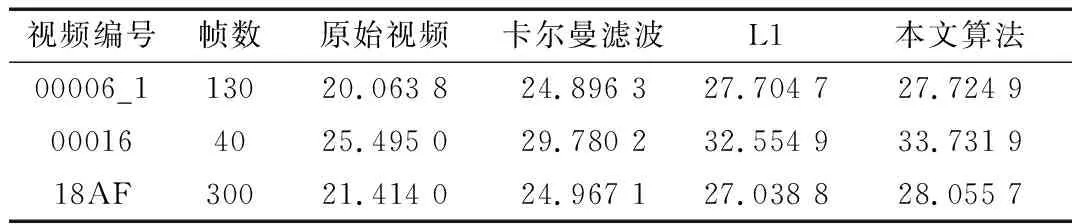
表2 稳像算法处理后视频PSNR平均值比较(dB)

表3 稳像算法处理单帧图像平均用时比较(ms)