Gd19+离子双电子复合速率系数的理论研究

符彦飙,魏二龙，田 瑞，马德全

(1.西北师范大学物理与电子工程学院,甘肃省原子分子物理与功能材料重点实验室,甘肃兰州 730070; 2.西北师范大学与中科院近代物理研究所极端环境原子分子物理实验室, 甘肃兰州 730070)

近年来,由于诸如磁约束聚变等应用研究的需要,基组态为4d/4f壳层的复杂结构离子的双电子复合(DR)过程的研究被广泛关注[1-8].Schippers等[1]对基组态为4p64d104f13的Au20+离子进行了实验测量,观察到了明显的DR特征.Balance等[2]做了和该实验结果符合很好的理论计算.同时Badnell等[3]利用AUTOSTRUCTURE程序,对基组态4d104f8结构W20+离子的DR过程进行了研究,并和Schippers等[4]在重离子储存环上的实验结果做了比较.由于极真空紫外光刻光源的研究,激光烧蚀产生的Sn和Xe离子因其发射的N-O壳层跃迁线在13.5 nm附近的极紫外光谱在MO/Si多层镜面有极高的反射率,其DR过程成为了研究的热点[5-8].2008年,Song等[5]对Xe10+离子的4d电子激发到4f和5p壳层的双电子复合过程进行了细致的研究；2009年,Safronova等[6]利用Hartree-Fork-Relativistic(HFR)和多体微扰方法详细研究了类钯Xe8+离子的激发能量、辐射跃迁速率系数、自电离速率系数、双电子伴线和双电子复合速率系数.本课题组[7-8]对Sn10+和Sn12+离子的双电子复合速率系数也进行了详细的计算研究.为寻求更短波长的极真空紫外光刻光源,Gd发射的6.xnm附近的N-O壳层跃迁线受到关注[9-10].由于这些跃迁涉及到多个开放的4d壳层电子,它们与其他壳层的电子强烈耦合可以形成非常复杂的近简并能级,这些能级之间的跃迁形成的谱线将变得非常复杂,并且相互重叠,形成所谓的“不可分辨的跃迁峰(UTA)”.这就使得对这些谱线的分析和辨认变得非常困难.因此,必须对有关离子态的能级结构和跃迁光谱特性进行详细的理论和实验方面的分析研究.当等离子体密度很高时,电子与原子碰撞频率比辐射跃迁速率快得多,以至于在等离子体中形成局部热动平衡(LTE),此时原子数密度分布由统计方法给出的沙哈(Saha)方程决定.而在极低电子密度情况下,碰撞激发的速率比辐射衰变的速率小得多,并且不同电离度原子基本都处于基态,它们的分布用碰撞辐射模型决定.在中等电子密度情况下,有不少原子分布在激发态上,对于这些原子数密度分布,不仅要计算不同电离度原子的丰度,还要计算所有重要激发态的占据率,这就必须求解包含各种电离与复合、激发与退激发过程的速率方程.而对于基组态为4d/4f壳层的复杂结构离子的DR速率系数,经验公式和从头计算的结果相差较大[11]，而细致的从头计算比较复杂耗时，所以在等离子体谱的模拟中往往不考虑DR速率系数.然而在很多情况下其DR速率系数大于辐射复合(RR)以及三体复合(TBR)速率系数[7，11-13].因而,精确的复杂结构离子DR过程的相关参数是非常重要的.目前国内外对于复杂结构重离子DR速率系数的计算,往往忽略辐射跃迁至自电离态且随后级联退激(DAC)的贡献.Li等[11-12]研究了外壳层为4d电子的Gd19+, Gd20+离子的DR过程,在5 eV～50 keV的温度区域之外,DR速率系数大于RR和TBR速率系数,DR速率系数在EUV光刻光源,激光产生的Gd等离子体的谱模拟中极其重要.Meng等[14]计算了基组态为3d9结构的Au52+离子DR过程,分析得到DAC效应对于总DR速率系数在1 000 eV处有10%的增大.笔者等[13]对Au34+离子DR过程理论研究中,DAC的最大贡献为12%.为得到在更为精确的类铑Gd19+离子DR过程的相关参数,细致考察包括DAC在内的各类效应对复杂结构离子DR过程的影响,文中利用基于全相对论组态相互作用理论的Flexible atomic Code(FAC)[15]程序对Gd19+离子DR过程进行细致的理论研究.

1 理论方法

Gd19+离子由基态i俘获一个自由电子,形成中间双激发态j,再辐射退激发到f的双电子复合过程为[13]

其中,**表示中间双激发态j,*表示辐射跃迁末态f．由初态i经过双激发态j再到所有辐射跃迁末态f的DR速率系数为[13]

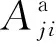
(3)

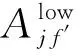
2 结果与讨论

基组态为4d壳层离子的DR过程比较复杂,尤其是考虑DAC效应的精细计算需要耗费大量的资源.为在有限的资源下忽略不重要的贡献,得到较为理想的结果,以基态作为初态,首先详细分析各种效应及通道对Gd19+离子DR过程的贡献,进而得到相对精确的总DR速率系数.

2.1 Gd18+离子辐射跃迁比较

表1给出了Gd18+离子辐射跃迁波长的比较,其中,RPTMP和实验为Ivanova[16]展示的理论和实验结果.文中考虑组态相互作用时,辐射跃迁末态考虑4p64d10,4p64d95s和4p54d104f间的相互作用,辐射跃迁初态考虑4p64d94f,4p64d95p,4p64d95f,4p54d94f2,4p54d94f5p,4p54d94f5f间的相互作用.Cowan为文中在单组态下利用Cowan程序计算得到的结果.由表1可以看到,和RPTMP的计算比较,单组态下本文计算得到的结果最大偏差为1.05%,最小为0.03%.考虑组态相关互作用后最大偏差为2.06%,最小为0.04%.Cowan程序计算的结果和单组态下FAC程序计算结果的偏差在0.25%～0.88%.和实验比较,单组态下的偏差分别为0.17%和2.66%.RPTMP的结果要好一点,偏差分别为0.02%和1.63%.从图1也可以看到,单组态下的结果和RPTMP、实验以及Cowan的结果符合的比较好.

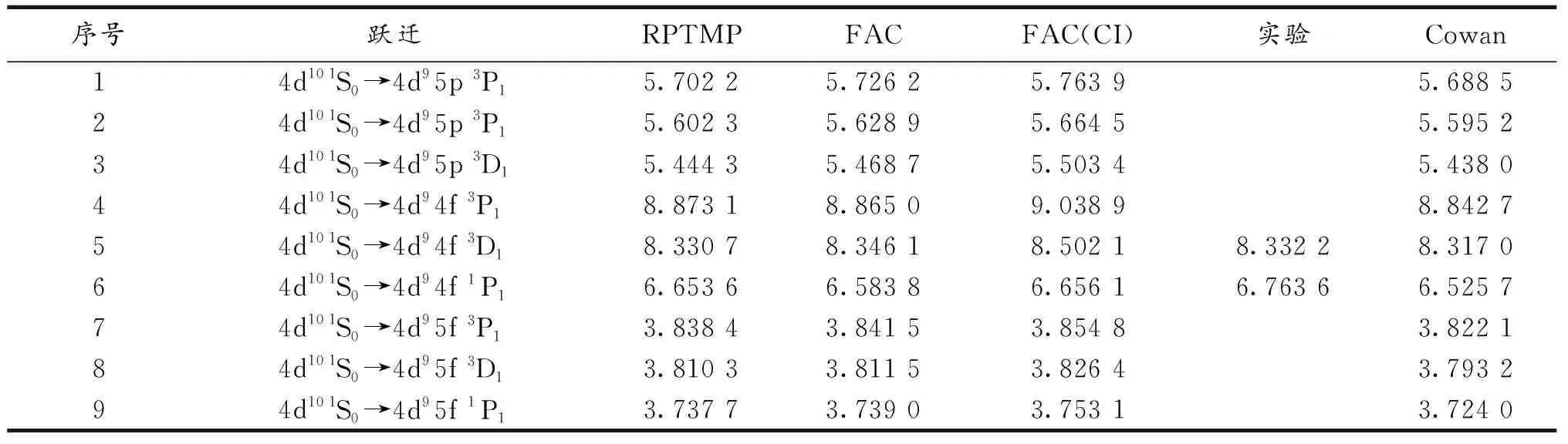
表1 Gd18+离子辐射跃迁波长(nm)比较

2.2 激发和辐射通道

图2给出了j=(4s24p64d9)-14l10f的DR速率系数.可以看出,4d电子激发的DR速率系数最大,4s电子激发的DR速率系数最小.考察曲线峰值附近,4p电子激发的DR速率系数为4d电子激发的8.4%,其对总DR速率系数的贡献不可以忽略.4s电子激发的DR速率系数为4d电子激发的0.8%,其贡献在本文接下来对DR速率系数各类效应的分析讨论以及总DR速率系数的计算中予以忽略.

图3给出了j=(4p64d9)-1nl10l′,n=4,5,6的DR速率系数.由图3(a)可见,在全温度区域内,对于4d电子激发,n=4的DR速率系数最大,n=6的最小.n=5的DR速率系数峰值仅为n=4峰值的5.4%.而n=6的DR速率系数峰值仅为n=4峰值的1.3%.图3(b)为4p电子激发的DR速率系数，由图3(b)可见,n=5的DR速率系数峰值为n=4峰值的42.4%.n=6的DR速率系数峰值为n=4峰值的10.6%,n=6的DR速率系数峰值为n=5峰值的26.9%.4p电子激发n=5,6的贡献相对于4d电子激发的n=5,6的贡献要大得多,原因在于4p54d1010l′中4d为满壳层,高壳层电子无法向4d跃迁,导致中间双激发态4p54d1010l′的贡献降低.从图1可知,4p电子激发的DR速率系数峰值处为4d电子激发的8.4%,相应的(4p64d9)-16l10l′对总DR速率系数的贡献应该在1%以下.并且随着n的增大,相应的贡献急剧降低,故而在计算中,忽略n>6的贡献.

图1 Gd18+离子辐射跃迁波长

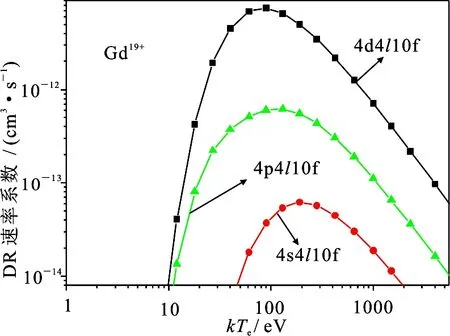
图2 4s,4p,4d电子激发对DR速率系数的贡献

图4给出了j=4d84f10f,辐射跃迁末态f=4d910f,4d94f,4d84f5l″,4d84f6l″,4d84f7l″,4d84f8l″的DR速率系数.曲线4为辐射跃迁至4l壳层,曲线5为辐射跃迁至4l,5l壳层的DR速率系数.两者之间在峰值处有6.6%的差异.曲线6为辐射跃迁至4l～6l的DR速率系数,和曲线5有1.3%的差异.曲线7为辐射跃迁至4l～7l的DR速率系数,和曲线6有0.03%的差异.曲线8包括了辐射跃迁至4l～8l的贡献,可以看到基本上和曲线7重合.考虑到不同的中间双激发态的辐射跃迁差异,我们的计算中忽略辐射跃迁至7l以上壳层的贡献.

图3 j=(4p64d9)-1nl10l′,n=4,5,6的DR速率系数

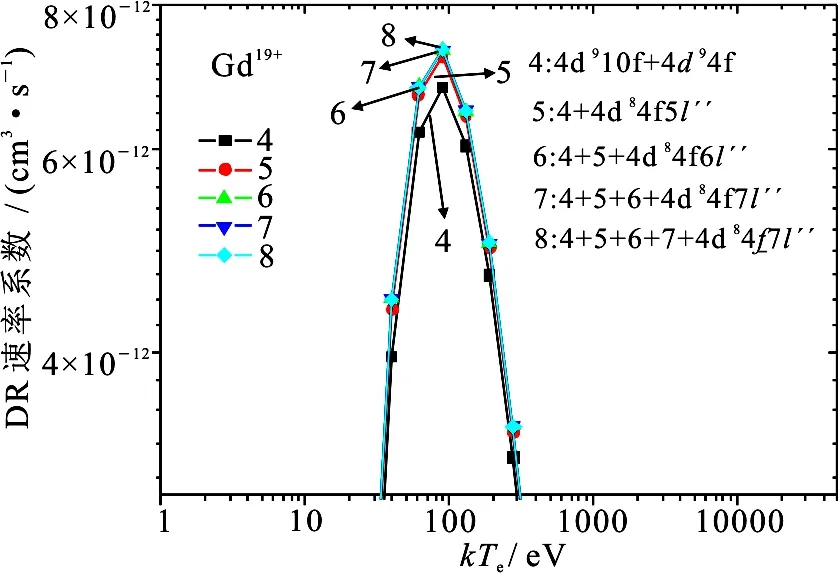
图4 辐射跃迁至不同壳层的DR速率系数

2.3 级联退激的影响

图5给出了3种辐射跃迁末态类型的DR速率系数.辐射跃迁根据前面的分析,考虑跃迁至4l～7l壳层.图5中,RS+NRS表示中间双激发态的辐射跃迁考虑了共振稳态跃迁(RS)和非共振稳态跃迁(NRS)；DAC表示在考虑NRS+RS的基础上,考虑了辐射跃迁至可自电离态及其随后的级联退激；NDAC表示考虑和DAC相同的第一步辐射跃迁,但不考虑随后的级联退激.可以看到各种类型的辐射跃迁的DR速率系数相等.原因是其辐射末态大部分都处于电离限以下.在Li等[11]对Gd18+离子电离限附近双激发态能级的计算中,4d84f2,4d84f5l都处于电离限下,辐射跃迁到这些能级的都为NRS跃迁.图5(b)中130 eV温度处曲线DAC的DR速率系数为RS+NRS的1.5倍,并且随着温度的增加,DAC的贡献逐渐增大,在50 000 eV处为2.2倍.在Li等[11]计算的能级图中,4d85f5l的能级都处于电离限以上,相应的辐射跃迁到这些能级上的级联退激对DR速率系数都有影响.130 eV温度处曲线NDAC的DR速率系数是DAC的2倍,说明中间态的第一步辐射跃迁末态的Auger几率比较大,其平均分支比小于0.5,所以计算中需要考虑第一步辐射跃迁末态分支比的影响.在Li等[11]计算的能级图中,4p电子激发的双激发态相对于4d电子激发,有更多的双激发态处于电离限以上,其DAC效应的影响会更大一些.

2.4 DR速率系数随高n电子轨道角动量的变化

图6给出了DR速率系数随高n电子轨道角动量的变化,其中j=4d8nln′l′,n=4～6,n′=4～23,l′=0～11.可以看到在全温度范围内,l′=g的贡献最大.在温度小于10 eV的低温区域,主要为l′=g,d,f,p,s,h的贡献.这些轨道在1 eV附近有较大贡献的原因是双激发态4d84f6l,4d84f7l,4d85s5l,4d85p5l,4d85d5l,4d85s6l,4d85p6l的许多能级处于电离限附近.而由(2)式可以看到,DR速率系数和(kTe)-3/2exp(-Eji/kTe)相关,1 eV附近的共振能Eji在小于10 eV的低温区域会有较大的DR速率系数.在温度大于20 keV的高温区域,主要是l′=g,h,i,f,d,k,p的贡献.l′>8的DR速率系数随着l′的增大,规律性递减.l′=o的贡献最小,其DR速率系数的最大值为l′=g的0.01%.计算中忽略掉l′>11的贡献是合理的.

图5 3种辐射跃迁末态类型的DR速率系数

图6 DR速率系数随高n电子轨道角动量的变化

Fig 6 The dependence of the DR rate coefficients on the orbital angular momentum of high-nelectron

2.5 总DR速率系数

图7给出了Gd19+离子DR,RR,TBR速率系数.曲线DR-DAC-4d,DR-DAC-4p,DR-DAC,DR-RS+NRS以及DR-NDAC为j=(4p64d9)-1(n=4～6,n′=4～23),利用FAC程序从头计算得到.DR-DAC-4d,DR-DAC-4p分别为4d和4p电子激发考虑了DAC效应的DR速率系数.由图可以看到,在全温度范围内,4d电子激发的贡献大于4p电子激发.4p电子激发的DR速率系数是4d电子激发DR速率系数的48%～72%,所以内壳层4p电子激发的贡献非常重要.通过曲线DR-DAC和DR-RS+NRS的比较可以看出,在温度Te<20 eV区域,DAC效应对DR速率系数没有影响,在90 eV处，DAC使DR速率系数增大了1.5%.之后随着温度的增高,影响逐渐增大.在280 eV处,总DR速率系数增大3.3%,在50 000 eV处增大4.1%.如果考虑高里德堡电子辐射跃迁而不考虑级联退激(曲线DR-NDAC),在40 eV处对DR速率系数(曲线DR-DAC)增大4.5%,并且随着温度的升高,影响逐渐增大,在50 000 eV处增大到70.7%.综合以上分析,说明级联退激中,Auger退激的速率比较大.曲线DR-Ref为Li等[11]计算的未考虑DAC效应的DR速率系数,同时RR和TBR速率系数也采用Li等[11]的数据.可以看到，在温度大于200 eV区域和曲线DR-RS+NRS非常接近.在50 000 eV处,两者的差异为0.2%.曲线DR-DAC(n′=24～1 000)为通过n′=23的数据按照(3)式外推得到的n′=24～1 000的DR速率系数.DR-DAC-total(n′=4～1 000)为总DR速率系数.外推部分在40 eV处对于总DR速率系数的贡献为3%.在温度大于300 eV区域,外推的贡献和4p电子激发不加外推部分的总DR速率系数相当(总DR速率系数的22%),在50 000 eV处为25.8%.而总DR速率系数在全温度范围都大于RR和TBR速率系数.可见DR过程对于等离子体离化态分布和能级布居以及光谱模拟极为重要.

曲线DR-DAC-4d和DR-DAC-4p分别为4d和4p电子激发的考虑了DAC效应的DR速率系数;曲线DR-DAC-4d,DR-DAC-4p,DR-DAC,DR-RS+NRS以及DR-NDAC为j=(4p64d9)-1(n=4～6,n′=4～23)的DR速率系数.

图7 Gd19+离子DR,RR,TBR速率系数

Fig 7DR,RR and TBR rate coefficients for Gd19+ions

3 结论

详细研究了Gd19+离子的DR过程.以基态作为初态,考察了激发、辐射通道,DAC效应对DR速率系数的贡献,以及DR速率系数随高n电子轨道角动量的变化.其中,4s电子激发的贡献可以忽略.4d电子激发至7l及更高壳层的贡献可以忽略,辐射跃迁至8l及更高壳层的贡献可以忽略.高n电子轨道角动量l′>11的贡献可以忽略.在温度kTe<20 eV区域,DAC效应对DR速率系数无影响,在90 eV处DAC使DR速率系数增大了1.5%.之后随着温度的增高,影响逐渐增大.在280 eV处,总DR速率系数增大3.3%,在50 000 eV处增大4.1%.由于级联退激中Auger退激速率较大，考虑高里德堡电子辐射跃迁而不考虑级联退激,在40 eV处对DR速率系数有4.5%的增大,并且随着温度的增大,影响逐渐增大,在50 000 eV处增大到70.7%.对DR,RR,TBR速率系数做了比较,在全温度范围DR都大于RR和TBR速率系数,相应的DR过程对于等离子体离化态分布和能级布居以及光谱模拟都极为重要.为方便应用,分别对基态和第一激发态作为初态的总DR速率系数进行了参数拟合,拟合公式为

对于基态作为初组态的DR速率系数拟合结果,在温度为1 000 eV处,拟合偏差为1.54%,1 500 eV处为1.6%.其他数据点处的拟合偏差都小于1.0%.对于第一激发态作为初组态的DR速率系数拟合结果,在温度为1 000 eV处,拟合偏差为1.3%,1 500 eV处为1.1%,其他数据点处的拟合偏差都小于1.0%.

表1 Gd19+离子DR速率系数参数拟合