基于形状曲线的机载LiDAR点云汽车类型识别
2018-10-22金国清
金国清
(中铁第五勘察设计院集团有限公司,北京 102600)
1 概述
基于机载LiDAR点云的汽车类型识别技术可应用于数字高程模型生产[1,2],城市停车管理[3],交通管理[4]以及数字城市和智慧城市[5]等。目前,基于机载LiDAR点云的相关研究主要集中于汽车提取,即判定点云块是否为汽车,对汽车类型判定[6]的研究较少,以下的研究对象仅考虑三厢车(Sedan)、掀背车(Hatchback)、越野车(SUV)和厢式货车(VAN)等四种汽车类型。
目前的研究中,多根据汽车点云分块俯视图的长和宽等几何特征信息来判定其是否为汽车[7-8],而这些几何特征信息并非根本性指标,判断的准确率有限,且不能对目标汽车类型进行判断。考虑到汽车点云的侧视图中汽车形状曲线与汽车类型密切相关,不同类型的汽车形状具有显著差异,可用为汽车点云分块判断的依据。这个方法的核心问题就是如何判断两个汽车形状(侧视图)的曲线是否相似。由于汽车形状曲线是二维曲线,因此该问题的本质就是如何评价两条二维曲线是否相似。目前在图像配准、目标检测识别领域内常采用Hausdorff距离[9],离散Fréchet距离[10-11],动态时间规整(Dynamic Time Warping,DTW)距离[12]等几种离散点集的相似度度量指标。
2 基于形状的点云汽车类型识别方法
首先采用布料模拟滤波(Cloth Simulation Filter, CSF)将点云分为地面点和非地面点。在非地面点云中,采用空间邻域分析(CCA)方法进行分块,然后根据每个小块的长度、宽度和高度,剔除所有汽车尺寸范围外的点云分块,最后对每个点云分块建立其形状曲线。
得到该形状曲线之后,就可以与标准汽车形状库中的形状曲线进行比较,计算相似度指标。如果最小的相似度指标小于设定的阈值,那么对应的标准汽车形状的类型就是该点云的汽车类型,否则判定为非车目标(见图1)。

图1 汽车类型识别方法
2.1 汽车形状构建方法
根据点云构建汽车形状曲线是该方法中的关键步骤之一,其距离建立过程如下。
(1)将汽车点云分块的激光点垂直投影到水平面上,建立该分块的最小外包矩形,作为汽车的位置标定。
(2)取矩形的短边中点连线作为基准线,取过该基准线的竖直面作为基准面。考虑到激光点云为离散的不规则点云,在基准面左右设置缓冲区。缓冲区厚度一般为2~3倍的平均点间隔(本文设置为0.6 m)。
(3)将缓冲区中的各点水平投影到基准面上,按照从起点到终点的顺序进行排序,并按照0.3 m的间隔进行重采样,得到一个间隔均匀的离散曲线,作为汽车点云形状(见图2)。
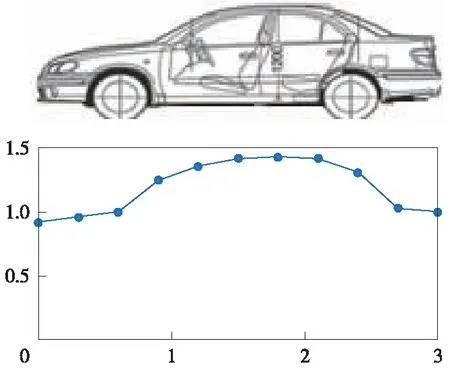
图2 汽车形状曲线
2.2 汽车形状相似度指标计算
在该方法中,相似度指标的选择是汽车类型识别方法的核心,是影响汽车类型判别的关键。考虑到汽车形状为二维曲线,在模式识别、人工智能领域内对二维曲线的相似性有很多相关研究。以下选择Hausdorff距离、离散Fréchet距离、DTW规整距离三种相似度评价指标。Hausdorff距离广泛应用于图像配准、目标识别与检测[9];离散Fréchet距离可用于生物特征识别[10]、地图匹配[13];DTW规整距离则主要应用于语音识别[12]。
(1)Hausdorff距离
Hausdorff距离作为衡量点集之间相似度的一种指标,不考虑点之间的连接关系,仅考虑点的位置。对于任意两个有限点集P={p1,p2,,pm},Q={q1,q2,,qn},两者之间的Hausdorff距离可定义[14]为
DH(P,Q)=max(dh(P,Q),dh(Q,P))
(1)

DH(P,Q)可用于判断P,Q的相似性,其值越小,则P,Q形状越相似;反之亦然。
(2)离散Fréchet距离
离散Fréchet距离是衡量曲线相似度的一种指标,在考虑点位置的基础上,还考虑了点的排列,其定义[15]如下:
P和Q分别为m和n个点组成的多边形链,令σ(P)=(p1,p2,,pm)
σ(Q)=(q1,q2,,qn),则有
L={(pa1,qb1),(pa2,qb2),,(pak,qbk)}
(2)

(3)
则P和Q的离散Fréchet距离定义为
(4)
DF(P,Q)可用于判断P,Q的相似性,其值越小,则P,Q形状越相似;反之亦然。
(3)DTW规整距离
DTW算法基于动态规划的思想,可计算两个相关不同长度模板之间的相似性。假设有参考模板和测试模板分别为P={p1,p2,,pm}与Q={q1,q2,,qn},其中模板的分量pi(0 (5) DDTW(i,j)可用于判断P,Q的相似性,其值越小,则P,Q形状越相似;反之亦然。 实验数据采用2010年采集于荷兰Utrecht市某商业中心的机载LiDAR点云数据,点密度为20~30 pts/m2,区域范围约200 m×120 m(见图3)。汽车停放于停车场内和建筑周围,部分位于路边,共计263台汽车。 图3 实验数据 在建立标准汽车形状集时,包括了从车头到车尾和从车尾到车头两条形状曲线(见图4)。 图4 标准纵剖面曲线 对点云进行布料模拟滤波(CSF),对分离出来的非地面点进行分块和初步筛选,得到360个候选点云分块(见图5)。对每个分块按照1.1节中的方法构建形状曲线,然后分别利用Hausdorff距离、离散Fréchet距离和DTW规整距离三个指标计算其与标准汽车形状的相似度指标。其相似度阈值分别为0.95,0.95和6.5。 采用人工交互方式确定的汽车类型作为评价依据。这360个候选点云分块共有97个为非车地物目标,263个为汽车。其中厢式货车4台,掀背车184台,三厢车61台,越野车14台(见图5)。 图5 候选点云分块和人工识别结果 采用Hausdorff距离、离散Fréchet距离和DTW规整距离三个不同的相似度评价指标,按照1.2节中的方法来进行汽车类型识别,结果如图6。 图6 采用不同相似度指标的汽车类型识别结果 三种相似度评价指标的汽车类型识别结果及人工识别结果如表1。 山谷到黔州,现重庆彭水苗族土家族自治县,更为偏远荒凉,心情抑郁愤懑,苦闷与悲哀无处不在。如:《答王补之书》:“今者不肖得罪简牍,弃绝明时,万死投荒,一身吊影,不复齿于士大夫矣。”(转引自伍联群《黄庭坚蜀中交游及其对巴蜀地域文化的推动》,《文艺评论》,2011年第4期)《与太虚公书》:“摒弃不毛之乡,以御魑魅,耳目昏塞,旧学废忘,直是黔中一老农耳。”(《黄庭坚全集》,四川大学出版社,第1377页) 表1 汽车类型识别结果 采用准确率、完整性和F值等三个指标[17-19]来对实验结果进行分析。 准确率(Precision) (6) 完整性(Recall) (7) F值(Fscore),是前述二者的调和均值,本文将该指标用作汽车识别性能的总体评价指标。 (8) 其中,在非车目标识别中,tp表示结果判定为汽车且实际为汽车的数量,fp表示结果判定为汽车但实际为非车的数量,fn表示结果判定为非车但实际为汽车的数量;在具体汽车类型识别中,tp表示结果判定为某类汽车且实际为该类汽车的数量,fp表示结果判定为某类汽车但实际为其它类型汽车或者非车的数量,fn表示结果判定为其它类型汽车或者非车但实际为某类汽车的数量。 (1)非车目标识别结果分析 候选点云分块中非车目标的准确判断是汽车类型识别工作中的重要内容,三种相似度评价指标对非车目标的识别结果见表2。 表2 非车目标识别精度比较 三种相似度指标判别结果的准确率基本相当,Hausdorff距离准确率稍优,DTW规整距离和离散Fréchet距离的完整性均大于98%,基本能将所有非车目标判断出来,Hausdorff距离的完整性稍低于其他二个相似度评价指标。 从算法性能的总体评价指标(F值)来看,三种相似度评价指标中DTW规整距离对非车目标的识别效果稍好。 (2)具体汽车类型识别的准确性分析 四种类型汽车中,厢式货车仅有4辆,数据量不足,以下不对厢式货车进行具体汽车类型识别的准确性分析。就其它三种车型而言,不同的相似度评价方法对具体汽车类型的识别结果如图7。 图7 不同相似度指标下的不同汽车类型识别 从准确率看:对掀背车三种相似度指标基本相当;就三厢车而言,DTW规整距离的准确率最高;就越野车而言,Hausdorff距离与离散Fréchet距离结果一致,DTW规整距离较高。 从完整性看:对于掀背车,DTW规整距离的结果完整性为82.1%,明显高于其它两种相似度指标;就三厢车而言,三种相似度指标完整性一致,其中Hausdorff距离稍差;就越野车而言,DTW规整距离的完整性高出其它两者14.3%。 从算法性能的总体评价指标(F值)看:对掀背车,DTW规整距离的F值高出其它两种指标12.4%,就三厢车而言,DTW规整距离的F值高出Hausdorff距离12.7%,高出离散Fréchet距离15.1%,本试验区越野车数量较少,三种相似度评价指标得到的F值结果基本相当。总体而言,DTW规整距离的总体评价指标最优,F值平均为72.9%。 对于具体汽车类型识别而言,采用DTW规整距离作为相似度指标,算法效果最优。汽车形状可看作一个时间序列,其中汽车长度等效于时间,汽车高度可视为时信号。DTW规整距离只受高度和形状影响,不受长度影响。因此,对同类汽车可能存在长度不一的情况适应性最好,识别效果最优。 基于汽车形状曲线的机载点云汽车类型判别方法能够有效判定候选点云分块中的非车目标以及汽车的具体类型。从总体评价指标(F值)来看,DTW规整距离作为相似度指标效果最好。 对于非车目标的识别,采用DTW规整距离作为相似度算法的总体性能指标最优。对于掀背车,越野车和三厢车等三种具体车型识别总体性能指标,DTW规整距离均优于Hausdorff距离、离散Fréchet距离这两个指标。3 试验
3.1 实验数据



3.2 汽车类型识别结果

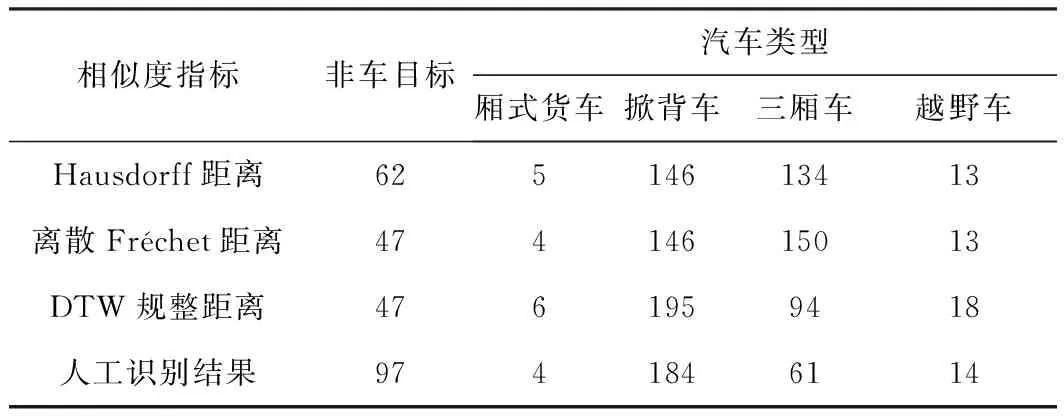
3.3 汽车类型识别结果分析

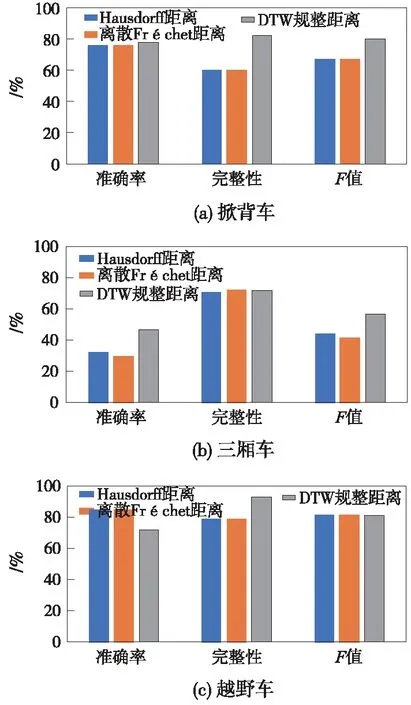
4 结论
