风道出风口结构对客车车内流场影响的研究

2018-10-22宋晓峰黄学章

客车技术与研究 2018年5期

宋晓峰，黄学章

(中南大学能源科学与工程学院，长沙 410083)

车内热舒适性是客车舒适性评价的重要指标之一，主要包括气流组织和温度分布两个方面。气流组织主要是使车内空气的温度、湿度、流速等指标符合人体的舒适性要求，其优劣也将直接影响车内温度分布的均匀度[1-3]。

针对车内气流组织，国外研究人员通过等比例缩小汽车模型进行仿真分析、试验以及数值模拟相结合的方法，研究了送风口速度、位置、回风口布置形式等因素对车内气流组织和热舒适性的影响[4-5]。国内的研究主要集中在运用CFD技术分析空调送风量，送风口数量、位置以及不同送风角度等对车内流场温度场分布规律的影响，并依据仿真结果对风道结构提出相应的优化方案[6-9]。风道出风口射流状态对流场影响的研究则几乎没有。

对此，本文提出一种通过在风道出风口处增设整流挡板来改善出风口射流状态进而优化车内气流组织的方案，并对其高度对车内流场的影响规律进行深入分析。

1 模型的建立与验证

1.1 物理模型

研究对象为某48座空调客车，左右对称布置11排乘客座椅，前端驾驶区设有驾驶员座椅，乘客门侧设有导游座椅。车内几何参数为：长10.17 m，宽2.35 m，高2.68 m。空调系统采用顶部两侧进风、中部回风的布置形式，风道上对应每排座椅处都设有上、中、下3个出风口(靠近走廊的出风口定义为上出风口)。由于客车在横向方向具有较强的对称性，取该车内左侧作为研究对象，并对其结构进行必要的简化。客车车内模型如图1所示，定义客车长度方向为纵向，宽度方向为横向。

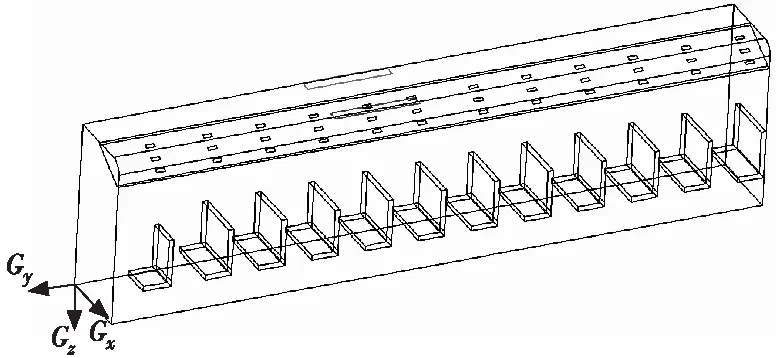
图1 客车车内几何模型

1.2 数学模型

空调客车车内的气流运动属于典型的湍流运动，已有相关研究表明，采用k-ε湍流模型对车内流场进行模拟与实际工况能够较好的吻合[10]。因此，本文采用标准的k-ε湍流模型，由连续性方程、动量方程、湍动能方程(k方程)、湍动能耗散方程(ε方程)构成封闭的方程组，对车内流场进行数值计算。其通用形式[11]为：

(1)

式中各参数取值及含义见参考文献[11]。

1.3 边界条件

客车空调系统气流入口采用速度入口边界条件。出口采用压力出口边界条件。结合现场测试数据，设定入口流速大小为1.5 m/s，出口压强为-25 Pa。

1.4 模型验证

为了验证计算模型的准确性，基于上述计算模型和边界条件进行仿真计算，将计算所得的风道出风口风速与实际用风速仪测试所得的(测量3次求平均值)进行对比分析，对比结果见表1。由表1可知，风道出风口速度呈现出风道前部误差小、后部误差随离顶部进风口距离增加而增大的趋势。这是由于实车风道内后部布置有从顶部进风口下来的空调蒸发器的冷媒媒管，对风道内的流场造成了一定的影响，而在建模过程中忽略了此影响，引起误差的增大。出风口速度的测试数据与模拟数据误差在8%以内，且变化规律一致，证明该仿真模型合理可靠，其他的因素分析可基于该模型进行。

表1 风道出风口风速对比表

2 风道出风口整流挡板结构的提出

由原结构仿真结果可见，风道出风口所对应的车内纵截面上流场分布紊乱，水平截面与横截面上的速度梯度变化较大，在座椅区域流速已趋于0。图2为车内不同截面速度分布云图，显示车内气流组织不理想，存在较大改善空间。究其原因，是由于风道出风口处风速存在较大的纵向分速度，不同风口喷出的射流存在严重的交互影响，虽然这在一定程度上会增加车内流场的湍流度，有利于冷热气流混合，但车内横截面方向上的分速度被严重削弱，并且会导致车内流场出现大量流动“坏区”甚至“死区”。就整体而言，对车内的气流组织是不利的。为了减小风道出风口射流的纵向分速度，本文提出一种在风道出风口处增设整流挡板的方案，整流挡板结构及装配如图3所示。

取上、中、下列整流挡板高度分别为30 mm、45 mm、45 mm建立模型，以上述边界条件进行仿真计算，结果如图4所示。与图2对比可见，风道出风口增加整流挡板后，风道出风口处风速的纵向分速度和车内纵、横截面上的流场均匀性得到明显改善，说明通过增加整流挡板来改善车内流场的方案是可行的。

(a) 出风口处纵截面(b) 距地板1.4 m处水平截面(c) 乘客区横截面

图2 车内不同位置速度分布云图

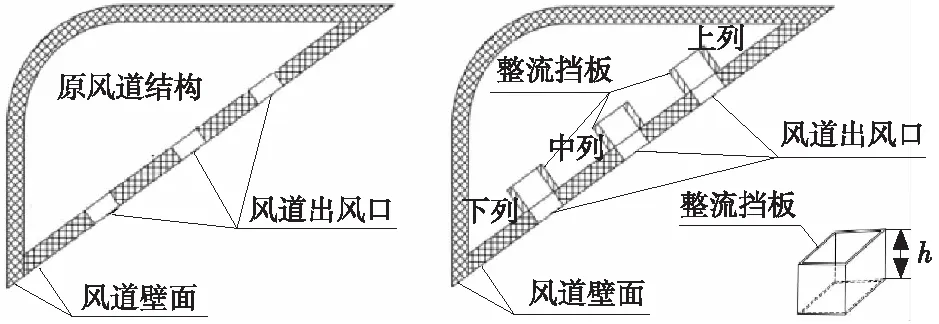
图3 整流挡板结构及装配图

整流挡板置于风道内部，对风道内流场具有扰乱作用。如果设计过高可能引起局部出风口风速不达标，过低又不能有效降低风道出风口处的纵向分速度，起不到作用。因此取整流挡板高度下限为10 mm，上限为所对应风道处高度的1/3作为研究范围。由于不同的整流挡板高度对车内流场的影响不尽相同，现将影响风道出风口处风速的整流挡板高度归纳为上、中、下3列高度，即每列出风口的整流挡板高度一致。

(a) 出风口处纵截面(b) 距地板1.4 m处水平截面(c) 乘客区横截面

图4 车内不同位置速度分布云图

3 挡板高度的影响分析及优化

针对影响风道出风口射流速度的3个参数：上、中、下列整流挡板的高度，在其他参数不变的情况下，研究单一参数对风道出风口射流速度的影响规律。以风道出风口处速度方差及纵向分速度方差作为评判风速均匀度和消除纵向分速度效果的标准，其计算公式见式(2)。

(2)

设定三因素中的一个因素为可变值，另两个因素为固定值，对上、中、下列整流挡板的高度进行取值组合，通过对19组结构(见表2)进行仿真计算，得到上、中、下3列整流挡板高度对风道出风口射流速度的影响规律，如图5所示。

3.1 上列整流挡板对出风口射流速度的影响

从图5可以看出，随着上列整流挡板高度的增加，风道出风口处的纵向分速度逐渐减小；消减作用在10～40 mm之间效果明显，40～50 mm之间显著性变差。这是由于整流挡板形状类似于矩形管，内部流体的运动自由度是唯一的，即整流挡板高度方向，故其具有整流作用，且随着高度增加效果越好，当内部流体流向趋于一致时，效果逐渐减弱。风道出风口风速均匀度随上列整流挡板高度的增加而增加，并逐渐趋于稳定，在高度为[40 mm, 50 mm]之间稳定在0.175 m/s左右。综合分析可得，在研究范围内，上列整流挡板高度的增加对消除风道出风口纵向分速度、提高风速均匀性都是有利的。

表2 数值模拟计算参数取值表 mm

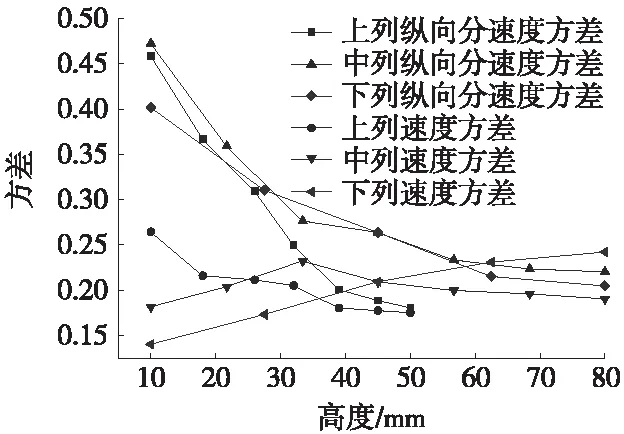
图5 整流挡板对纵向分速度方差、速度方差的影响

3.2 中列整流挡板对出风口射流速度的影响

从图5可以看出，风道出风口处纵向分速度的变化规律类似3.1中所述，随中列整流挡板高度增加而递减；风道出风口风速均匀度随中列整流挡板高度的增加呈现出先降低后增加。故设计中列整流挡板时，在纵向分速度方差满足设计要求的情况下，高度的取值应远离风道出风口风速均匀度最差的点。

3.3 下列整流挡板对出风口射流速度的影响

从图5可以看出，风道出风口处纵向分速度的变化规律同样随下列整流挡板高度增加而递减，但风道出风口风速均匀度同上列风道出风口风速均匀度变化规律相反，表现为随高度的增加而减小，故当纵向分速度方差满足设计要求时，下列整流挡板高度的取值应越小越好。

3.4 正交优化

利用正交试验对上、中、下列整流挡板高度3个参数的4种水平进行优化分析。选择正交表L16(45)进行数值模拟[12]，优化评价指标为风道出风口处的纵向分速度(分速度方差)和风道出风口风速均匀度(速度方差)。对正交仿真结果进行直观分析，得到的直观分析表见表3。

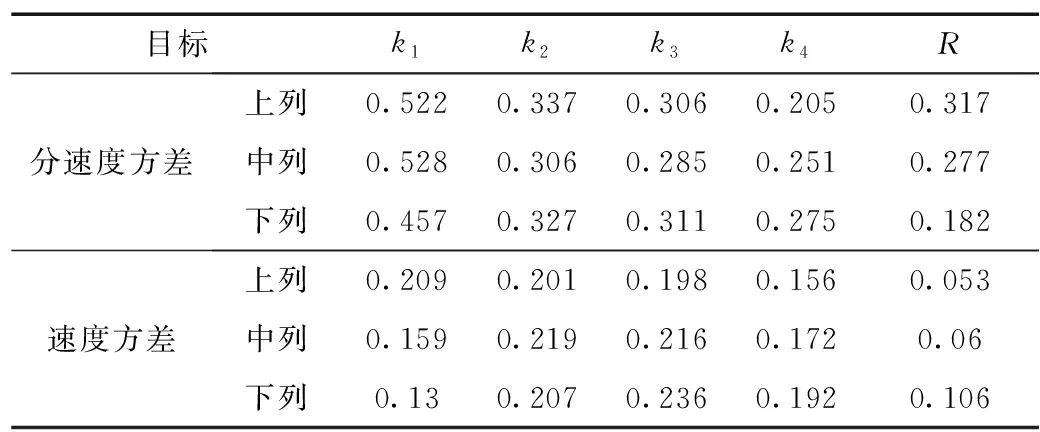
表3 正交结果直观分析表

表3中ki表示正交表中任一列上因素取水平i时所得试验结果的算术平均值，表中R表示极差。

由表3可知，影响风道出风口风速纵向分速度方差的各因素重要顺序为整流挡板上列高度>中列高度>下列高度；影响风道出风口处风速的各因素重要顺序为整流挡板下列高度>中列高度>上列高度。风道出风口处的纵向分速度和速度方差均越小越好，因此由各因素水平对应的k值得到最优设计组合为：风道出风口风速纵向分速度最小的搭配方案为整流挡板上列高度50 mm、中列高度80 mm、下列高度80 mm；风道出风口风速均匀度最优的搭配方案为整流挡板上列高度50 mm、中列高度10 mm、下列高度10 mm。

对正交试验结果进行方差分析，得到的方差分析表见表4。

表4 正交结果方差分析表

由表4可知，上、中、下列整流挡板高度在0.01水平上对消除风道出风口风速的纵向分速度影响显著，下列整流挡板高度在0.01水平上对风道出风口风速均匀性影响显著。因此，要降低风道出风口风速的纵向分速度、提升风速均匀度，在取值范围内要尽量提高下列整流挡板高度，根据实际情况综合考虑调整上、中列整流挡板的高度。