基于多角度线性回归分析的第32届奥运会前十名国家成绩预测
2018-10-20李贵熙綦文彬侯宗润
李贵熙 綦文彬 侯宗润

摘要:本文主要探讨了奥运会奖牌榜的预测问题,主要通过建立线性回归(一元及多元)模型、使用SPSS和Excel等软件对历届奥运会奖牌榜进行多角度分析并得到最优预测模型。在模型一的建立中,本文使用时间序列法进行预测、建立回归模型。由于模型一中对于某些国家奖牌榜预测与实际出入较大,在模型二的建立中,本文综合考虑了GDP,人口数量,东道主效应等因素建立多元回归模型。综合模型一与模型二的求解结果,得到2020年东京奥运会奖牌榜前十名及其金牌数与奖牌数。
关键词:线性回归;时间序列法;奥运会奖牌预测;误差分析;数学建模
中图分类号:O213文献标识码:A文章编号:1672-9129(2018)06-0256-05
Performance Forecast of the Top 10 Countries of the 32nd Olympic Games Based on Multi-Angle Linear Regression Analysis
LI Guixi*, QI Wenbin, HOU Zongrun
(Qingdao Second Middle School, Shandong Province, Qingdao 266000, China)
Abstract:this paper mainly discusses the forecasting problem of Olympic medals list, mainly through the establishment of linear regression(one dollar and multiple elements) model, the use of SPSS and Excel and other software to carry out multi-angle analysis of successive Olympic medals list and get the best prediction model. In the establishment of model one, this paper uses time series method to predict and establish regression model. Due to the large difference between the forecast and the actual number of medals in some countries in model 1, in the establishment of model 2, this paper comprehensively considers the factors such as GDP, population, and host effect to establish a multiple regression model. The results of the comprehensive model 1 and model 2 solutions obtained the top ten medals in the 2020 Tokyo Olympic Games and the number of gold medals and medals.
Keywords:Linear regression; Time series method; Olympic medal forecast; Error analysis; Mathematical modeling
引用:李贵熙, 綦文彬, 侯宗润. 基于多角度线性回归分析的第32届奥运会前十名国家成绩预测[J]. 数码设计, 2018, 7(6): 256-260.
Cite:LI Guixi, QI Wenbin, HOU Zongrun. Performance Forecast of the Top 10 Countries of the 32nd Olympic Games Based on Multi-Angle Linear Regression AnalysisJ]. Peak Data Science, 2018, 7(6): 256-260.
1 引言
1.1 現有研究成果
对于奥运会奖牌预测问题,现在已有如下研究成果:吴殿廷、吴颖[1]使用GM(1,1)模型,预测北京奥运会中、美两国可能会获得的金牌数。Bernard与Busse[2]利用柯布--道格拉斯生产函数对奖牌数分布进行研究。 Condon[3]等人建立人工神经网络模型,预测世界各国在奥运会比赛的成绩积分。
1.2 论文内容、数据介绍及架构
本文根据以往各国奖牌榜排名情况,综合考虑GDP,人口数量,东道主效应等各种能够影响所获奖牌数的因素,建立模型,对2020年东京奥运会奖牌榜前十名国家及其奖牌数与金牌数进行预测,并得到较为成功的结果,对接下来的奥运会训练具有指导意义(见5.2)。
接下来,本文将会介绍模型假设及变量,文章第二部分将使用时间序列法进行一元线性回归模型(模型一)的建立与求解并分析问题与解决方案,第三部分将进行多元线性回归模型(模型二)的建立与求解并分析问题与解决方案,第四部分将对可能影响奥运会金牌数及奖牌数预测的因素举例做出定性(定量内容见4.6)讨论,第五部分将给出各模型及最终预测的结果,第六部分列举本文所用参考文献。
1.3 模型假设
a.假设所有GDP与人口数据准确。
b.假设奥运会当年没有国际争端问题。
c.假设各国GDP与人口与时间呈线性关系。
d.假设不考虑奥运会场地,地理位置,气候等因素的差别。
e.假设每个国家获得奖牌数与往届奥运会获得的奖牌数有关。
f.假设奥运会各项比赛规则、设置不变。
1.4 变量及单位
下表1是本文用到的变量符号及其含义和单位。其余不在本表中列出的变量及单位会在公式后加以说明。
2 模型一的建立与求解
2.1 模型一的建立
关于纵向对比奥运会历史成绩推测与第32届奥运会的影响,本文建立模型一加以说明。模型一通过时间序列法,采用一元线性回归模型,得到奥运会金牌数奖牌数与届数的关系,并通过与后文模型二的对比讨论出两者的优势与不足并进行互补从而得到精确的结果[4]。
时间序列法是一种利用按时间排列的数据预测未来可能结果的方法,在实际应用中范围较广[5]。本文模型一中奖牌数、金牌数与奥运会届数的一元线性回归模型公式如下:
y=α0+α1t+β (1)
其中α1为变量系数,β为常量,α0为随机参数。
下面本文将使用式(1)所用模型进行求解。
2.2 模型一的求解(以韩国为例)
以韩国为例代入一元线性回归模型一中[6]。下表2为韩国第14届至第31届奥运会历史成绩表[7]。
本文利用excel软件进行模型一的建模。下图1为韩国第14届至第31届奥运会金牌数及奖牌数拟合曲线图[8]。
备注:图中x为奥运会届数(t),R2为决定系数,其他见图例
综上所述,韓国金牌数拟合公式如下:
ygold=0.8506t-13.832 (2)
韩国奖牌数拟合公式如下:
ymedal=2.0609t-30.643 (3)
图1中显示(2)(3)式拟合程度R相对较高(85.97%和87.00%,对应R2为0.7391和0.757),该模型通过R检验。代入t=32,可得模型一预测下的韩国第32届奥运会金牌数及奖牌数(13枚,35枚)。
本文接下来用同样方法对其他国家进行一元线性拟合,其中部分方程在经过噪声点处理后拟合程度仍低于50%,其方程仍然列出,但在最后的预测中不会使用经过这些方程计算的结果。详细方程如下表3、表4所示:
2.3 模型一的缺点及可能的改进方案
2.3.1 模型一的缺陷
模型一为一元线性回归模型,变量过少,导致拟合的函数无法满足所需要的结果。其次,在拟合过程中对于奖牌数起伏较大的国家有较大的误差,噪声点明显。
2.3.2 模型一可能存在的改进方案
本文考虑,针对误差较大的问题,可以通过增加变量来解决或者采用局部加权线性回归的方式解决;针对噪声点问题,可以通过去掉不稳定数据后对剩余稳定数据进行分析的结果,或者去掉一个最大值和一个最小值后进行计算的方式来解决该问题[9]。
综合各国奥运会历史成绩,本文根据模型一得出结论:历届奥运会成绩与第32届奥运会预测成绩之间存在一定关系(见表4)。
3 模型二的建立与求解
3.1 模型二的准备工作
一元线性回归模型(模型一)有很多缺陷与不足,而增加变量是减小误差,使数据更加精确的有效办法之一。本文将国家综合实力拆分多个因素(见3.1.1),建立模型二加以讨论。下面文章将建立并求解基于多元线性回归模型进行分析的模型二,同时讨论模型二存在的问题及可能的改进方案。
3.1.1 选用变量
本模型综合考虑国家综合实力和东道主效应对奥运会奖牌数和金牌数预测的影响,选用国家GDP、人口、东道主等变量进行建模。
3.1.2 数据标准化
数据标准化是一种使原始数据转换为无量纲化指标测评值的一种常用方法。因为各国家GDP数值折合当年的美元价格进行计算,所以使用的GDP数据[10]存在量纲不同的情况。本文主要采用min-max标准化(无量纲化),即将原数据映射到[0,1]内,再统一量纲为2016年(第31届奥运会)美元GDP。其公式如下:
(24)
其中X'为标准化之后的数据(单位亿美元),X为原数据(单位为本国货币),X2016为第31届奥运会(2016年)当年该国GDP数据(单位为本国货币)。
3.2 模型二的建立与求解
3.2.1 模型二的建立(以匈牙利为例)
模型二采用多元线性回歸方法进行建模,其公式如下:
y=α0+α1t+α2GDP+α3POP+α4Hold+β (25)
该公式中y为金(奖)牌数,α1、α2、α3、α4均为变量系数,β为常数,α0为随机参数。
下面本文以匈牙利为例建立并求解模型。下表5为匈牙利25届奥运会之后的GDP数据、人口数量[11]、金牌数、奖牌数与东道主变量的统计表:
本文接下来利用SPSS软件,对匈牙利GDP、POP、东道主与金牌数、奖牌数的关系进行分析。详细结果见下表6、7。
以上表6、表7所体现的线性方程均通过了T测验(94.7%和89.9%)和显著性测验(0.021和0.050),证明可以用作模型的解。
综上所述,我们得到了以下两个关于匈牙利金牌数和奖牌数的多元线性回归方程:
ygold=-11.508t-0.003GDP-0.132POP+1669.576 (26)
ymedal=-22.995t-0.004GDP-0.242POP+3114.645 (27)
而在实际计算中,本文将GDP、POP增长速度进行线性回归分析,得到了2020年匈牙利可能的GDP和人口数量(1321.65亿美元,9753.3454万人)。将以上数据带入回归方程(26)(27)中,可以得到2020年匈牙利金牌数和奖牌数的预测值(10金牌,13奖牌)。
3.2.2 模型二的求解
其他国家的模型建立方程基本与匈牙利类似。经检验,其他10个国家(详见1.3)建立的多元线性回归模型中有大部分成立。不成立(未通过测验)的模型依旧在下表8、表9中列出,但是这些模型计算出来的结果不会参与最终预测(详见5.1表11、表12中黑色数据部分)。下表8、表9为其他十国金牌数、奖牌数线性回归分析表。
备注:本表中除德国、匈牙利、俄罗斯等国家GDP、POP、Hold变量因东欧剧变而从第26届奥运会(匈牙利为第25届奥运会)开始采纳分析,日本GDP、POP、Hold变量因东道主分析需要而从第18届奥运会开始采纳分析,中国GDP、POP、Hold变量因中国从第22届奥运会开始参加而从第22届奥运会开始采纳分析以外,其余各国GDP、POP、Hold变量均从第20届奥运会开始采纳分析。下表同此规则。
根据上表8、表9得到的模型二所预测出的结果见表12(见5.1)。
合并GDP、POP、东道主效应等多项因素的影响,本文根据模型二得出结论:国家综合实力影响国家奥运会的成绩,国家实力与该国奥运会成绩基本呈现正相关(见表8、9)。
3.3 模型二的缺陷及其可能改进方案
3.3.1 模型二的缺陷
模型二作为一个多元线性回归模型,其问题集中体现在所建立模型拟合程度较低、容易忽略潜在的交互式或非线性关系、存在多重共线性问题等。
3.3.2 模型二可能存在的改进方案
鉴于3.3.1提出模型二中可能存在的缺陷,本文考虑以下改进方案:忽略噪声点、忽略异常因素(如政治、国际背景等原因)、考虑其他模型(如主成分回归、偏最小二乘回归[12])并进行分析等。
4 对于影响各国在奥运会获得金牌数和奖牌数的其他因素的分析
基于之前的讨论,本文得出结论,国家GDP总量、人口总量、东道主效应对国家获得的奖牌数和金牌数有一定的影响。除此之外,本文经讨论后得出会对金牌数和奖牌数产生一定影响的因素有以下几项:
4.1 国家发展性
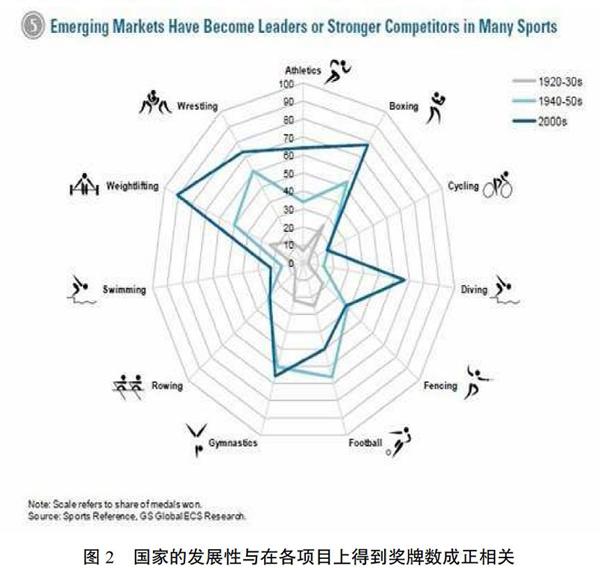
一个统一而强大的国家,更容易在奥运会上会取得优异成绩。以中国为例,1972年前,中国发展缓慢,国家实力弱,无法参加奥运会,没有奖牌,但是随着1972年以后中国政策不断转变,发展性不断增强,近几届奥运会来中国已跻身世界前三,2008年北京奥运会更是在奖牌数上超越美国。可见,国家的综合实力和发展性是影响其奥运会获奖的因素之一(图2)[13]。
4.2 运动员的身体以及心理素质
在奥运会赛场上,选手在身体和心理上的差异会对其发挥产生巨大的影响。如中国运动员刘翔,前后两次奥运会因身体原因而当场弃权。再如,为中国队摘得首金的女射击运动员杜丽,首场比赛失利,她经过场下心理调节后,在接下来比赛过程中发挥出应有水平,最后摘得金牌。
4.3 国家对于体育的支持力度
国家在体育方面的投入和它在奥运会上的成绩呈正相关。对比中美,中国没有在金牌数上超过美国的原因与中国在体育方面的投入不如美国有很大关系[14]。
4.4 举办城市的地理环境
参加奥运会的选手来自五湖四海,各个地区的地理环境有所不同,因此选手们对举办城市的环境的适应也会有所差异,从而影响选手在比赛中的发挥,因而会影响到国家在奥运会上的成绩[15]。
4.5 国家人民对某项运动的热爱(普及)程度
某国家对于某項运动的普及会让更多的人积极参与到该运动之中,有利于该项运动获得更大发展潜力,有利于使该运动在奥运会上取得优异成绩;优异成绩又会提高该国人民对于这项运动的热情与期望,继而拉动整个国家对此运动的投入增加。二者良性循环,互相作用,总体有利于国家成绩的提高。
4.6 国家青少年人口比重
4.6.1 建立模型进行分析
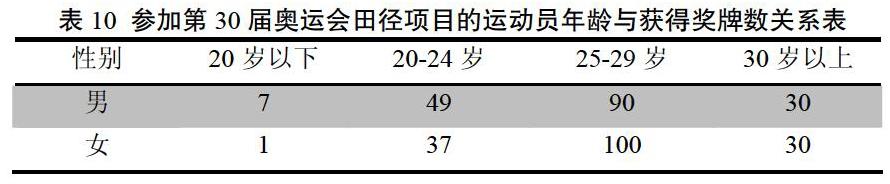
针对本因素,本文将进行定量分析。分析第30届奥运会运动员年龄分布与所获得奖牌数的关系,得到如下表10,参加第30届奥运会田径项目的运动员年龄与获得奖牌数关系表[16]。
4.6.2 对该模型的求解
本文通过SPSS软件对表10数据进行非线性回归分析,发现二次模型对于以上数据较为适合(图3、图4).
其中男、女性年龄与奖牌数的二次关系拟合程度均可到达较高水平(0.97和0.921).本文得出结论,运动员的年龄与其实力的发挥呈二次函数关系。其表达式如下式(48)所示。
ymedal∝age2 (48)
本文列出由SPSS软件拟合的二次方程如下,仅供参考:
![]() (49)
(49)
![]() (50)
(50)
4.6.3 结论
可以看出,年龄相对较小的运动员往往蕴含着更多的可能性和更大的潜力。因此国家青少年占总人口比重是该国取得成绩的重要因素之一。以美国为例[17],美国对青少年体育的投入非常多,这也是中国在奖牌数稍逊于美国的原因之一。
5 第三十二届东京奥运会前十名国家金牌及奖牌数目预测及其意义
5.1 结果预测
综合模型一和模型二以及第四部分的讨论,列出下表11(左)、表12(右)为模型一、模型二所预测的下一届奥运会奖牌数及金牌数前十一名国家。
5.2 意义分析
通过上文的预测可以得出结论,影响国家在奥运会中的获奖情况的因素有很多,对这些因素的分析有利于运动员有针对性的训练和教练的针对性指导,为中国在奥运会上摘金夺银、再创体育佳绩提供参考。
参考文献:
[1] 吴殿廷 ,吴颖. 2008 北京奥运会中国金牌赶超美国的可能性 ——基于东道主效应的分析和预测[J].统计研究 ,2008 ,25 (3):60-64.
[2] Bernard Andrew B , Meghan R Busse.Who Wins the Olympic Games: Economic Resources and Medals Totals [S]. Yale School of Organization and Management, mimeo, working paper ,2000:9-242.
[3] CONDON E M , GOLDEN B L , WASIL E A. Predicting the success of nations at the Summer Olympics using neural networks[J ]. Computer Operations Res 1999 ,26 :1243-1265.
[4] 张玉华,黄河科技学院,河北师范大学学报2013年3月第41卷第2期,基于线性回归动态模型的中国第31届奥运会奖牌数预测
[5] N.T.Thomopoulos著,刘涌康等译:《实用预测方法》,上海科技文献出版社,上海,1980
[6] 中国矿业大学,里约奥运会奖牌榜预测,3-6,http://wenku.baidu.com/link? url=JXipeWt2B6hU-BOHpLqQetLYyHrLJDTgYd3dh0Ol5mB8toDvkluTMzoEEDTBhbAdBKsiLa_xPanYbN6jQ-ojLkj0i0PB43C5DYE57M7hanZ1yKdXG4XQzgfEtXU67eWX
[7] 奥委会官网,http://www.olympics.com/
[8] 郭志军,辽宁对外经贸学员信息技术系,《宁波职业技术学院学报》2009年05期,TP391.13,应用Excel对一元线性回归模型的分析, http://www. cnki.com.cn/Article/CJFDTotal-NZYX200905018.htm
[9] 陳国林,机器学习-回归模型-欠拟合和过拟合,http://blog.csdn.net/ chenguolinblog/article/details/52404765
[10] “汪方操123456”,数据标准化、归一化处理,http://wenku.baidu.com/ link?url=tZ1IuMZWIqzTiGfHHd96exqA6WmWkls9glh10kzW6nYTYKmS8seq4kPnDFl-Krm78awcy76TVF6qIHQJpI-WvzYaFg6T3jYhLM4940EvbDK
[11] 世界银行,http://data.worldbank.org.cn/
[12] 谢小韦、印凡成,河海大学,解决多元线性回归中多重共线性问题的方法分析
[13] 腾讯科技,高盛奥林匹克经济学:用经济模型预测奥运奖牌,http://tech. qq.com/a/20120715/000016.htm
[14] 张亚威,中美体育经济发展比较研究,《智富时代》, 2015(3X)
