水利工程监理委托代理中激励约束与参与约束探究
2018-10-20刘艳平
刘艳平
(辽宁水利土木工程咨询有限公司,辽宁 沈阳 110006)
接受业主的授权和委托并具有专业化、社会化的水利工程建设监理单位即为水利工程建设监理,可对项目的建设按照委托监理合同、工程建设有关法律、法规、国家批准的建设文件以及其他工程建设合同进行监督管理活动[1]。在我国水利工程建筑业的改革和发展中工程监理作为一种有效机制发挥着重要积极作用[2]。考虑到工程监理的委托属性,对于业主与工程监理之间的委托代理关系可利用委托代理理论进行分析,众多学者对其进行了大量研究和探讨[3]。并不是完全竞争的市场经济体制使得我国建筑市场中委托代理模型参与约束(IR)和激励相容约束(IC)不能得到满足的状况经常发生,而是在此条件下的委托代理特征的研究分析相对较少,并且对建筑市场上的一些困惑问题能否采用该特征进行有效处理等问题仍需进一步研究[4]。据此,文章对业主与委托代理之间的关系利用委托-代理模型中的激励约束和参与约束理论进行分析,并对我国水利工程监理管理过程中存在的问题和有效解决方法进行深入探讨。
1 水利工程监理与业主的委托代理模型
水利工程的业主与工程师之间的委托代理模型的基本理论为分布函数的参数优化分析,并作如下基本假设。
(1)工程监理的不确定性工作成果为π,则其工作成果不仅由外界客观条件决定,即与不受业主和工程师控制的外界随机变量相关,而且受其自身努力水平e的作用影响。
(2)业主选择薪酬制度即报酬函数对工程监理进行约束。
(3)自身努力水平为一维连续努力变量,即工程监理的努力水平具有连续性特征[5]。
(4)工程监理的风险特征分别为风险规避和风险中性属性。
结合上述基本假设可对委托代理博弈模型进行分析,并假定工程监理的努力水平e与其参数函数π具有线性相关性,即π=e+θ,并且θ的均值为0、不确定的外生随机因素为正态分布随机变量σ2并等于方差值。所以E(π)=E(e+θ)=e,Var(π)=σ2,其中Var(π)、E(π)分别为π的方差和期望值,并假定利用线性合同即s(π)=α+βπ,其中s(π)为工程监理的总报酬,α、β分别为固定收入和报酬激励强度系数。β为0,1时分别代表工程监理不承担任何风险和承担全部风险。引入v(π-s(π))作为业主的期望效用函数,并且线性合同s(π)=α+βπ具有风险中性基本属性,因此业主的期望收入等于其期望效用,计算公式如下:
E[v(π-s(π))]=E(π-α-βπ)=-a+1-βe
(1)
引入风险规避特征作为工程监理函数的效用函数,因此u=-e-ρw,其中w,ρ分别为实际货币收入和绝对风险规避度量。而努力成本为c(e)=be2/2,其中b为努力成本系数,相同努力时所产生的负效用随b值的增大而增大。因此,考虑到工程监理的风险规避特征其随机收入均值减去风险成本即为确定性等价收入,计算公式如下:
E(w)-ρβ2σ2/2=α+βe-ρβ2σ2/2-be2/2
(2)
式中,E(w)—工程监理的期望收入;ρβ2σ2/2—工程监理的风险成本,β—0则风险成本为0,由于其集成成本可存在正值的状况因此应保留收入水平。
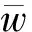
(IR)
结合业主和工程监理的不同特征可将IC划分为信息不对称和信息对称两种情形。
1.1 信息对称分析
业主在信息对称条件下可对工程师的努力水平e进行观测和调整,并在此条件下IC不发挥作用,通过满足IR的监理合同可对任意水平的e进行获取。据此,利用工程监理行为和参数α,β的确定可实现业主期望效用的最大化,并可按照下述公式表征最优化的数学模型:
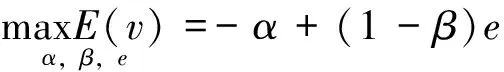
(IR)
上式成立,则在最优条件下可求得最优解,如下所示:
(3)

1.2 信息不对称分析
业主在信息不对称情况下对工程监理的努力水平无法进行观测,据此工程监理的确定性等价收入将按照自身利益最大化原则进行确定,而在此条件下其IC为e=β/b,通过对参数α,β的合理设定业主即可实现自身期望效用的最大化,在此条件下的最优数学模型可表示为:
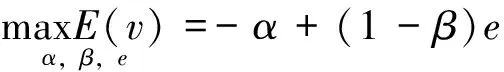
(IR)
e=β/b
(IC)
利用目标函数和IC、IR计算公式,通过一阶求导可得:
β=1+(1+bρσ2)>0
(4)
由上述公式可知β为关于其他参数的递减函数,其值大于0则报酬激励系数为正,此时工程监理需对工程建设承担风险。据此,业主对工程监理的努力水平可观测时,β为0时最优努力水平为e=1/b;若业主对其努力水平不可观测,则β为正时其最优努力水平和风险分担均无法达到实现,并可利用下式表征其最有努力水平:
e=β/b=1/b(1+bρσ2)<1/b
(5)
工程监理在信息对称条件下的努力水平应严格大于信息不对称条件下的努力水平[6],业主对其努力水平不能观测时工程监理为提高自身效用水平可选择e (1)业主和工程监理在信息对称情况下,可按下式进行业主期望收入的计算和求解: (6) 工程监理的确定性等价收入与实际收入相等,公式如下: (7) (2)业主和工程监理在信息不对称情况时,可按下式进行业主期望收入的计算和求解: (8) 在此条件下可按下式进行工程监理的实际收入计算: (9) 通过对比业主期望收入计算公式可知,其期望收益在信息对称条件下大于信息不对称情况;通过对比分析工程监理的实际收入计算公式可知,其期望收益在信息对称情况下小于信息不对称情况。综上所述,作为委托人的业主由于信息的不对称其利益可在一定程度上遭到损害,而作为代理人的工程监理在此条件下可降低努力水平并提高实际收入[7]。 委托代理模型在信息不对称客观情况下可表述为: (IR) e=β/b (IC) 上述模型为理想市场经济条件下的典型委托-代理模型,工程监理按照上述模型可自由决定是否接受工程委托,而在工程监理自身效用最大化和接受报酬方案条件下业主可实现自身效用的最大化。工程监理接受IR为业主选择报酬方案的必要前提条件,并且对工程监理的IR激励也应引起足够的重视[8]。然而目前我国建筑市场的实际经济环境并非如此,在我国实际经济体系中的委托-代理模型和不满足IR、IC条件下的特征仍需要进一步的探讨分析,对工程监理与业主之间的委托-代理模型中的IR和IC研究十分必要。 对于参与约束不成立时,可表述为:对于业主的委托合同工程监理必须接受而无选择的自由。在此条件下业主应考虑工程监理的效用最大化,并且有必要采取措施激励水利工程监理的工作努力程度。业主对水利工程建筑市场也可理解为存在垄断行为,并且考虑到目前建筑市场的特性即处于买方市场特征[9]。 对目标函数引入激励相容约束条件,进而可求得期望收益:E(v)=-α+(1-β)β/b,经过计算求解有:β2=1/2;e2=1/2b;E(v2)=-α+1/4b。工程监理所获取的最优产出相关系数为0.5,并且工程监理的努力成本与业主最大期望收益以及工程监理的最优努力相关。工程监理的努力水平随成本系数的增大而降低,相应的业主期望收益也降低;依据上述结果,若b≥1/4α则业主期望收益可能出现负值或0的状况。 对于激励相容约束不成立的状况可表述为:对于业主的工程建设委托工程监理具有决定权,并且其是否接受合同委托成为业主需要关心的主要问题,而在合同接受后工程监理是否努力工作业主并不特别关注[10]。在不同程度上我国工程监理均可存在上述状况,如监理取费固定制度实施时仅仅是为了应付规章制度和应付检查,委托、代理双方在这种状况下的收益及行为可作如下分析: 利用目标函数并结合参与约束条件转化为-α的等式表达式,其公式如下: (10) 将上述公式进行求导并赋值为0,则可求得: β3=0;e3=1/b (11) 利用目标函数和约束条件可对e3、β3进行求解,结果为: (12) 对于参与约束和激励相容的情形可表述为如下状况:工程监理的积极性不仅得不到激励或尊重,而且对业主的委托合同也无权利是否接受。因此,利用目标函数可对委托代理关系进行求解,结果为:α4=0,β4=0,e4=0,E(v4)=e4。在此状况下,工程监理的努力程度将直接影响业主的收益,然而因为得不到业主的任何奖励工程监理的努力程度往往为0,同时业主的收益也为0,在此条件下不雇佣工程监理即为业主的最好选择。 对于第一类情况,即(IC)和(IR)均可成立,业主重视工程监理的激励机制,并且其选择权可受到尊重,此时产出方差、风险规避度以及成本系数与工程师的努力程度相关。 对于第二类情况,即(IR)不成立而(IC)成立,业主重视工程监理的激励机制,然而工程监理的选择不被尊重。相对于第一种情况工程监理的努力工作程度在第二种情况下更大,并且业主的收益也随努力工作的提升而增大。 对于第三类情况,即(IC)不成立而(IR)成立,业主对工程监理的激励机制并不重视,而对工程监理的选择权利尊重,此时业主的收益为0或为负并且工程监理的努力程度为0。 对于第四类情况,即(CI)和(IR)均不成立,此时业主对工程监理的激励机制不重视并且其选择权不被重视,此时业主和工程监理的努力程度均为0。 在IC不成立以及IR、IC都成立的条件下,双方均有所长,然而在IC、IR均不成立以及IC不成立的条件下其结果均不理想,工程监理的努力水平在业主忽视激励机制时而为0,此时对于业主的收益也会造成一定的损害,据此可判定为该机制为无效机制。 对IR和IC在业主和工程监理的委托-代理模型中进一步分析可知,IC相对于IR更加重要,换句话说为不能满足激励要求的机制即为无效机制。业主可通过必要的成本付出提高工程监理机制运作的有效性,并以此降低工程监理的机会主义行为动机,促进其按照委托合同努力工作,并降低道德风险行为的发生。 通过竞争方式获得工程项目中标为当前我国水利工程建筑市场监理单位的主要方式,监理单位在建筑市场竞争激烈时会考虑其机会成本即保留收入水平为0,监理单位在确定性等价收入大于等于0的条件下均可接受监理委托,即参与约束在目前建筑市场上均可得到满足。然而,为降低投资成本业主对激励措施往往忽视。 某水利建筑工程施工公司分别在2008、2010年进行了两期的某水利工程施工建设,投资金额共8200万元并有甲、乙两家监理公司分别承担项目一期、二期项目。采用固定报酬模式作为一期工程的监理报酬,由于业主对甲监理的监理服务不满意并在2010年更换为另一家相同资质等级的乙监理公司;在二期工程中采用奖励报酬和固定报酬模式作为监理单位的报酬方式,并且按照成本造价、工程质量、是否按照合同要求、按时完工情况等方面作为奖励报酬判别的主要依据。对于两家监理公司的固定报酬由于两期的投资额度相差较大而表现出较大差异,然而其监理效果却相差不大。实践表明,由于对监理单位在二期采用了激励措施,乙监理单位的努力工作程度提升并取得了显著的绩效效益,不仅提升了二期工程而且有利于促进水利工程质量[11]。 而实际上,监理公司的努力水平由于报酬激励的不同而存在一定差异,并最终引起监理绩效的不同。假定甲监理公司和乙监理公司保留收入均为0,其风险规避系数、外生随机变量方差、努力成本系数分别为0.5、0.4;0.6、0.5;0.16、0.16;某水利建筑施工公司未采取激励措施,甲公司在此条件下仅仅有固定报酬并且在报酬上未能体现监理单位是否存在努力工作,因此监理单位在自身利益最大化的原则下会考虑努力的成本支出,此时监理单位会选择不努力工作。业主的收益在监理单位未付出努力时为负,并且对于固定的监理报酬业主白白支付并未实现委托监理的目标。在有激励机制的条件下乙监理的努力水平为正,此时业主可获得一定的最大期望收益。 结果表明,乙监理单位在一定的激励措施下愿意付出更好的努力水平,并最终达到最好的监理效果,从而可实现业主的委托目标。 当前,固定费率为监理单位费用收取的主要方法,即利用建设成本的百分比法对监理费用的进行求解,并且该方法并不有助于促进工程监理的努力工作程度。工程监理可利用信息不对称优势采取机会主义行为或“偷懒”行为并以此提升自身利益的最大化,进而对业主的利益造成损害,最终结果将影响整个工程项目目标。所以,业主有必要对监理单位采取激励措施并以此克服不对称信息所带来的风险,而且在激励措施下工程监理可更加积极、主动地完成委托任务,从而提高业主的整体效益。 完善的制度不仅在制定阶段最优,而且在执行相应时间后也应最优,工程监理制度在经过国家推行和扶持后将进入完全市场化运作,工程监理制度如何推行并继续下去,达到监理单位和业主利益最大化并最终达到“双赢”仍是目前重点关注的问题。1.3 信息不对称下模型的进一步分析
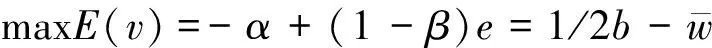

2 激励相容约束与参与约束的拓展研究
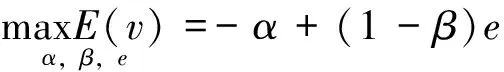
2.1 激励相容与参与约束均成立
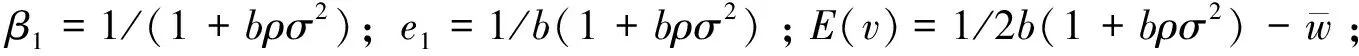
2.2 参与约束不成立
2.3 激励相容约束不成立

2.4 参与约束和激励相容均不成立
3 不同情况分析
4 实例应用
5 结论
