磁悬浮列车转向架的耦合效应研究

邓文熙

（北京磁浮交通发展有限公司长沙分公司，湖南 长沙 410073）

作为21世纪的新型轨道交通，中低速磁悬浮列车有着转弯半径小，爬坡能力强，安静无污染，运行安全系数高等诸多的优点。磁悬浮列车转向架的悬浮控制一般采用四点控制（相互耦合），但通常还是简化为一个电磁铁单点悬浮问题。这种简化有助于我们理解悬浮控制的稳定性和动态特性，便于设计适当的控制律；然而，这提高了控制器的鲁棒性的要求，不适用于工程问题的控制参数整定。在文献[1-4]中，PID控制参数通常根据经验或线性控制理论对单铁悬浮系统的线性化模型进行计算确定；除了电磁力的非线性，还有电流的延迟性，传感器与磁铁的位置偏差等实际约束都没有考虑到，这将影响预期的控制效果。

本文对各文献通常使用的三种物理模型（单铁悬浮线性化模型、单铁悬浮非线性模型、转向架四点控制非线性模型）在相同控制参数下的不同响应进行了对比分析。本文第一节给出了三种模型的带电流环PID控制器的建模过程；第二节以ITAE[5]（时间绝对误差积分）为目标函数对其控制参数进行了优化设计；第三节对阶跃响应进行了比较和分析；最后基于上述分析给出结论。

1 转向架建模

现有文献中出现了很多不同的磁悬浮控制模型，根据不同的需要可能采用不同的物理模型。本文主要建立了业内经常使用的三种模型以便于后续比较：单铁悬浮线性化模型，单铁悬浮非线性模型和转向架四点控制非线性模型。

1.1 单铁悬浮非线性模型

对于单电磁铁悬浮控制系统（图1），当通过电磁体的线圈电流为I，电磁体和轨道的悬浮间隙为时，电磁力Fz为[6]：

式中，N为电磁铁线圈匝数，A为电磁铁极面积，μ0为真空磁导率。

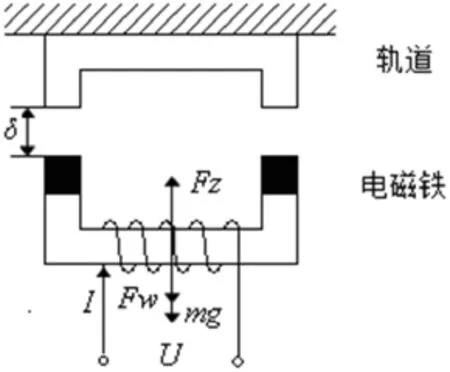
图1 电磁铁单点悬浮控制模型Fig.1 Simple model of the single point magnetic levitation system

电磁铁的动力学方程为：

式中，m电磁铁质量，Fw为电磁铁所示外力或载荷，g为重力加速度。

联合式(1)和式(2)可得到平衡点的间隙δ0下的稳态电流I0：

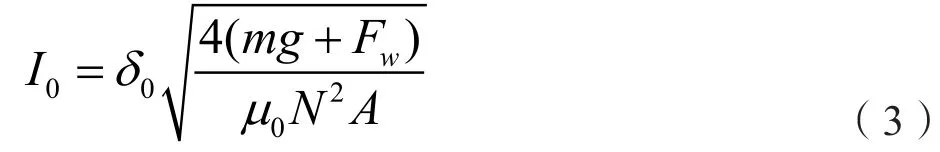
通常，我们采用PID控制，预期电流为[7]：

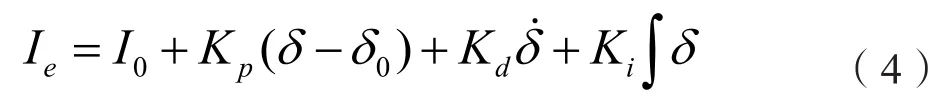
实际工程中，电流控制是通过控制电磁铁两端的电压实现的，通常采用比例控制的电流环来控制的延迟[8]。若电流反馈增益为Kc，则该控制器输出电压为：

若电磁铁线圈电阻为R，根据电压方程可知[8]:

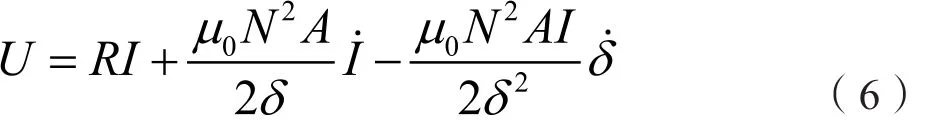
1.2 单铁悬浮线性化模型

根据方程(1)和(2)，电磁力可线性化为：

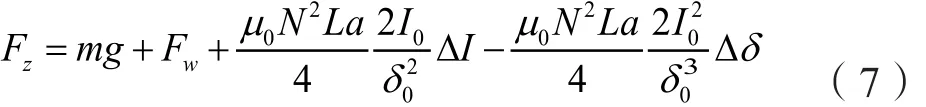
根据方程(4)，控制电压可线性化为：

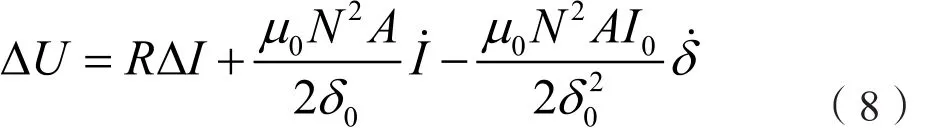
1.3 转向架四点控制非线性模型

转向架是磁悬浮列车的基本单元，可提供悬浮力和推力，它主要由两个悬浮模块和两套防滚解耦机构组成[9]，其力学模型如图2所示。

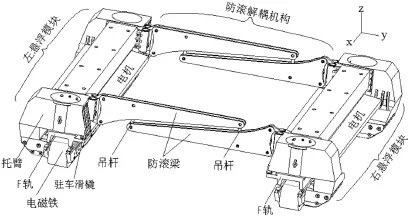
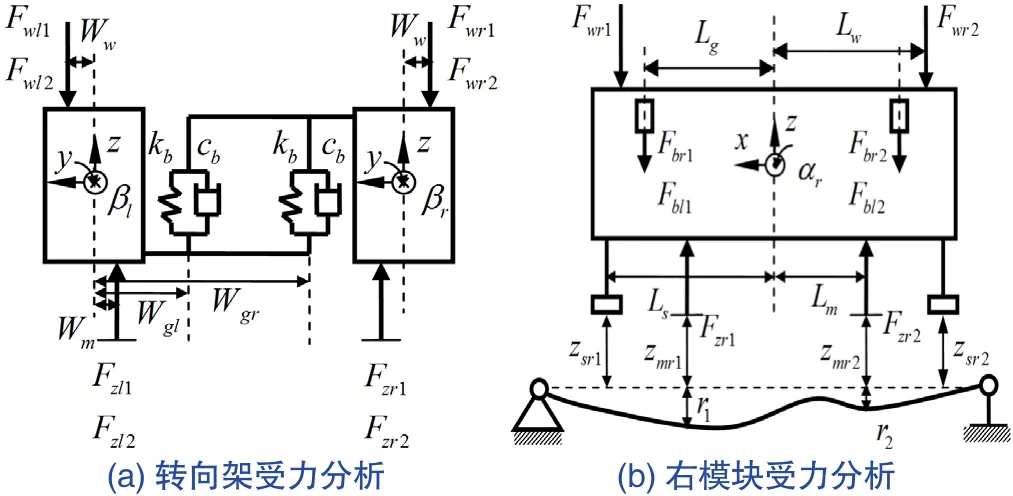
图2 单转向架的物理模型Fig.2 Sketch of the maglev bogie on track

以右模块为例，包括模块重力mrg，前、后托臂受到空簧传递过来的负载力Fwr1、Fwr2，电磁铁的悬浮力Fzr1、Fzr2。此外，左、右模块之间由防滚梁和吊杆连接，模块还受到吊杆力Fbij。模块的前、后位置分别以下标1、2表示，左、右分别以下标l、r表示。电磁力和吊杆力[10]分别满足下式：

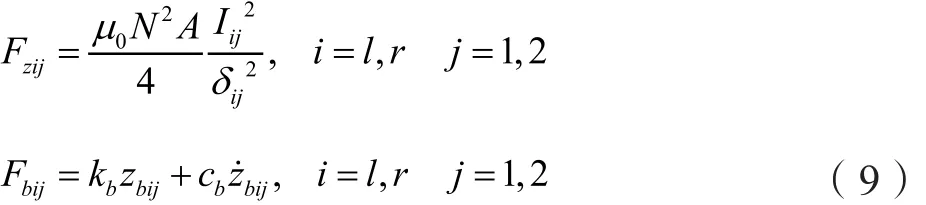
式中，zbij为吊杆变形量，kb、cb分别为防滚吊杆的刚度和阻尼。其中δij、zbij可由悬浮架的几何关系以及两模块的位姿参数解出。

对于单个悬浮架，仅考虑单悬浮架的沉浮运动、俯仰运动和侧滚运动，其动力学方程[10]为：

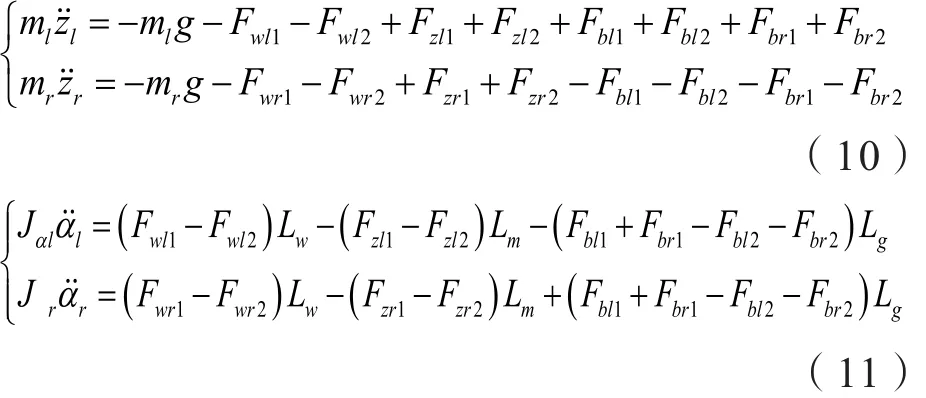
表1 建模参数Table 1 Modeling parameters

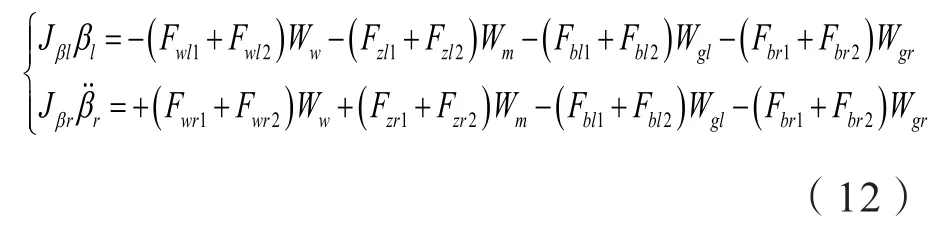
式中，z、α、β分别为模块的z向位移、俯仰角和滚动角，mi、Jαi、Jβi分别为模块的质量、俯仰惯量和滚动惯量，Lm、Lw、Lg分别为控制力、负载力、左右吊杆力作用点距离模块质心的x向距离，Wm、Ww、Wgl、Wgr分别为控制力、负载力、左右吊杆力作用点距离模块质心的y向距离。

2 优化模型

通常，控制参数的整定是通过遗传算法等优化算法优化控制参数（Kp，Ki，Kd，Kc）使得阶跃响应（1 mm）下的性能指标ITAE最小，目前一般采用第1节所描述的单点控制模型作为优化对象。为了避免仿真发散影响评估，我们通常会限制这些参数的搜索范围。优化问题可描述为：

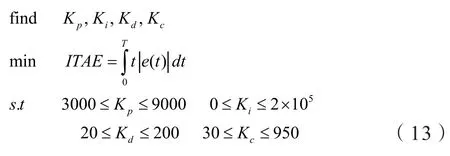
本文在Matlab中建立了第一节所描述的三个模型，均采用表1所列出的参数，优化算法均采用采用多岛遗传算法。对于单铁悬浮线性化模型的优化结果为：Kp=4972，Ki=0，Kd=54，Kc=33。对于单铁悬浮非线性模型，优化结果为：Kp=4929，Ki=0，Kd=54，Kc=79。

3 仿真分析

图3比较了在悬浮间隙由9 mm变化为10 mm情况下，单铁悬浮线性化/非线性模型的响应和ITAE指标。控制参数由单铁悬浮线性化模型的ITAE优化结果确定。根据该优化结果，PID控制器是PD控制器，因为Ki=0。结果表明，相对于线性化模型，非线性模型的电磁铁控制效果不佳，并导致了更大的ITAE，调节时间较长，超调量也较大。这意味着基于线性化模型整定的控制参数在实际中的单点悬浮工况也不能很好地工作。

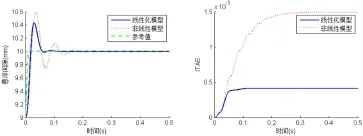
图3 单铁悬浮线性化模型优化控制参数下的阶跃响应及其ITAE指标（Kp=4972，Ki=0，Kd=54，Kc=33）Fig.3 Step responses and performance of single point magnetic levitation (Kp=4972, Ki=0, Kd=54, Kc=32)

图4比较了在单铁悬浮非线性模型优化的控制参数下，单铁悬浮线性化/非线性模型的响应和ITAE指标。结果表明，这两种模式的收敛速度都很快。相比而言，非线性模型的ITAE降低了得多，而线性化模型的ITAE增加不大。控制参数的显著变化是Kc从32变为79，这表明电流环在悬浮控制中非常重要。

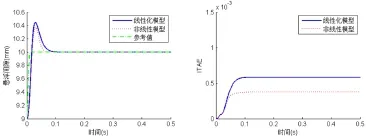
图4 单铁悬浮非线性模型优化控制参数下的阶跃响应及其ITAE指标(Kp=4929, Ki=0, Kd=54, Kc=79)Fig.4 Step responses and performance of single point magnetic levitation (Kp=4929, Ki=0, Kd=54, Kc=79)

图5 单铁悬浮非线性模型优化控制参数下转向架的阶跃响应(Kp=4929, Ki=0, Kd=54, Kc=79)Fig.5 Step responses of bogie maglev model (KP=4929, Ki=0, Kd=54, Kc=79)

图5给出了单铁悬浮非线性模型优化控制参数下转向架的阶跃响应（1 mm阶跃干扰仅作用在左前点）。结果表明，四个点的收敛时间均小于0.1 s，但均存在静差。在左侧前后点的耦合效应比其它两个点更显著因为它是相同的刚性模块上。这表明基于单点悬浮模型整定的控制参数仍不适用于磁悬浮列车。

磁悬浮转向架的耦合效应取决于前后防滚解耦机构间距、防滚吊杆的刚度等机械参数；图5还给出了2倍防滚刚度下的转向架阶跃响应。结果表明，静差随刚度kb的增加而增加，这意味着耦合效应被增强。为了保证直线感应电机的离轨间隙，防滚吊杆刚度必须足够刚，设计时须对其防滚和解耦性能进行权衡。

4 结论

本文建立了磁悬浮列车单转向架四点控制模型，考虑了转向架垂直，俯仰和滚动方向的自由度及其耦合关系；与电磁铁单点控制线性化/非线性模型的闭环阶跃响应进行了比较。仿真结果表明，基于单铁控制线性化模型和非线性模型得到的最佳控制参数一样不适合转向架模型，主要因为转向架的耦合效应导致其控制存在静态误差；这种耦合效应与前后防滚解耦机构间距、防滚吊杆的刚度等机械参数有关。因此，转向架四点控制模型应作为基本单元进行响应分析进而对整车悬浮控制参数进行整定。