油罐运输车有限元分析及优化
2018-10-20焦学健苏尚彬丁后颂
邢 帅,焦学健,苏尚彬,丁后颂
(1.山东理工大学 交通与车辆工程学院,山东 淄博 255049;2.山东工业职业学院 冶金与汽车工程系,山东 淄博256414;3.威海职业学院 交通工程系,山东 威海 264200)
油罐运输车有限元分析及优化
邢 帅1,焦学健1,苏尚彬2,丁后颂3
(1.山东理工大学 交通与车辆工程学院,山东 淄博 255049;2.山东工业职业学院 冶金与汽车工程系,山东 淄博256414;3.威海职业学院 交通工程系,山东 威海 264200)
为验证油罐运输车的结构强度是否满足使用要求,运用有限元仿真分析方法分别建立其弯曲、扭转、紧急制动3种工况的模型并进行了最大应力分析.结果显示,罐体结构的应力小于材料的屈服应力,在满足使用要求的基础上,采用尺寸优化分析方法减薄罐体的厚度可实现轻量化.
油罐运输车;有限元分析;尺寸优化
伴随着世界经济持续发展,石油、天然气的需求逐步增加,油罐车作为短途运输交通工具发挥着重要的作用.存在部分结构不合理和整车质量过重现象及潜在运输的危险性,同时使得运输成本增加.因此基于CAD/CAE技术对整车进行结构分析与轻量化设计[1],可以提高产品的科技含量,为企业以后的生产提供设计指导.
1 罐车有限元模型的建立
1.1 单元类型的选择
罐体单元主要采用单元类型中的壳单元来划分网格,车架部分由于用梁单元不能分析应力集中问题,所以同样采用壳单元来划分车架网格,这样可以准确地得出分析结果.罐体的单元选用四边形壳单元(QUA D4),在几何形状复杂的位置可以采用少量的三角形单元(TRIA3)来过渡,以满足总体网格质量的要求,通常要求三角形单元占总单元数的比例不超过5%[2].罐体以及车架的单元全部为10mm尺寸单元.
1.2 罐体与车架连接方式
罐体与前后封头、罐体与防波板以及加强板与相应连接部件之间用节点耦合的方式模拟焊接.利用RBE2单元将孔周围的单元连接来模拟边支梁、车架之间的螺栓连接,能够比较真实地反映构件之间力的传递,如图1所示.大梁与副车架之间的连接采用ACM单元.ACM单元模拟的是一种特殊的焊接方法(Area Contact Method),不同于刚性单元结点连接的方法.它是由一个六面体(SOLID)和RBE3(1D)单元组成,更能准确模拟焊点信息,不会增加局部的刚度[3],如图2所示.

图1 边支梁和车架连接方式Fig.1 The connection of the beam and the frame

图2 大梁与副车架连接关系Fig.2 The connection of beams and the auxiliary frame
1.3 钢板弹簧有限元模型
由于半挂车的悬架采用钢板弹簧,为了使模型接近实际情况,采用单片钢板弹簧代替多片钢板弹簧.单片板簧采用壳(QUAD4)单元进行划分,卷耳销轴采用1D梁(BEAM)单元代替,将板簧的上边缘节点与卷耳销轴的对应节点通过多点约束(Multiple Point Constrain)的方式进行耦合,使得板簧与吊耳之间只能发生沿卷耳轴线的相对转动.油罐整车模型的约束施加在钢板弹簧的中间部位,约束x、y、z3个方向的平动自由度.
在有限元模型中,采用具有一定厚度的壳单元(QUAD4)模拟钢板弹簧的刚度,通过壳单元厚度的改变实现钢板弹簧刚度的变化.钢板弹簧模型如图3所示.板簧A端约束x、y、z3个方向平动自由度,B端约束y、z2个方向的平动自由度,放开沿车架纵向(x方向)的自由度.在C位置施加一排均布载荷,根据公式[4]
δ=F/K
(1)
计算出钢板弹簧的刚度,δ为C点挠度.通过调整单元的厚度改变δ,当单元厚度为36mm时,K=1 420N/mm.
对罐车各个部分结构划分网格后,通过不同的连接方式将各部分连接,建立整车有限元模型如图4所示.

图3 钢板弹簧有限元模型Fig.3 The model of leaf spring

图4 罐车有限元模型Fig.4 The tanker vehicle model
2 罐车静力分析
2.1 液体载荷施加
汽油与罐体表面接触,各处压强与该处液面深度有关,假设汽油的密度是均匀的,其值为0.76×10-9t/mm3,则汽油对罐体的作用力可通过压强公式来计算.
p=ρgh
(2)
式中:p为汽油在罐体某一位置的压强(MPa);ρ为汽油的密度,取值为0.76×10-9t/mm3;h为罐体某一点处的高度(mm);g为重力加速度,取值为9 800mm/s2.
2.2 匀速行驶工况
(1)载荷施加:载荷由结构自重2.9t和汽油的重量35t组成.
(2)约束条件:在全局坐标系下,对牵引板施加x、y、z方向的平动自由度,同时约束钢板弹簧与车轴连接6个位置x、y、z方向的平动自由度.
(3)结果分析:如图5所示,罐体在承受结构自重以及液体压力的情况下,大部分区域应力较小,后封头与罐体连接位置的应力约在18~80MPa.罐体本身、后封头以及车架焊接处应力较大,最大应力为90MPa.如图6所示,防波板与车架连接的部位应力在20~40MPa,其中第一块防波板与车架连接位置的应力较大,最大应力为116MPa.如图7所示,车架与吊耳的连接部位应力在30~190MPa.最大应力出现在车架与前部第一对吊耳连接位置,其值为194MPa.
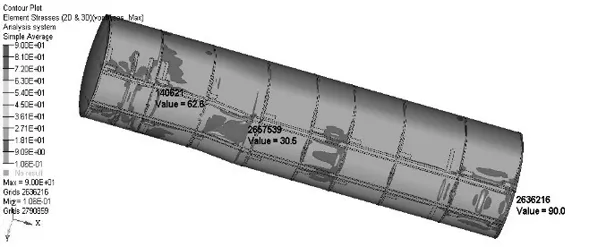
图5 匀速行驶工况罐体应力云图Fig.5 The stress of the tank under constant speed driving condition
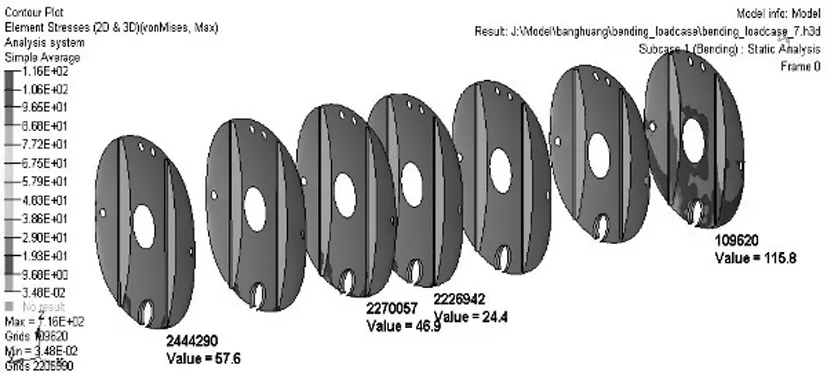
图6 匀速行驶工况防波板与加强筋应力云图Fig.6 The anti-wave board and stiffener stress under constant speed driving condition

图7 匀速行驶工况车架应力云图Fig.7 The stress of the tank frame under constant speed driving condition
2.3 扭转工况
(1)载荷施加:由结构自重2.9t和汽油重量35t组成.
(2)约束施加:在全局坐标系下,对牵引销板施加x、y、z方向的平动约束,释放右后侧钢板弹簧与车轴连接位置的约束,其余位置约束x、y、z方向的平动.
(3)结果分析:由图8可知,罐体大部分应力小于12MPa.应力较大的位置出现在罐体前后部与车架连接的部位,最大值为141MP.由图9所示扭转工况可知,防波板与车架及加强筋底部的连接部位的应力约在10~80MPa,最大应力110MPa,发生在第一块防波板与车架连接的位置.由图10可知,牵引板位置处的横梁的应力值约在20~90MPa.最大应力为282MPa,出现在最后吊耳与车架的连接位置.
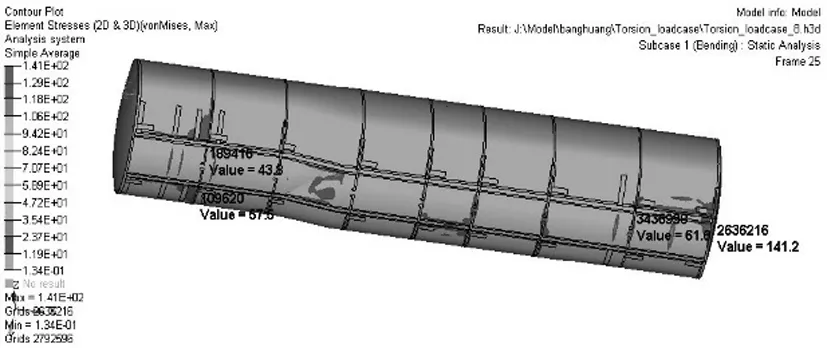
图8 扭转工况罐体应力云图Fig.8 The stress of the tank under torsional working condition
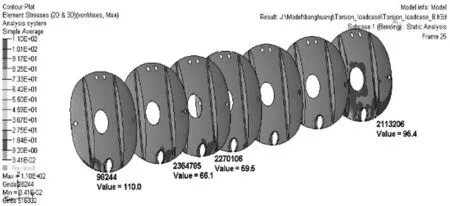
图9 扭转工况防波板及加强筋的应力云图Fig.9 The anti-wave board and stiffener stress under working condition of torsional

图10 扭转工况车架应力云图Fig.10 The frame stress under torsion condition
2.4 紧急制动工况
(1)载荷施加:在紧急制动时,取制动加速度ax=7 000mm/s2.载荷由结构自重2.9t,汽油的重量35t以及制动惯性力组成.制动惯性力由结构惯性力和汽油惯性力组成.
结构惯性力:在全局坐标系下,施加一个沿x轴负向的惯性载荷.
汽油惯性力:F=max.式中:m为罐体各个部分储存汽油的重量;ax为制动加速度,以压力的方式施加在罐体前部封头以及各个防波板上.
(2)约束施加:在全局坐标系下,对牵引销板施加x、y、z方向的平动变形约束,同时约束钢板弹簧与车轴连接6个位置x、y、z方向的平动自由度.
(3)结果分析:由图11可知,罐体前半部分以及罐体与前封头连接部位的应力在20~50MPa.应力最大值为53MPa,出现在罐体、车架及第一块防波板的连接位置.如图12所示,防波板以及罐体加强筋的大部分区域的应力小于9MPa,每一块防波板与罐体的连接位置出现应力相对较大的区域,应力约在8~60MPa.最大应力出现在第一块防波板与车架的连接位置,最大应力为99MPa.如图13所示,应力相对较大的位置出现在车架与第一对吊耳的连接位置,牵引板位置的应力约在20~83MPa.车架与第一对吊耳连接位置处的应力为130MPa,没有超过材料的许用应力.
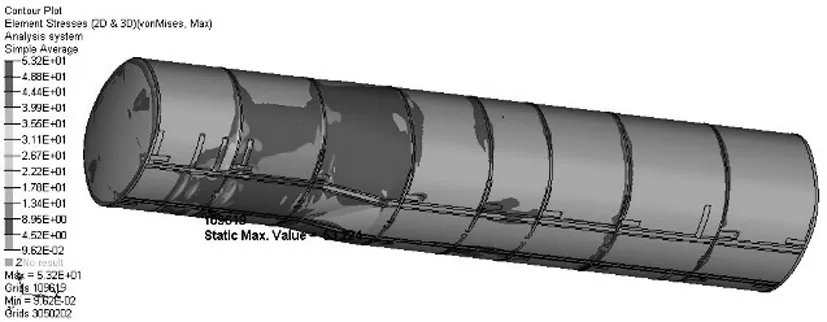
图11 紧急制动工况罐体应力云图Fig.11 The tank stress under the braking condition

图12 防波板与加强筋应力云图Fig.12 The anti-wave plate and the reinforced stress
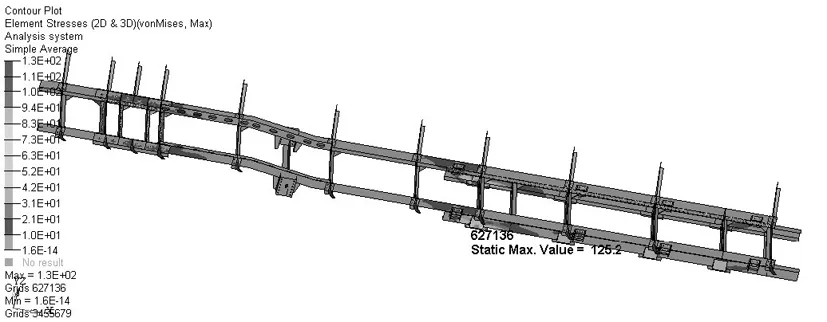
图13 紧急制动工况车架应力云图Fig.13 The stress of the frame under the braking condition
通过对油罐车3种工况的静力分析及仿真结果可以看出,罐体以及防波板大部分位置的应力值都比较低,远小于材料的屈服强度.
3 尺寸优化
3.1 尺寸优化理论
以油罐车罐体及防波板尺寸优化设计为例,设油罐车罐体及防波板的壁厚为xi(i=1,2,…,n,n为罐体及防波板的总数),罐体及防波板的体积为V(X),约束条件为应力,则车架的尺寸优化设计数学模型可表示为[5]
求:X={X1,X2,…,Xn}T
使: minV={V0,V1,…,Vn}
满足:Xi min Sj≤{S10,S20,S30,…},j=1,2,…,m 式中:X={X1,X2,…,Xn}T为尺寸优化的设计变量;V0为尺寸优化计算的体积;Xi min和Xi max分别为第i个构件厚度的约束下线和上限;Sj为第j个单元的计算应力值;Sj0为第j个单元的许用应力值;m为罐体及防波板有限元计算模型网格单元的总数. 结构的尺寸优化就是在结构拓扑确定的前提下,建立针对尺寸参数合适的数学模型,再使用优化方法来求解该模型并最终得到优化后的尺寸参数.另外,在尺寸优化设计的过程中,为了不使边界形状和结构的拓扑形态发生改变,只能调整一些特别规定的尺寸[6].最终优化尺寸见表1. 表1 罐体及防波板最终优化尺寸 部件尺寸下限/mm尺寸上限/mm最终尺寸/mm罐体前封头3.54.04.0防波板13.03.53.5防波板22.53.03.0防波板32.02.52.5防波板44.55.04.5防波板54.55.04.5防波板64.55.04.5防波板74.55.04.5罐体后封头6.06.56.0罐体4.04.54.5 (1)设计变量:将板材厚度作为设计变量,设置优化区间. (2)约束条件:结构应力小于静力分析过程中罐体承受的最大应力(140MPa). (3)目标函数:体积最小化. 根据优化结果建立罐车3种工况下的验证模型,经过仿真分析得出优化后的罐体、防波板及车架的应力结果,优化前后罐体及防波板的应力对比见表2. 通过对比分析优化前后罐体的应力可知,优化后的最大应力没有超过材料的屈服强度,满足罐车的使用要求,证明了优化方案的可行性. 表2 验证模型对比分析 工况及优化前后应力罐体及防波板车架及加强件匀速行驶工况优化前优化后最大应力/MPa90192最大应力位置第一块防波板与罐体及车架的连接位置左侧第三个吊耳与车架的连接位置最大应力/MPa95190最大应力位置第一块防波板与罐体及车架的连接位置第一块防波板与罐体连接位置的三角形加强板处扭转工况优化前优化后最大应力/MPa156282最大应力位置最后一块防波板与车架及罐体的连接位置右侧第二个吊耳与车架的连接位置最大应力/MPa167320最大应力位置最后一块防波板与车架及罐体的连接位置右侧第二个吊耳与车架的连接位置紧急制动行驶工况优化前优化后最大应力/MPa99125最大应力位置第一块防波板与罐体及车架的连接位置两侧第一个吊耳与车架的连接位置最大应力/MPa120127最大应力位置第六块防波板与车架及罐体的连接位置两侧第一个吊耳与车架的连接位置 通过对罐车道路行驶中的3种工况进行有限元分析可知,罐车整体及局部的应力均未超过材料的屈服应力,满足其使用要求.同时,在此基础上对罐体及防波板运用尺寸优化的方法,优化出板厚的最佳尺寸以达到减轻整车重量的目标.最后,建立了优化后的验证模型,分析结果显示优化后的应力同样满足要求. [1]彭超.以轻量化为目标的某乘用车车身优化设计与研究[D].邯郸:河北工程大学,2015. [2]胡西. 散装水泥车罐体有限元分析与改进[D]. 长沙:湖南大学, 2012. [3]许冰, 胡强, 涂小春,等. 白车身焊点缩减拓扑优化对车身性能研究[J]. 企业科技与发展, 2013(13):84-86. [4]柴山, 郭明, 徐上海,等. 车辆钢板弹簧悬架的有限元模型[J]. 江苏大学学报(自然科学版), 2015, 36(1):16-22. [5]成耀龙, 马力, 王皎. 重型专用车车架轻量化结构优化设计[J]. 专用汽车, 2006(2):29-32. [6]朱帅. 半挂油罐车结构有限元分析及半挂车车架优化设计[D]. 合肥:合肥工业大学, 2007. Finiteelementanalysisandoptimizationofoiltankcarrier XING Shuai1, JIAO Xue-jian1,SU Shang-bin2,DING Hou-song3 (1. School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China;2. Metallurgy and Automotive Engineering Department, Shandong Vocational College of Industry, Zibo 256414, China;3. Transportation Engineering Department, Weihai Vocational College, Weihai 264200, China) In order to test whether the structure strength meets the requirement of the vehicle tank, the finite element model for three kinds of working conditions including bending,torsion and emergency braking was established using finite element simulation analysis method, and analyzed it′s the maximum stress. Most of the structure of tanks and frames stress is less than that of the material, and on the basis of satisfing the using requirements,we use the method of size optimization to reduce the thickness of the tank and achieve lightweight. oil tanker; finite element analysis; size optimization 2016-11-18 邢帅,男,707254336@qq.com; 焦学健,男,jeosword@126.com 1672-6197(2018)01-0039-05 U463.82 A (编辑:郝秀清)3.2 罐体及防波板的尺寸优化
Tab.1 The final optimum size of the tank and anti-wave plate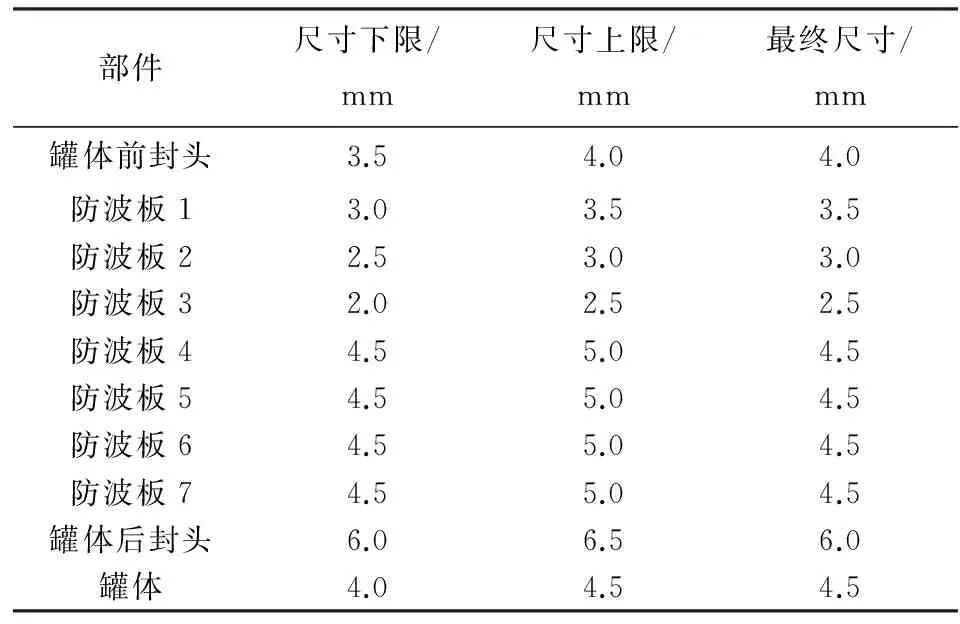
3.3 优化前后模型对比分析
Tab.2 The contrast analysis of validate model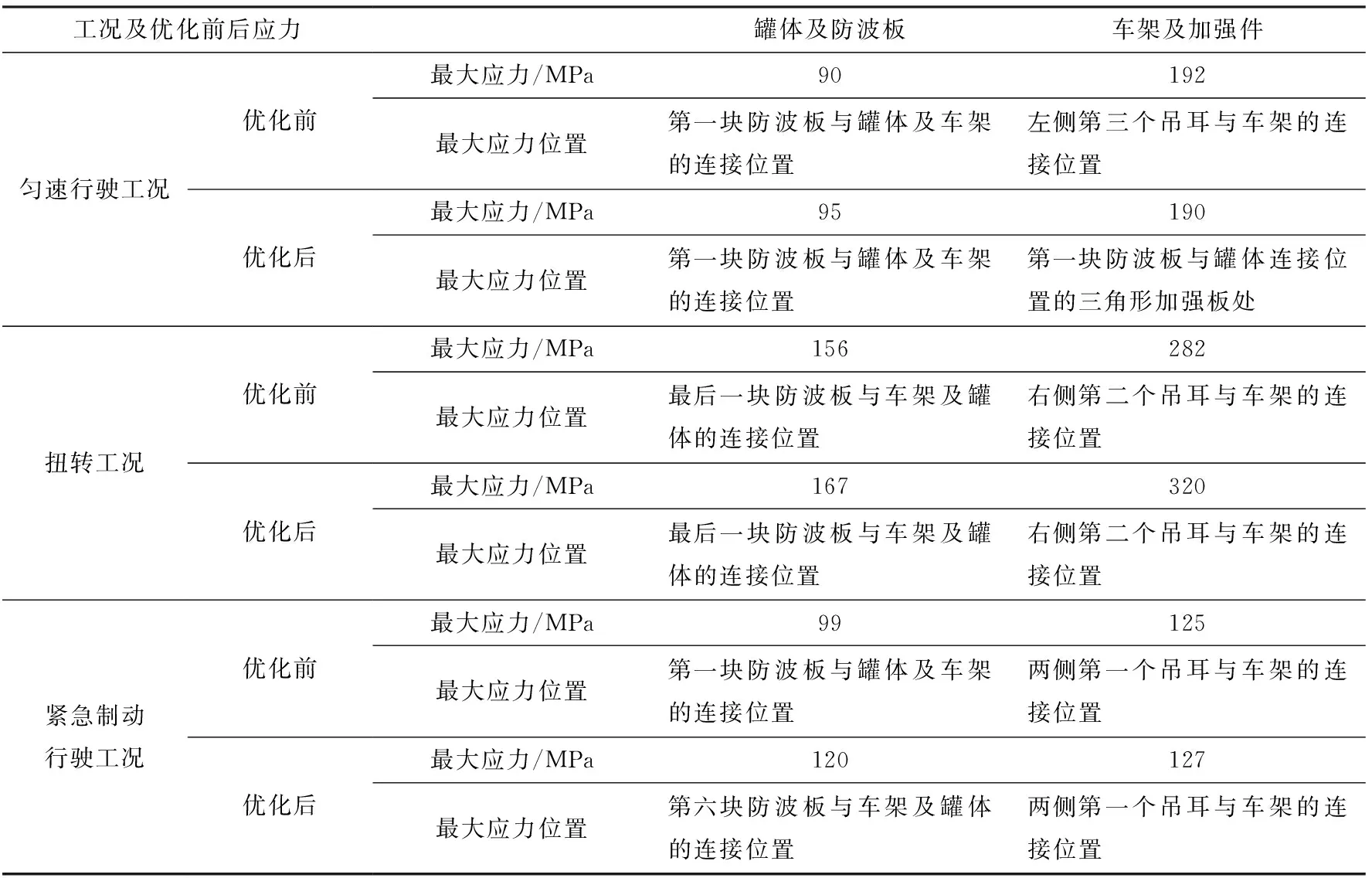
4 结束语
