高速铁路无砟轨道绝对测量模式分析与复合测量模式探讨

2018-10-20吴维军朱洪涛孟繁国王东益曹娟华

铁道标准设计 2018年11期

吴维军,朱洪涛,孟繁国,孙启,王东益,曹娟华,5

(1.南昌大学机电工程学院,南昌 330031； 2.中国铁路沈阳局集团有限公司通辽工务段,辽宁通辽 028001； 3.中国铁路哈尔滨局集团有限公司哈尔滨工务段,哈尔滨 150000； 4.沈阳铁路局集团有限公司山海关工务段,河北秦皇岛 066200； 5.江西制造职业技术学院,南昌 330095)

为实现列车高速行驶的安全、稳定和舒适，保证轨道的高稳定性和高可靠性，需要对轨道进行精确测量和精细调整[1]。在高速铁路轨道建设阶段，线路精调测量主要采用以CPIII控制网为基准的绝对测量模式，该测量模式以客运专线轨道测量仪为代表[2]。绝对测量模式以《高速铁路设计规范》[3]或《高速铁路无砟轨道工程施工精调作业指南》[4]中的精调作业验收标准为依据，对逐枕的轨道绝对位置偏差(横向偏差和高程偏差)和平顺性偏差(10 m弦短波、30 m弦5 m校核中波及300 m弦150 m校核长波等的轨向偏差和高低偏差，根据轨道前后相对位置偏差计算得到[5-6])计算轨道调整量，指导轨道精调。

在高速铁路建设和运营维护中，由于控制轨道绝对位置和线路线形的需要，以及列车运行速度提升后控制线路长波平顺性的需要[7]，才使以坐标测量和绝对位置控制为核心的绝对测量模式成为轨道精调测量的主要手段和方法。但全站仪需要置平才能设站和数据需要逐枕采集的测量方式，决定了绝对测量的测量效率(0.2～0.3 km/h)无法再度提高。同时，作为绝对测量核心器件的全站仪，是集测距测角于一体的高精密电子测量产品，为保证其测量的高精度，内部嵌套了水平补偿、温度补偿、大气改正等测量补偿算法，对使用环境条件要求颇高，日照、下雨、风大或湿气大等环境不适合测量作业[8]。因此，绝对测量效率低、环境适应性差，尤其是在高速铁路运营线路天窗时间短的情况下，难以满足使用的要求。

同时，在轨道精调中，TQI轨道质量指数常被用于轨道精调效果的评价[9]，而精调后TQI扣分最多的往往又是轨向和高低的中短波平顺性，既有的绝对测量技术对于保证高速铁路±1 mm的短波平顺性比较困难[10]。而以轨道检查仪为代表的相对测量技术，以高精度的光纤陀螺仪为主要元器件，以惯性非接触测量为主要方式，具有连续测量效率高和中短波平顺性精度高的优点，主要应用于运营线路的日常检查和养护维修。因此，以绝对测量模式为基础，结合相对测量模式，探讨是否存在更为合理、高效的测量模式和数据处理方法，具有工程价值和现实意义。

1 轨道中线坐标计算与误差表示

绝对测量模式以CPⅢ控制网为基准，通过自由设站、小车棱镜坐标测量及轨道中线坐标计算，得到逐枕的轨道空间三维坐标，包括轨道中线三维坐标和左右轨三维坐标，结合设计线形计算得到水平方向的横向偏差和铅垂线方向的高程偏差，用以实现轨道绝对位置的控制[11]。绝对测量系统主要由测量小车、全站仪和通讯模块等组成，三角架在轨道道床上架设，对全站仪进行人工整平(使全站仪坐标系xoy平面与工程独立坐标系XOY平面处于平行状态)，测量6～8个CPⅢ控制点后完成后方交会自由设站[12]。设站后，全站仪跟踪并测量小车棱镜，得到小车棱镜点的测距测角信息(测量距离l，水平角α，天顶距角β)。结合设站信息中的站点坐标(x0，x0，z0)和设站方向角θ，得到工程独立坐标系下小车棱镜的空间坐标(xp，yp，zp)[13]

(1)

由于全站仪测量小车棱镜时，通常采用半测回测量，存在一定的i角误差[14]，因此，对公式(1)中小车棱镜的高程坐标进行了修正，i为全站仪半测回测量时的i角误差。

以小车棱镜点为小车的特征点，结合已知的小车结构参数和姿态测量成果计算轨道中线的三维坐标。首先，以小车棱镜点坐标(xp，yp，zp)为原点，建立小车空间直角坐标系O′-X′Y′Z′：以轨道所在方向为X′轴，里程增大方向为正方向；以轨检仪横梁方向为Y′轴，与X′轴正交；Z′轴与X′轴和Y′轴正交，方向向上为正，三坐标轴位置关系符合左手定则，如图1所示。

图1 轨道中线三维坐标转换

(2)

式中T——小车棱镜中心到小车左侧臂的水平距离；

H——小车棱镜到轨道面的垂直高度；

g——轨距测量值。

其次，根据空间坐标变换原理[15]，建立测量小车空间直角坐标系与工程独立坐标系之间的坐标转换关系，得到轨道中线的三维坐标

(3)

γ为轨道面与水平面在轨道纵断面上的夹角，由小车内倾角传感器测量得到，φ为线路方向角，因此，轨道中线坐标可表示为

(4)

由公式(4)可知，轨道中线坐标是关于多个变量的函数，根据泰勒展开，将其表示为微分形式，得到轨道中线坐标的误差表示方程

(5)

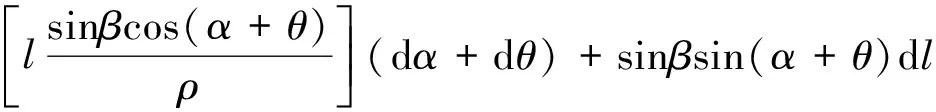
(6)

(7)

其中：ρ=206 265〃

2 绝对测量精度分析(图2)

虽然测量的是轨道中线坐标，但指导轨道精调的是横向偏差和高程偏差。如图2所示，线路中线横向偏差的误差分量ds，可由轨道实际中线坐标的误差分量dx和dy计算得到

ds=sinφdx-cosφdy

(8)

图2 轨道中线测量误差分解

将公式(5)、公式(6)代入公式(8)，dl的系数项为sinβcos(α+θ)sinφ-sinβsin(α+θ)cosφ。当全站仪在轨道中线附近架设时，线路方向φ≈α+θ，即测距误差在线路横向的误差分量很小或约等于0。所以，在实际测量中，应尽量将全站仪架设于轨道中线位置，使测距误差的分量最小。将公式(7)、公式(8)进行整理，表示为矩阵形式

dY=FdX

(9)

其中，

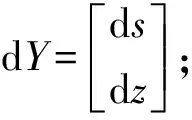
dX=

F为2行10列的系数矩阵，是轨道中线坐标对各变量的偏导数。由此可知，轨道中线横垂向偏差测量误差主要来源于3方面：(1)轨距误差、水平误差等小车内部传感器的测量误差；(2)全站仪设站误差；(3)与直接观测值l、α和β有关的站内各点的相对点位误差。

根据协方差传播定律可得

(10)

因此，根据轨道中线横向偏差、高程偏差测量标准差，直接计算出轨道中线横向偏差的测量中误差ms和高程偏差的测量中误差mz

(11)

轨道平顺性主要包括轨向和高低两个方向，是影响行车的重要指标，同时，根据波长的不同，又分别包括10 m弦短波，5/30 m弦中波及150/300 m弦长波等[16]。

在绝对测量中通过轨道三维坐标计算10 m弦短波较为复杂，通常采用线路横向偏差和高程偏差进行计算

(12)

式中，f(l)为轨道横向偏差或高程偏差，mm；k为对应点里程，m。

对于同一测站内，设站误差相同，被直接消去；对于不同测站，经过搭接处理后，设站误差间接被消除，因此，分析10 m弦平顺性精度时，不考虑设站误差，Dss和Dzz在k，k-5，k+5处相互独立的，可得到10 m弦不平顺的标准差为

(13)

其中，当D10为轨向时，D为Dss，当D10为高低时，D为Dzz。

同理，根据5/30 m弦的计算通式[17]

(14)

可得到5/30 m弦的标准差

(15)

根据150/300 m弦的计算通式[17]

(16)

在长波计算中，两测点相距150 m，处于不同测站内，设站误差不能忽略；由于两测点处于不同设站，测量相互独立，测量标准差为

(17)

评价轨道精调质量主要依据有：(1)绝对位置是否符合要求，如中线横向偏差和左右轨高程偏差；(2)相对点位是否符合要求，如长短波的轨向偏差和高低偏差。依据测量仪器示值误差符合性评定的基本要求[18]，应有

(18)

式中，U95为示值误差的测量不确定度(95%的置信度，U95≈2 m)；MPEV为被评定量最大允许误差的绝对量值。

以轨道实测中线与设计中线的横向允许偏差10 mm为例[3]，根据仪器符合性评定的基本要求，线路横向偏差测量中误差不应大于1.67 mm。而根据测量中误差计算公式，当测量距离为80 m，基于0.5″全站仪绝对测量模式的线路横向偏差的测量中误差ms为0.85 mm(公式(10)、公式(11))。若仅考虑横向偏差，以测量中误差ms=1.67 mm为限，全站仪最大测量距离可达293 m(采用牛顿迭代法使ms逼近1.67)。同理，其他项目的控制标准、测量中误差理论允许值、测量中误差理论值(测量距离80 m)及最大测量距离，如表1所示。

基于表1数据，基于0.5″全站仪的绝对测量模式能够满足轨道中线点位平面、高程±10 mm的控制精度要求，也能满足150/300 m长波轨向和高低±10 mm的控制精度要求。绝对测量模式对轨道中短波控制能力相对较差，10 m弦的轨向和高低恰好能满足要求，5/30 m弦的轨向和高低却不能满足要求，在实际的轨道精调中，特别是在环境不稳定、仪器校准不到位等情况下，常导致轨向高低的中短波控制能力不足，精调后TQI轨道质量达不到要求。

表1 轨道验收标准与测量中误差

3 复合测量模式与线路试验

基于以上分析，为弥补绝对测量短波平顺性精度与长波平顺性和绝对定位精度的不匹配，在绝对测量的基础上，引入短波平顺性测量精度好、测量效率高的相对测量。首先，减少绝对测量采样密度，按1板1测的方式测量线路中线三维坐标、横向偏差、高程偏差等轨道外部几何状态信息。同时采用相对测量采集线路相对轨迹，包括轨距、超高、轨向、高低等轨道内部几何状态信息。即：测量时采用相对+绝对的复合测量模式，数据分析时对绝对测量成果和相对测量成果进行数据融合。

陀螺仪测量的轨道平面相对轨迹为曲线τ，由于陀螺仪自身的漂移(主要包括偏差重复性、偏差稳定性、随机游走等)特性的测量误差随时间累积[19]，曲线τ逐渐偏离实际曲线。其基本思路是：取相对测量中曲线τ相对于定位点(如qm和qm+k)的相对偏差信息与绝对测量中绝对偏差信息进行数据融合，如图3所示。

图3 复合测量模式数据处理

曲线τ上某点qi(xi，yi)相对于定位点所对应的qm(xm，ym)和qm+k(xm+k，ym+k)的相对偏差Δyi为

(19)

绝对测量中，Qi(Xi，Yi)位于定位点Qm(Xm，Ym)和Qm+k(Xm+k，Ym+k)之间，而Qi(Xi，ΔYi)位于直线QmQm+k上，因此

(20)

将相对轨迹的相对偏差和绝对偏差进行叠加

Yi=ΔYi+Δyi

(21)

因此，可得到同时具有相对平顺性和绝对位置性的逐枕的轨道偏差数据Qi(Xi，Yi)。基于以上计算方法，在数据采集完成后，将绝对测量数据导入相对测量软件的轨道精调分析模块，对相对测量成果和绝对测量成果进行数据融合，得到中短波平顺性与相对测量一致，长波平顺性及绝对位置与绝对测量一致的成果数据，模拟调轨，分析调整量，进行线路试验。

3.1 线路试验情况

仪器：客运专线轨道测量仪1台；0级轨道检查仪1台；Leica TS60全站仪1套。

环境：温度15～22 ℃；气压1 002～1 007 hPa；湿度45%～55%。

场地：高速板式无砟轨道，满足以下要求。

(1)沿线建立永久性CPⅢ控制网，满足《高速铁路工程测量规范》(TB10601—2009)[20]的要求。

(2)试验前对控制网进行了复测，残差控制在0.5 mm以内。满足《高速铁路工程测量规范》(TB10601—2009)第3.5节、第4.7节的要求。

(3)标准试验线2段，位于同一段圆曲线的两侧，位置上相对于圆曲线的中点对称，长度各1 km，其中直线340 m、缓和曲线310 m和圆曲线350 m。

3.2 试验方法(复合测量模式)

(1)采用0级轨道检查仪测量线路，采集线路轨距、超高、轨向、高低等轨道内部几何状态参数，评价调轨前线路的TQI。

(2)采用客运专线轨道测量仪，按稀疏采样方式采集线路定位数据，即全站仪在三角架上设站后测量小车上的棱镜，全站仪每站最大测量距离120 m，过程中仅采集每块轨道板第1根轨枕的线路横向偏差、高程偏差、超高偏差、轨距偏差等定位数据。

(3)将测量仪采集的绝对测量数据和0级轨检仪采集的相对测量数据一同导入相对测量软件，进行数据融合，模拟调轨，打印调整量报表。

(4)根据调整量报表，更换轨距挡块和轨下垫板。

(5)采用0级轨道检查仪对线路进行复测，分析调后线路的TQI。

3.3 对比试验(绝对测量模式)

(1)采用0级轨道检查仪测量线路，评价调轨前线路的TQI。

(2)采用客运专线轨道测量仪按标准采样方式采集线路定位数据，全站仪在三角架上设站后测量小车上的棱镜，全站仪每站最大测量距离80 m，过程中采集每根轨枕的线路横向偏差、高程偏差、超高偏差、轨距偏差等定位数据。

(3)将测量仪采集的逐枕绝对测量数据导入精调分析软件，模拟调轨，打印调整量报表。

(4)根据调整量报表，逐枕更换轨距挡块和轨下垫板。

(5)采用0级轨道检查仪对线路进行复测，分析调后线路的TQI。

如表2所示，复合测量模式的TQI由调前的3.87降到2.47，下降1.4，轨道质量得到明显改善，综合效率0.54 km/h，其中第2步相对测量时间约20 min(4 km/h推行速度)，第3步绝对测量时间约90 min(每10枕采集1次数据，约160枕/km)；而单独绝对测量需要逐枕测量，标准轨枕数量为1 667枕/km，每次设站最大测量距离不大于80 m，测量效率约为0.23 km/h。相比于传统的绝对测量模式，复合测量模式在TQI改善和测量效率提升方面取得较好的效果。