基于积温理论的温室温度混杂系统预测控制
2018-10-20秦琳琳黄云梦
秦琳琳 马 娇 黄云梦 吴 刚
(中国科学技术大学信息科学技术学院, 合肥 230027)
0 引言
现代温室是设施农业的典型代表,温室技术是现代农业技术的重要组成部分,温室环境系统建模与控制是温室技术的核心[1]。为实现温室环境调控,现代温室安装有各类传感器和环境调控设备。根据温室环境调控需要,传感器一般包括温度传感器、湿度传感器、二氧化碳浓度传感器、太阳辐射强度传感器、风速传感器等,分别用来测量室内外温度、室内外湿度、室内二氧化碳浓度、太阳辐射强度以及室外风速。控制装置主要包括天窗、湿帘、风机、遮阳网等[2]。在中国,温室环境调控设备主要由开关设备和能连续控制但无位置反馈的设备构成。
温室小环境控制经过多年积累,已经取得很多重要成果,目前研究重点主要集中在3个方面:①建立温室温度和湿度模型,包括根据能量平衡和物质平衡建立的机理模型[3-5],以及根据输入输出数据,采用系统辨识方法建立的辨识模型[6-8],由于机理模型未知参数较多,而且多数参数难以确定,部分参数测量需要特殊仪器,甚至部分参数还可能随着温室长期运行发生改变,建模较多采用基于输入输出数据的参数模型[9]。②利用各种先进的智能控制算法进行环境控制,如MIRZAEE-GHALEH等[10]采用模糊控制、FOURATI[11]采用人工神经网络、MARTINOVI等[12]采用专家系统,都是试图避免建模过程,直接设计控制系统。③国内温室混杂系统的研究,通过引用混杂自动机[13]、切换系统[14-15]来解决温室温度建模与控制的问题。混杂自动机控制可以有效解决设备频繁切换的问题,但控制精度有限,切换系统可以与智能控制算法结合[16],提高控制质量。
目前温室调控策略多是着眼于“最优”的气候环境控制[17],但温室温度系统的输入量包括环境调控设备的开关状态以及外界可测不可控的扰动输入,只能通过控制调控设备开关对温室温度进行调控,但扰动输入会使温度控制无法始终满足设定值。如果只考虑控制精度会大大增加调控成本,为减少调节温室温度带来的能源浪费,需要优化温度调控设定值[18]。
本文利用切换系统的思想来解决温室温度系统的建模和多输入预测控制问题,在每个控制时刻获得温室多个设备的控制序列,因此优化性能指标的求解是一个NP-hard问题[19]。引入积温控制思想[20-21]对预测控制设定值进行优化,采用双周期规划积温目标,根据积温和当前温度动态调整预测控制设定值,以减少能耗,避免设备频繁切换。
1 温室温度系统建模
由于温室温度调控设备主要是由开关设备以及能连续调节但无位置反馈设备构成,设备(如天窗、湿帘、风机、遮阳网等)状态一般是离散变量,而室外环境变量(如太阳辐射、室外温度、室外湿度、风速等)与室内环境变量(室内温度、室内湿度等)是连续变量,因此温室温度系统是一个典型的混杂系统。温室温度系统中的室外环境变量是可测不可控的扰动输入变量,与环境调控设备共同影响温度系统的动态特性。设备状态不同逻辑组合会使系统产生不同的动态特性,一种确定的设备状态即可视为一个子系统,温室系统的建模也可转换为对所有子系统的建模。
1.1 模型选取
模型选择采用线性自回归滑动平均(Auto-regressive moving average with exogenous variable,ARMAX)模型
(1)
其中
(2)
q-1y(k)=y(k-1)
式中k——采样时刻序号
q-1——移位算子
y(k)——第k个采样时刻室内温度
ui(k)——第k个采样时刻室外环境因子
nbi——各室外环境因子量阶次
ndi——噪声阶次
e(k)——均值为零、有界、不相关的平稳随机序列
温室环境变量众多,冗余的信息条件会降低模型精度,减慢收敛速度,故需要分析输入变量以简化模型。采用相关分析技术选取与温度系统最相关的输入变量。皮尔逊相关性系数ρX,Y计算公式[22]为
(3)
式中E——数学期望
1.2 模型结构确定
模型阶次n是模型残差平方和γ(n)的函数,模型阶次递增γ(n)下降,且在n=n*处有拐点,n*为实际阶次,根据拐点实现模型定阶[23]。
γ(n)=(y-X)T(y-X)
(4)
为了更直观判断,利用统计假设检验判断拐点,引入统计量
(5)
式中N——数据长度
f服从F(f1,f2)分布,2个自由度分别是:f1=3(n2-n1),f2=N-3n2,当阶次是逐阶递增,则f1=3,当数据长度足够长,f2≈N。
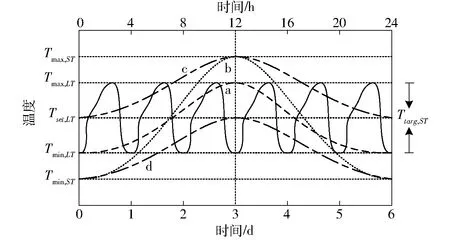
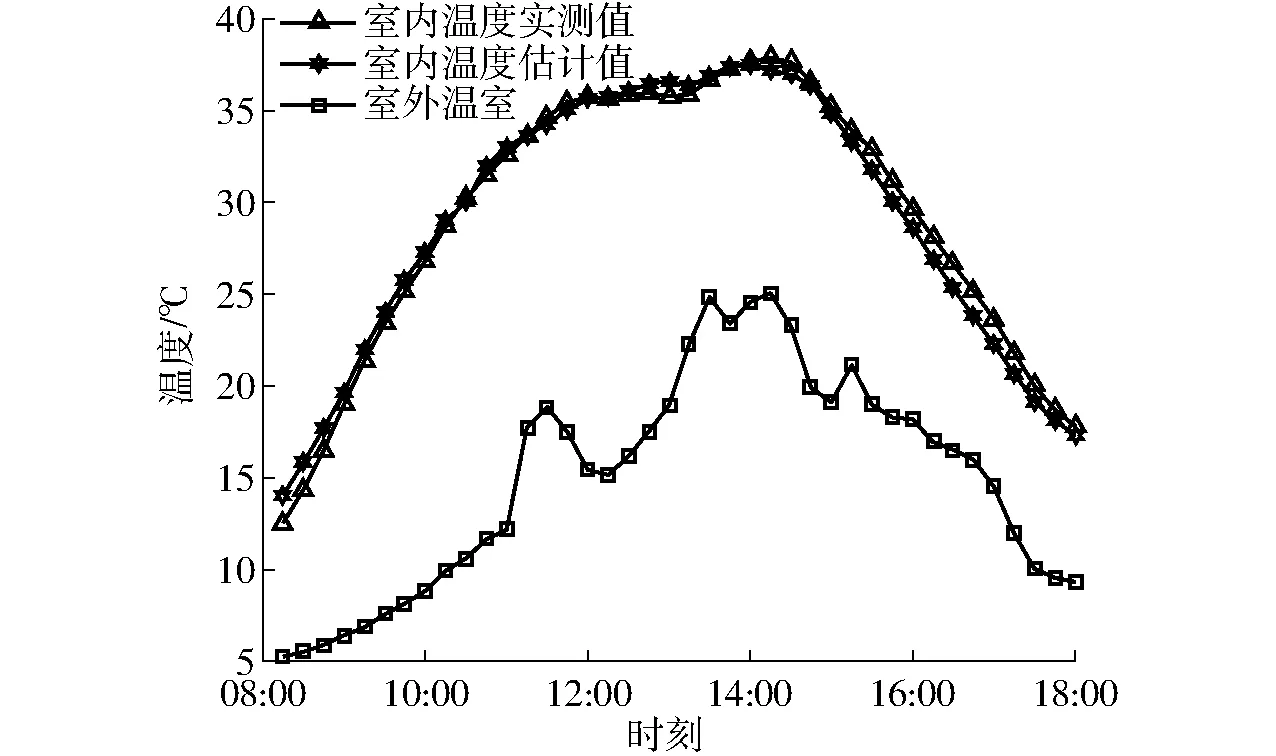
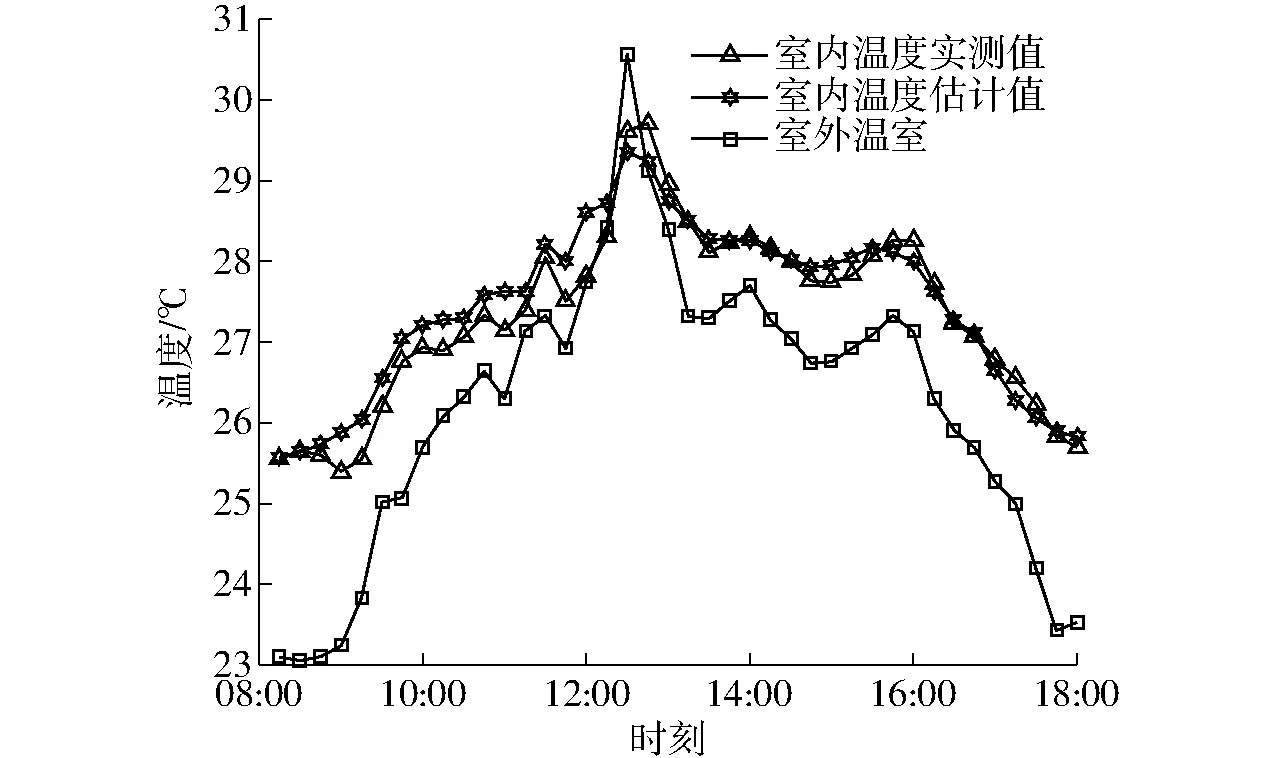
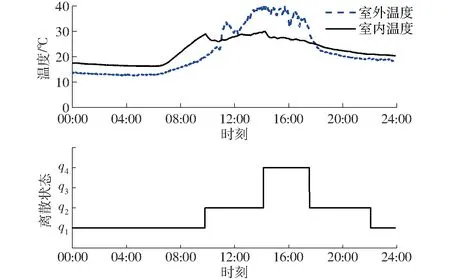
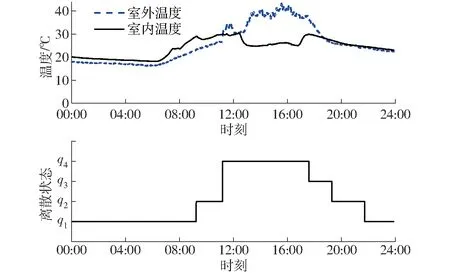
根据F检验,判断当阶次从n1增加至n2时,γ(n)的减小是否显著。引入统计量α,f*为f1、f2确定时的F分布临界值,若f>f*,则认为在α风险水平下γ(n)的变化是显著的,反之亦然。按照上述分析,可知第一次出现f 为防止因辨识数据过多导致饱和,优先考虑新数据对模型的影响,采用带遗忘因子λ的最小二乘增广递推算法[24] (6) 式中L(k)——k步估计观测向量 Y(k)——k步模型输出 λ——遗忘因子,λ∈(0,1] 为检验模型精度,验证模型输出与实际输出的拟合效果,采用均方根误差(Root mean square error,RMES)作为指标[25] (7) 式中yk——k采样时刻的实际输出 eRMSE——均方根误差 预测控制基本思想是在每一个采样时刻,使用当前时刻的实测输出和模型的多步预测输出,通过极小化有约束的目标函数,获到当前和未来有限时段的控制量序列,仅使用控制量序列第一个值作为当前控制量。在下一采样时刻检验实际输出值,重新计算预测输出,计算控制量,形成了闭环反馈控制。 预测控制引入到温室温度控制中,每个采样周期优化的应是预测域中的状态切换序列。预测控制算法性能指标函数为 (8) (9) (10) (11) (12) y(t|t)=y(t) (13) 式中Spt——预测控制设定值 P——预测步长 R——子模型个数 σjk——第j个子模型状态,0表示关闭,1表示开启,σjk={0,1} y(t)——当前t时刻输出 y(t+k|t)——t时刻对t+k时刻的预测输出 在预测控制序列求解过程中,由于系统输入包括可测不可控的室外环境因子扰动,而扰动序列中[ut+1,ut+2,…,ut-d+k]是未来时刻室外环境因子,需要对其进行预测。采用滑动灰色预测算法[15]预测未来短时间室外环境因子。 每个设备的动作序列为待求解的控制量,每一步预测输出中,不同时刻不同设备控制序列是乘积关系,性能指标函数阶次为RP。这个高阶多项式还是一个非确定性多项式(Non-deterministic polynomial,NP),所求问题是NP-hard问题[19],且待优化问题中,未来的决策受之前状态的直接影响,即不满足动态规划算法的无后效性原理,无法使用动态规划解决。采用最优化剪枝穷举法来求解待优化问题。最优化剪枝算法实施步骤如下: (1)按预测步数将问题分解成P个子问题:J=J1+J2+…+JP。 (2) 计算切换序列的损失函数J(i),i=1,令最小损失函数minJ=J(i),i=i+1。 (4) 重复步骤(3),直到遍历所有切换序列。 在切换系统中运用预测控制,在每一采样时刻,设定值是确定的,得到的控制量是切换序列,而系统在不可控的室外环境因子强力扰动下,输出波动较大,若采用固定设定值,则系统会频繁切换,增加设备损耗。一般温室温度控制是将室内温度控制在一个区间内,且目标区间的取值也不是固定的。 作物在极端温度下生理结构、光合作用会受到损害,积温控制理论认为,在极限温度之内,作物的生长发育与一段时间内其所处环境温度的积累有关。作物光合反应是瞬间过程,而光合同化物向干物质转换是动态过程,有缓冲能力。不同作物的缓冲能力有差异,为防止积温对作物生长发育造成影响,需要规划积温控制的积温周期与积温设定值。 本文采用双周期积温控制方法,长周期设为6 d,短周期设为1 d[20]。作物在长周期期间积温总量期望为Tset,LT,长周期积温有效区间为[Tmin,LT,Tmax ,LT],作物可承受极限温度区间(即短周期积温区间)为[Tmin,ST,Tmax,ST],短周期积温期望是非固定的,温度在允许范围内波动的同时,其平均温度需要满足长周期规划。 双周期积温规划图如图1所示,图中实线表示长周期规划曲线,虚线表示短周期规划曲线。图中曲线a是常见的短周期温度曲线,所有温度都在长周期有效积温区间内,平均温度为Tset,LT;曲线b则是以极限温度作为界限,平均温度为Tset,LT,温度波动范围很宽;曲线c平均温度为Tmax,LT,曲线d平均温度为Tmin,LT,都满足短周期规划,也都可作为长周期规划的其中1 d。Ttarg,ST表示短周期规划日平均温度目标区间。 作物生长发育除了与积温关系密切,其形态学特征是受昼夜温差(Difference between day temperature and night temperature,DIF)的影响,温差为正会促进植株长高,反之会抑制植株株高,根据作物生长需求调节DIF值。 图1 双周期积温规划Fig.1 Dual-cycle temperature integration planning 长周期积温控制策略是一种事后补偿过程,并非在控制过程前确定整个周期内最佳的温度设定值,而是在长周期最后1 d补偿周期前5 d的平均温度偏差。故未来24 h积温目标可表示为 (14) (15) 令 (16) [Tset,L,Tset,H]即为未来24 h温度控制目标,前(P-1)日平均温度和直接决定未来24 h的温度控制设定值。若前(P-1)日平均温度已满足长周期积温规划,则未来24 h设定值区间会放宽,如图1曲线b;若前(P-1)日平均温度低于长周期积温规划设定值,则未来24 h设定值会升高,如图1曲线c;若前(P-1)日平均温度高于长周期积温规划设定值,则未来24 h设定值会降低,如图1曲线d。积温在长周期积温要求的同时,短时温度也不能超过作物可承受极限温度范围。此外,设定值范围应合理,不应集中在过高或者过低区域,以长周期积温上下限中点Tmid,LT=(Tmax,LT+Tmin,LT)/2作为积温目标Tset,L的上限,作为积温目标Tset,H的下限,Tmin,ST≤Tset,L≤Tmid,LT,Tmid,LT≤Tset,H≤Tmax,ST。 所以有 (17) (18) 预测控制积温设定值规划为 (19) 式中Treal——当前室内温度 设定值的确定还应考虑DIF值,研究表明试验温室种植的番茄作物在开花前保证6.0~8.0℃的DIF可以促进生长[26]。 实验温室位于安徽合肥中国科学技术大学西区信息科学技术学院,面积82 m2,东西走向,东西长12.2 m,南北跨度8.2 m。温室内安装有温湿度传感器、太阳辐射仪器、CO2浓度传感器,室外设有小型气象站,包括温湿度传感器、太阳辐射仪器、风速风向传感器用于测量环境参数。 实验温室中温度调控的设备包括天窗、风机和湿帘,结合温室控制经验,这3种设备可将系统分为保温、自然通风、强制通风与湿帘-风机4种状态,状态如表1所示。 表1 设备状态Tab.1 Meaning of discrete states 表1中设备状态表示风机、湿帘和天窗3个设备的开关状态,0表示设备关闭,1表示设备打开,如自然通风模式下设备状态为“001”表示δ1=0,δ2=0,δ3=1,即风机关闭、湿帘关闭、天窗打开。辅助变量的值是计算设备状态的二进制值,即Δ=4δ1+2δ2+δ3,利用辅助变量可实现状态的编码。 4.2.1相关性分析 不同离散状态下输入变量与输出相关性分析结果如表2所示。 表2 室外环境因子与室内温度相关系数Tab.2 Correlation coefficients between outside environmental factors and inside temperature 注:x1为室外温度,x2为室外湿度,x3为风向,x4为风速,x5为太阳辐射强度。 表2中相关系数绝对值越大说明相关性越强,正值表示两个变量正相关,负值表示两个变量负相关。由表2数据可知,在保温模式下,室外温度、室外湿度、太阳辐射强度与室内温度相关性较强,因此选取室外温度、室外湿度、太阳辐射强度作为主要输入变量。在自然通风、强制通风和湿帘-风机模式下,室外温度、室外湿度、太阳辐射强度以及风速与室内温度相关性较强,因此选取室外温度、室外湿度、太阳辐射强度与风速作为主要输入变量。 4.2.2模型阶次确定 从阶次n=1依次计算γ(n),γ(1)=0.041 4,γ(2)=0.018 9,γ(3)=0.018 6。 当n1=1,n2=2,N=136时,有 当n1=2,n2=3,N=136时,有 所以模型阶次为二阶,为进一步确定子阶,假设na=nb1=nb2=nb3=nb4=nc=15,nd1=nd2=nd3=nd4=1,根据假设检验确定子阶与时延结果为:na=2,nb1=1,nb2=1,nb3=2,nb4=1,nc=0,nd1=1,nd2=2,nd3=2,nd4=10。 4.2.3辨识结果 保温模式下辨识结果为:a11=-1.367 3,a12=0.562 2,b11=0.005 6,b12=0.055 6,b131=-0.055 3,b132=-0.164 9。 自然通风模式下辨识结果为:a21=-1.195 8,a22=0.427 6,b21=0.189 6,b22=0.001 3,b231=0.086 6,b232=0.064 8,b24=-0.064 4。 强制通风模式下辨识结果为:a31=-0.682 5,a32=0.282 6,b31=0.684 6,b32=0.017 3,b331=-0.180 0,b332=0.073 5,b34=-0.057 3。 湿帘-风机模式下辨识结果为:a41=-1.033 6,a42=0.457 7,b41=0.277 5,b42=-0.059 7,b431=0.268 7,b432=-0.155 8,b44=-0.178 8。 4.2.4模型预测结果 分别在2017年3月9日(保温)、2017年3月22日(自然通风)、2017年8月10日(强制通风)、2017年8月4日(湿帘-风机)的08:00—18:00对温室温度系统4种子模型建模,效果如图2~5所示。 图2 保温模式模型拟合效果(RMSE为0.706 4℃)Fig.2 Fitting result of temperature under preservation mode(RMSE was 0.706 4℃) 图3 自然通风模式模型拟合效果(RMSE为0.305 5℃)Fig.3 Fitting result of temperature under nature ventilation mode(RMSE was 0.305 5℃) 4.2.5预测控制结果 若未引入积温,设定值为固定值。实验时间为2018年3月27日,取设定值为 预测控制效果如图6所示,图中系统给出1 d室内外温度以及离散状态切换过程。 图4 强制通风模式模型拟合效果(RMSE为0.335 8℃)Fig.4 Fitting result of temperature under forced ventilation mode(RMSE was 0.335 8℃) 图5 湿帘-风机模式模型拟合效果(RMSE为0.277 8℃)Fig.5 Fitting result of temperature under curtain-fans mode(RMSE was 0.277 8℃) 图6 预测控制效果Fig.6 Predictive control results 室内最低温度为17.7℃,比设定值下限24.0℃低26.3%,这是由于实验温室设备控温能力有限,没有主动加温装置,故不能保证室内温度始终在设定范围内;最高温度28.9℃,低于设定值上限29.0℃。在设备能控范围内(08:00—18:00时间段),有76.6%的时间室内温度控制在设定范围内,可看出预测控制能有效控制室内温度。 使用双周期积温规划预测控制设定值,取TDIF=6℃,Tmin,LT=22.0℃,Tmax,LT=26.0℃,Tmin,ST=10.0℃,Tmax,ST=30.0℃。实验时间2018年3月31日,前5 d日平均气温如图7所示。 图7 2018年3月26—30日5 d平均温度曲线Fig.7 Average daily temperature curve of five days from March 26 to March 30 of 2018 设定值规划为 加入积温优化设定值后,控制效果如图8所示。室内最低温度为16.3℃,比设定值下限Tset,L低22.5%;室内温度最高为Tset,H=30.0℃。在设备能控范围内,室内温度全部被控制在设定值范围内。 图8 积温优化设定值预测控制效果(2018年3月31日)Fig.8 Predictive control results optimized by accumulative temperature method 积温第2个实验时间为2018年4月10日,前5 d日平均气温如图9所示。 图9 2018年4月5—9日5 d平均温度曲线Fig.9 Average daily temperature curve of five days from April 5 to April 9 of 2018 设定值规划为 加入积温优化设定值后,控制效果图如图10所示。室内最低温度为18.1℃,比设定值下限Tset,L低26.2%;室内温度最高30.4℃比设定值上限Tset,H高1.3%。在设备能控范围内,有95.6%的时间室内温度控制在设定值范围内。 图10 积温优化设定值预测控制效果(2018年4月10日)Fig.10 Predictive control results optimized by accumulative temperature method 对比图6与图8、图10,可见引入积温理论动态调整设定值,将设定值范围放宽可以有效减少设备切换次数。 (1)基于温室温度系统同时包含离散状态(设备开关)与连续状态(各环境因子)的混杂特性,利用切换系统建模方法,根据设备状态将温室温度混杂系统分为4个子系统,分别对4个子系统建模。首先选取室外环境因子中与温室温度相关性最高的室外温度、室外湿度、太阳辐射强度和风速作为输入变量,使用ARMAX模型描述系统,利用统计假设检验方法确定模型阶次为二阶。分别在4个子系统下,采用带遗忘因子的增广递推最小二乘法辨识模型参数,并检验模型精度。 (2)使用建立的切换系统模型设计预测控制器,引入双周期积温法调整预测控制设定值,避免设备频繁切换。待求解问题为高阶NP-hard问题,采用最优化剪枝法优化求解过程。最后在实际系统验证预测控制算法,实验证明温室内温度在设备调控范围内可以有效控制在设定值范围内,并且引入积温理论规划预测控制设定值可以减少设备切换次数。1.3 辨识方法与模型检验
2 温室温度系统的预测控制
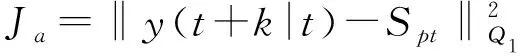
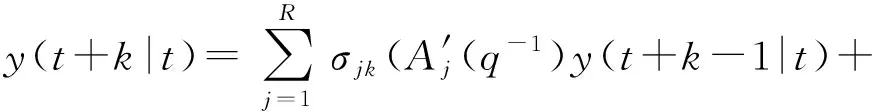
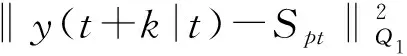

3 积温理论优化温度设定值


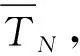
4 实验分析
4.1 实验材料与方法

4.2 建模结果与分析







5 结论
