基于stm32小型四轴飞行器PID参数整定
2018-10-19广东理工学院罗昌恩张国林
广东理工学院 罗昌恩 张国林 戴 毅
1.现状
四轴飞行器有着小巧灵活,稳定可靠,成本可观姿态丰富,模块化程度高的特点,此飞行器是一款备受关注的垂直起降无人机,有不错的市场前景,日趋完善的控制技术让无人机能完成更加出色的飞行姿态,满足更多领域的需求。
2.四轴飞行器的设计
2.1 飞控硬件模块

表1 硬件
2.2 控制原理
在姿态控制运算上,国外科研机构通过他们的研究成果表明:PID控制算法相比诸多高级控制算法,如非线性控制、预测控制、滑模变控制等,对模型精度要求大大降低,所以将PID控制算法应用于姿态控制上效果更加理想。
飞行姿态控制主要有智能控制算法与PID控制算法两大种类,前者相比后者对微处理器要求较高,所以基于STM32为核心的四轴飞行器使用的PID控制算法是四轴飞行器目前的最优算法。
其中PID控制针对无人机作用如下:
比例P能够迅速对误差信号进行响应,将误差比例放大作为控制量的输出。
积分I主要用于消除无人机系统静态误差,提高追踪精度。
微分D主要是提高无人机系统响应速度,增强无人机系统稳定性,通过误差变化趋势提前产生控制量。
PID控制器结构简单,能对控制量偏右起到有效的抑制作用。
四轴飞行器的飞行原理:前后桨间隔安装,各桨旋转方向与相邻螺旋桨相反,提供相同的动力方向(图1)。
根据四轴飞行器的特殊性,PID控制算法中位置式相比增量式存在不少缺陷:首先是计算量大,而且计算量会随着时间推移而逐渐增加,受过去状态影响较大,计算过程过于冗杂;其次,保留所有采样值占用空间过于庞大。为保持飞行稳定、降低调节PID参数达到理想值的难度而优先采用增量式PID控制算法。

图1 四轴飞行器控制流程图
增量式PID控制是指将变化量△uk作为控制量输出。根据实际调节情况,通过最近几次采样结果计算求出控制量,经综合因素考虑优先采用最近三次的结果进行计算。实验证明控制算法中增量式PID与位置式PID相比计算量较少,被控量不会产生大幅度变化,执行机构工作状态相对稳定,且容易实现无扰动切换。
3.PID参数整定
3.1 PID参数整定过程
通过两个轴来分别实现两个电机控制功能,它们各自调节十字模型四轴飞行器俯仰和横滚姿态,这种调节方式下两个轴不会因耦合使之前的PID调节参数变成伪参数。按照增量式PID整定原则,首先确定P参数值范围,让控制处于近似等幅震荡的最佳位置。下表给出了P参数调试的基本过程。

表2 P参数整定表
根据四轴飞行系统确认P参数值大小后,D参数设的调节过程

表3 D参数整定表
最后确定微分D参数在0.16左右时,PID控制能够迅速响应和抑制震荡。确定I参数。由于整个四轴系统控制量与系统的静态误差相比而言较小而油门应控制在50%的范围,所以将积分项幅值范围限制在100以内避免发生积分超调。最后根据姿态变化规律范围,确定I参数应设定在0.1左右。
3.2 PID整定步骤(根据数据模型整定)
调整比例项P可增减系统响应时间来改善系统快速性,调整积分项I有助于提高系统稳态精度、降低系统震荡,调整微分项D可改善系统动态性能。
在基于stm32四轴调整PID控制过程中,PID系数调整步骤如下:
(1)将积分项I参数值与微分项D参数值置零,改变比例项P参数值从零逐渐增大。当比例项P参数值到达某一数值时,四轴飞行器能抵抗外部作用力,同时会产生正弦波形震荡。减小比例项P参数值则使四轴飞行器无法抵抗外部作用力。但若继续增大比例项P参数值则会产生过大震荡,此时对比例项P参数值进行一加一减的方法以确认是否达到较好的正弦波形震荡即可基本满足要求,当条件满足时可以进入调整积分项I和微分项D系数。
(2)比例项P参数值确定后在抵抗外部作用力会产生正弦波形震荡,把积分项I参数值逐渐增大到某值时,会抑制前一步骤中产生的震荡。继续修改积分项I参数值,使四轴受到外力作用后产生的正弦波形震荡应尽可能小,此时可确认为达到理想值。
(3)保持积分项I参数值,微分项D参数值为零,增加比例项P参数值,使四轴无人机系统控制过程中能够产生快速响应,且正弦波形震荡减小到可以维持基本平衡状态。
(4)设定比例项P参数值与积分项I参数值后,调整微分项D参数值,使四轴无人机系统达到较为理想的稳定平衡快速状态。
增量式PID各项参数需要不断调试,反复试验总结控制规律才能得到最终比较理想的快速稳定效果。
3.3 参数引起的响应曲线变化

表4 不同PID参数下的系统响应曲线变化
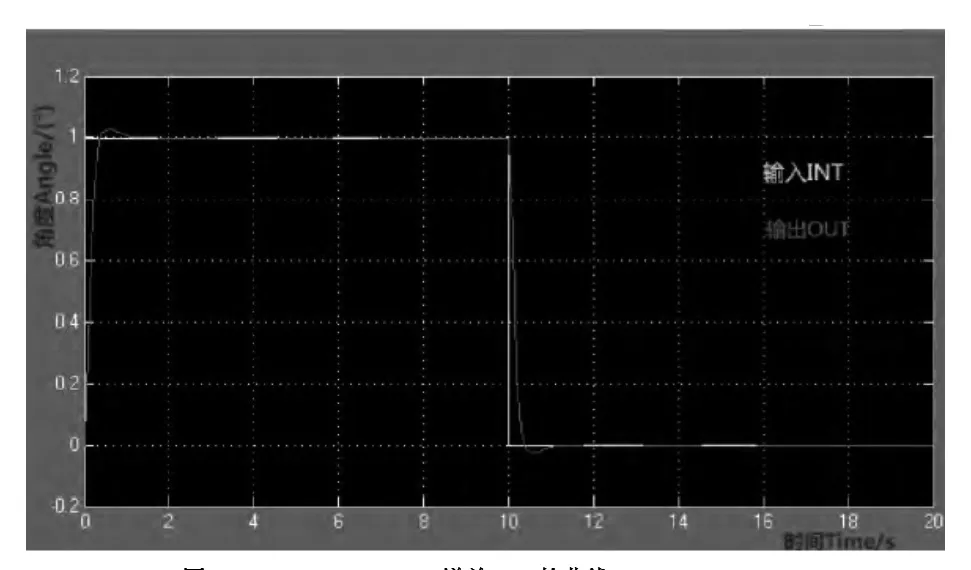
图2 Kp=15,Ki=3,Kd=3,增益K=3的曲线
由上表数据可知,第1组数据中超调量为17.4%,上升时间为0.74s;第2组中超调量为5.2%,上升时间为0.74s;第3组中超调量接近为0,上升时间为1.5s;第4组中超调量为2.7%,上升时间为0.38s。
通过第1组,第2组和第3组数据的对比可知,当增益K=1,超调量较大,当增益K=1.5,超调量明显低于增益K=1时的值,系统响应曲线在变化较小的情况下变化趋势不明显,说明在四轴飞行器结构不变的条件下,采用增量式PID可以使四轴飞行器达到稳定平衡快速的飞行状态;当增益K=3,超调量接近为0,明显低于增益K=1和增益K=2时候的数值,可以看到四轴飞行系统响应曲线和结构在变化较大时有明显的变化趋势;由图2和第4组数据,PID参数重新调整使飞行系统得到较为理想控制效果。
多次调试数据试验显示,通过试凑法进行反复试验,可调整增量式PID参数达到理想响应曲线变化,实现更加良好的控制效果。
3.4 算法分析
由于基于STM32的四轴无人机系统存在的不稳定性较多,所以根据实质的需求采用以下算法以增强该稳定性:
(1)分段比例控制设计:通过多次的实验证明单纯PID控制无法满足复杂的控制系统要求,可引用分段比例控制优化四轴飞行器的算法设计。在飞行器姿态角的调整过程中,俯仰角可调整范围为±90°,横滚角可调整范围为±180°。分段比例控制是通过判断当前姿态角和目标姿态角的差值确认值域来实现动态调整PID控制器中比例P系数。常用的分段范围有±5°、±10°、±20°等,由此可知,比例系数Kp与分段差值成正比例关系。由于四轴飞行控制系统难以建立合理的数学模型,受外部因素影响,如电池电压、整体的重量以及电机的输出不稳定等,因此比例系数P的确定需要多次反复实验。
(2)死区:设立这一步骤是用来消除负反馈误差值,负反馈误差值是通过PID控制器设定值和过程变量也即是反馈量两者的相减关系来反应的,由前者减去后者得到。PID控制器输出值变化过程为:当误差值处于系统设定的死区范围外,死区的输出为0,比例、微分环节输出值为0,而积分环节不变。当误差值处于动态设定的死区范围外时,死区输入与输出为线性关系,根据PID控制律进行调节。
(3)积分分离:采用积分主要作用是校正稳态误差改善系统静态特性。控制过程当中产生扰动或者设定值变化时,系统输出短时间有明显偏差,往往容易产生较大超调量和长时震动,在温度、成分等迟缓反应中更为明显。我们通常选用积分分离避免上述情况发生。
(4)过饱和PID控制:如果控制器长期存在偏差或偏差过大,系统就会出现饱和现象,所做PID控制调节就没意义。所以,为了防止系统进入饱和状态时间过长,最好在额定转速全导通状态下工作。
4.结语
本文主要基于STM32的四旋翼建模,对PID参数通过波形图的仿真以及对其PID整定过程以及整定步骤的总结进行分析;实验结果表明,通过增量式PID对四旋翼进行控制,在调节参数方面通过试凑法与仿真结合的方法可以得到较为理想的控制效果,同时在增量PID上添加分段比例控制,死区,积分分离,过饱和PID控制这几种算法可增加四旋翼的稳定性。
引文
①郭凯.基于STM32单片机的四轴飞行器设计及控制技术的研究[D].安徽理工大学,2016,6.
②陈振兴.基于STM32的微型四轴飞行器研究与设计[D].河北工业大学,2013,12.
③王东平.基于嵌入式的四轴飞行器控制系统研究与设计[D].华侨大学,2013,3.
④杨述斌.基于实时操作系统的小型四轴飞行器设计[D].武汉工程大学,2017,2.
⑤毕嘉诚,陈维民,于晓磊,谢光辉.基于四轴飞行器的串级PID控制算法与建模[D].哈尔滨理工大学,2016,11.
