黑土区土壤水分特征曲线模拟及模型优选

2018-10-19王子龙常广义姜秋香陈伟杰林百健

东北农业大学学报 2018年9期

王子龙，常广义，姜秋香，付强，陈伟杰，林百健

（东北农业大学水利与土木工程学院，哈尔滨 150030）

土壤水分特征曲线是模拟土壤水分和溶质运移重要输入参数，广泛应用于地下水补给、农业与土壤化学、水土保持等领域，可反映土壤孔隙分布状况[1-3]。

测定土壤水分特征曲线费时长、成本高、耗费人力，常用土壤水分特征曲线模型有Brooks-Corey（BC）[4]，Gardner[5]、van Genuchten[6]（VG）及Kosugi[7]、Fredlund 和 Xing[8]、Dual-porosity模型[9]等。土壤传递函数模型分为点预测模型和参数预测模型[10]。点预测模型利用田间含水量33 kPa、凋萎含水量1 500 kPa和土壤水力性质构建函数关系；参数预测模型基于模型参数与物理性质（如土壤质地、有机质、颗粒组成等）构建函数关系。土壤传递函数模型研究主要有线性和非线性拟合、人工神经网络[11]等方法。土壤传递函数模型成果有Vereecken[12]模型，利用土壤中颗粒组成、有机碳等与VG模型参数建立关系式，Cosby[13]和Saxton[14]模型利用颗粒组成与实测土壤水分特征曲线参数作回归分析，姚姣转等在VG模型基础上建立科尔沁沙地土壤传递函数等[15]。

比较分析土壤水分特征曲线传递函数模型和经验模型预测能力，如Woston等比较21种土壤传递函数，结果表明点预测模型模拟精度优于参数预测模型[16]；Kern分析对比6种土壤传递函数模型，发现Rawls模型预测精度最高[17]；Tietje等评价13种土壤传递函数预测效果，结果表明Vereecken模型对土壤水分特征曲线预测值与实测值偏差最小，模拟精度最高[18]；Matlan等对比4种经验模型，结果表明MG模型对不同质地土壤土壤水分特征曲线模拟效果最好[19]；丁新原等利用VG和Gardner模型模拟塔里木沙漠公路防护林SWCC，发现VG模型模拟精度高于Gardner模型[20]。目前，土壤水分特征曲线模型对比研究较多，但模型普适性和精确度依赖土壤类型，对比分析特定土壤适应性尤为必要。

本文以松嫩平原黑土区黑土为例，利用VG、BC、LND、MG 4种土壤水分特征曲线模型模拟不同质地黑土土壤水分特征曲线，对比分析4种经验模型模拟精度，选取最优模型。研究结果为松嫩平原黑土区土壤水分特征曲线预测提供可靠模型和技术支持。

1 材料与方法

1.1 研究区概况

研究区处于松嫩平原黑土区南部黑龙江省哈尔滨市（见图1），位于东经125°42'～130°10'，北纬44°04'～46°40'，全年平均降水量569.1 mm，冬长夏短，属于温带大陆性季风气候。哈尔滨市土壤类型较多，以黑土为主，包括壤土、黏土、砂壤土和砂黏壤土，少量砂土分布江河两岸。黑土土壤养分含量较丰富，是主要耕作土壤，土壤有机质含量高，适宜农作物生长。

图1 研究区地理位置及采样点分布Fig.1 Geographical location and sampling point distribution in the study area

1.2 供试土样采集与测定

选取壤土、砂黏壤土、砂壤土、黏土、砂土5种土壤质地作为供试土样，采样点分布如图1所示。

每个土样采集0～30 cm土层，分别用100 cm3环刀取原状土，自封袋取散土。风干散土土样、过筛2 mm，采用MS2000激光粒度仪分析土壤颗粒，按国际制分类，分为砂粒（粒径0.02～2 mm）、粉粒（粒径0.002～0.02 mm）和黏粒（粒径＜0.002 mm）。采用高速离心机法测定土壤水分特征曲线，分别测定土样1、3、5、10、30、50、100、300、400、500、700、900、1 000、1 200 kPa吸力下体积含水率。干容重采用环刀法测定，土壤样品质地分类如表1所示。

表1 土壤样品质地分类Table1 Textureclassification of soil samples

1.3 土壤水分特征曲线经验模型简介

土壤水分特征曲线经验模型根据参数数量分为三参数模型、四参数模型和五参数模型。研究表明，模型参数越多，实测数据拟合精度更高。

选取4种土壤水分特征曲线经验模型van Genuchten（VG）、Brooks and Corey（BC）、Modified Gardner（MG）、Log-Normal Distribution（LND）模型模拟黑土区土壤水分特征曲线。其中VG模型是van Genuchten在1981年提出应用最广泛模型；BC模型是由Brooks和Corey较早提出的土壤水分特征曲线模型，该模型简单，应用较广；MG模型是由Matlan提出的指数型经验模型，模型参数有明确物理意义，应用范围较广；LND模型是Kosugi提出的对数正态分布模型。4种模型均为四参数模型，具有简单性和普遍使用性等特点。

①VG模型表达式如下：

式中，θ—体积含水率；θs—土壤饱和体积含水率；θr—滞留土壤体积含水率；h—土壤水吸力（cm）；α、n、m为表征模型形状参数，其中α数值上等于进气值倒数。

②BC模型表达式如下：

式中，Se—饱和度。

λ—土壤孔隙尺寸分布参数

③MG模型表达式如下：

式中，b、t为模型参数。

④LND模型表达式如下：

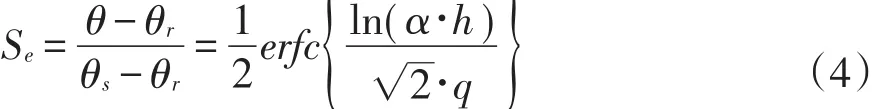
式中，q为模型参数。

4个模型除θs和θr参数外，还包含两个模型参数，分别用P1和P2表示，其中P1单位为kPa、P2为分形参数，如表2所示。

表2 土壤水分特征曲线模型参数Table 2 Parameters of soil water characteristic curve models

1.4 模型参数优化方法

1.41 粒子群优化算法

采用粒子群优化算法（Particle Swarm Optimization，PSO）优化模型参数，模仿鸟群捕食行为提出粒子群优化算法。首先初始化1个种群N，把每个种群中个体假设d维搜索空间中1个粒子，第i个粒子位置和速度分别为Xi=(xi1,xi2,…,xid)和Vi=(vi1,vi2,…,vid)，i=1,2,3…N，每次迭代中，粒子通过自我更新找出最优解，即个体最优解pbest，Pi=(pi1,pi2…,pid)；gbest是整个种群N种中最优解，两个最优解确定后，粒子速度更新和位置更新方程如下：

其中，w为惯性权因子，c1和c2为学习因子，rand1和rand2为0～1均匀分布随机数。

1.4.2 参数模型构建

为精确获得4种模型模型参数，其中饱和含水率θs采用实测数据，以模型拟合体积含水率值与土壤实测体积含水率残差平方和最小为目标函数，求解该非线性最优化问题，即表达式如下：

式中，θobs为土壤体积含水率实测值，θmod为模型拟合值，N为样本数。

1.5 模型精度评价指标

采用均方根误差（RMSE）和Pearson相关系数R作为定量评价指标。

式中，X为体积含水率实测值，Xi为经验模型拟合值。RSME评估模型整体误差；R值反映实测值与模拟值趋势。

2 结果分析

2.1 不同土壤质地土壤水分特征曲线变化趋势

土壤水分特征曲线反映土壤持水能力。通过离心机测定各吸力段下对应土壤体积含水率，绘制不同质地吸力段下体积含水率与土壤水基质吸力变化趋势如图2所示。

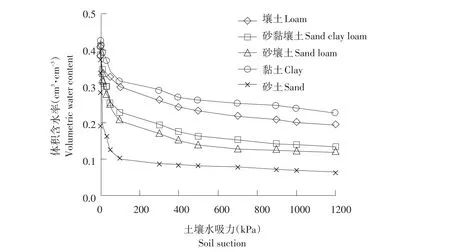
图2 不同质地土壤水分特征曲线Fig.2 Soil moisture characteristic curve of different soil textures

由图2可知，吸力值小于100 kPa时的低吸力段，土壤水分特征曲线急剧下降，变化率大，因为该阶段土壤大孔隙排水占主导；当土壤吸力大于100 kPa时，随着吸力增大，曲线变化率逐渐趋于0，吸力值大于100 kPa时，中高吸力段土壤大孔隙水分在重力作用下排空，仅小孔隙存留水分，毛管力对水分产生作用力，土壤具有较好持水能力，土壤水分特征曲线缓慢降低并趋于平稳。在相同吸力条件下，体积含水率黏土＞壤土＞砂黏壤土＞砂壤土＞砂土，说明黏土持水能力最强，壤土次之，砂土最弱。结合表1不同质地颗粒组成百分含量可知，黏粒含量越高，持水能力越强，由于黏粒粒径较小，黏粒含量越高，小孔隙越多，比表面积越大，对水作用力越强；而砂土砂粒含量较高，粒径较大，比表面积较小，水吸附能力弱。因此降水后砂土大孔隙较多易饱和，形成径流，不利于水土保持。

2.2 土壤水分特征曲线拟合

本文采用VG、BC、MG、LND 4种经验模型拟合5种土壤质地实测土壤含水率数据曲线，基于粒子群优化算法对4种模型参数优化值如表3所示，绘制5种土壤类型土壤水分特征曲线实测值与采用4种模型拟合值关系如图3所示。由图3可知，VG模型对5种土壤拟合值与实测值接近，其中实测值在VG模型曲线上。滞留土壤含水率为0.034～0.092，符合实际土壤滞留含水率。5种土壤质地中黏土饱和含水率和滞留含水率相对较高；砂土饱和含水率和滞留含水率最低，由土壤性质决定。参数n值反映土壤水分特征曲线坡度，土壤水分特征曲线坡度越缓，n值越大，反之越小[23]。砂土坡度最陡，n值不是最小，故认为n为表征曲线形状系数[24]。VG模型参数P1值为0.0375～0.323，则土壤进气值为3.096～26.667，与饱和含水率对应进气值相符。BC模型对砂土和砂黏壤土拟合趋势较好，壤土拟合趋势较差，可较好拟合5种土壤质地曲线。BC模型优化参数中滞留含水率为1.20～5.68×10-4，可知BC模型低估5种土壤质地滞留含水率；模型参数P1值为0.2051～0.9001，土壤进气值为1.1109～4.8756。可知BC模型低估饱和含水率对应进气值。MG模型对5种类型土壤拟合效果较好，实测值在MG模型曲线上。其中除砂土外，对其他4种土壤拟合值更接近实测值，砂土实测值拟合偏差较大。MG模型拟合参数滞留含水率为0.0124～0.1469，与土壤中滞留含水率相近。LND模型优化参数中滞留含水率为0.00012～0.0736。可知LND模型低估壤土和砂黏壤土滞留含水率。LND模型对5种类型土壤拟合值与实测值偏差较小，表明LND模型可较好拟合5种土壤质地土壤水分特征曲线。

表3 不同土壤质地模型参数Table 3 Model parameters of different soil textures

2.3 土壤水分特征曲线模型比较及优选

比较Brooks-Corey（BC模型）、Van Genuchten（VG模型）、Modified Garder（MG模型）和Log-Normal Distribution（LND模型）适用性，对比分析模拟结果。

由表4可知，VG模型对5种类型土壤拟合值与实测值相关系数R为0.996～0.998；BC模型R为0.9547～0.9869；MG模型R为0.994～0.998；LND模型R为0.9820～0.9960，可见4种模型拟合值与实测值变化趋势相似。其中，除壤土外，MG模型对其他4种土壤拟合效果优于VG、BC、LND模型；另外，VG模型对壤土模拟效果最佳。由图3可知，VG、MG、LND 3种模型在低吸力段（0～100 kPa）壤土、砂黏壤土、砂壤土、黏土、砂土拟合值与实测值重合，而BC模型拟合值明显偏离实测值；在中高吸力段（＞100 kPa）VG、MG、BC、LND 4种模型拟合值均在实测值上方。其中BC模型拟合值与实测值偏差较大，而VG、MG、LND 3种模型拟合值略高于实测值，可知VG、MG、LND3种模型对5种类型土壤拟合效果优于BC模型。

由残差平方和值可知，4种模型均可较好拟合不同土壤质地含水量与水吸力间关系，VG、MG模型残差平方和值显著明显低于BC和LND模型，其中BC模型残差平方和值最高，可知MG和VG模型对5种类型土壤拟合效果最佳，BC模型拟合效果最差。从RMSE值来看，MG模型对5种土壤质地RMSE值为0.0033～0.0107；VG模型RMSE变化为0.0039～0.0092；LND 模型 RMSE 变化为 0.0096～0.0114；BC模型RMSE变化为0.0140～0.0250。结果表明，MG和VG模型RSME值明显小于LND和BC模型，其中BC模型RMSE值比其他3种模型RMSE值高一个数量级，BC模型对5种土壤类型模拟效果最差。综合比较拟合误差分析可知，VG和MG模型对黑土区土壤模拟精度最高。

表4 4种模型模拟土壤水分特征曲线R、RSME和残差平方和Table4 R,RSMEand sum of squared residualsof soil water characteristic curvecompared to simulationsfor four models

3 讨论

本研究利用4种土壤水分特征曲线经验模型拟合5种不同质地土壤曲线，4种模型拟合结果较佳，其中BC模型在拟合过程中低估土壤滞留含水率和土壤进气值，由于实测饱和含水率存在误差，导致出现低估土壤滞留含水率和土壤进气值现象。模型模拟结果中高吸力段拟合大于实测值，由于高速离心机测定过程中土壤结构被破坏，容重改变，导致误差[25]。

对比分析4种经验模型模拟结果可知，VG和MG模型模拟5种不同质地土壤效果最好。丁新原等比较VG和其他模型的土壤水分特征曲线模拟结果，VG模型模拟精度最高，与本研究结果一致[20,23,26]，因VG和MG模型中各参数均有明确物理意义[19,27]。Matlan等利用4种模型模拟分析黏土、砂土、粉土3种土壤质地，表明BC模型对实测值拟合效果最差，与本文研究结果一致[19]。其他4种土壤质地，BC模型对砂土模拟效果最优，表明BC模型更适合模拟粗质地土壤水分特征曲线[28]。