以形助阵 巧解高考离心率问题

刁金杰

东莞市电子科技学校 广东东莞 523710

离心率是圆锥曲线的一个重要性质，因此在高考中常以小题的形式出现。这类问题有着浓厚的几何特征，若能深入挖掘、巧妙利用，往往就能破解玄机。

例1【08江西理7】已知F1、F2是椭圆的两个焦点，满足的点M总在椭圆内部，则椭圆离心率的取值范围是（）

例2【07湖南理 9】设F1、F2分别是椭圆的左、右焦点，若在其右准线上存在使线段的中垂线过点，则椭圆离心率的取值范围是（ ）

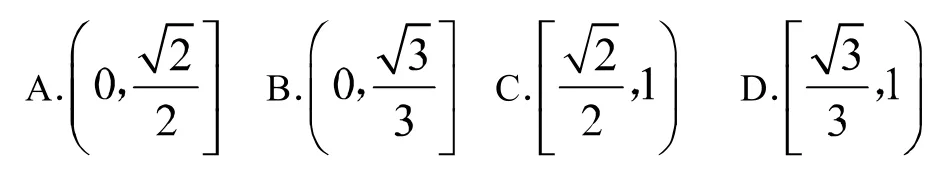
【评析】这是一道较难的选择题，学生不易从条件中发现不等关系，从而确定离心率的取值范围。关键语句“右准线上存在P使线段PF1的中垂线过点F2”。尝试着画图，图像告诉我们，问题可以转化为“以为F2圆心，焦距为半径画圆。当圆与右准线有交点时，交点P与F1的连线就是圆的一条弦，弦的中垂线必过圆心F2。”在深入挖掘其几何特征后，我们揭开了本题的神秘面纱，其本质是直线与圆的位置关系问题。所以，只需 。即

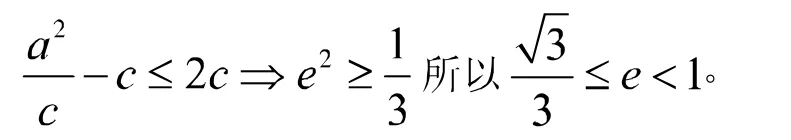
【评析】本题几何特征比较明显，作出图像后我们便可发现△OAP是等腰直角三角形，

例4【08全国Ⅰ理21】双曲线的中心为原点O，焦点在x轴上，两条渐近线分别为 ，经过右焦点F垂直于 的直线分别交 于A,B两点。已知成等差数列，且同向．（Ⅰ）求双曲线的离心率；

【评析】本题条件较多，最好先转化为图形语言。

于是，离心率的几何特征便显现了：

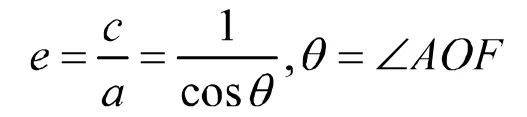
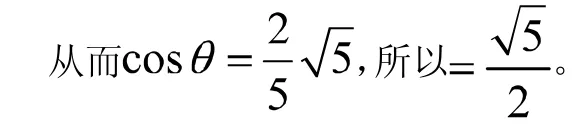
通过以上4例，我们可以看出重视几何特征对于解离心率问题常能起到事半功倍的效果。