微波检测器数据计算行程时间的方法

辛光照

（成都市规划设计研究院，成都 610041）

1 引言

在智能交通系统中，交通供给方在科学分配交通量、合理编制运营计划和统筹制定交通管理规划时，都需要行程时间等基础信息。在典型的“四阶段”交通需求预测模型中，交通分配需要基于行程时间等信息；在公共交通运营公司制定运营计划时，也需要行程时间以期获得最佳的运输效率。同样，交通需求者在进行路径选择和交通方式选择时，行程时间也是影响决策的主要因素。同时行程时间也是交通管理中评价道路服务水平的一项主要因素。总之行程时间在交通系统中，是影响交通供给者、需求者和管理者决策的主要因素[1]。

美国联邦公路局的BPR路阻函数[2]能够求解路段行程时间，但是由于路段上的自由流速度和实际通行能力因地而异，标定路阻参数需要大量实验，而且该函数不适合高饱和流量情况。为了完善BPR路阻函数计算路段行程时间的不足，王炜[3]应用大量的交通观测数据建立了各级公路在不同交通负荷条件下的车速—流量关系模型，提出了各级公路在不同设计车速下的实用模型参数，该模型适用于高峰小时超饱和状态下的行程时间估算。

张和生[4]利用出租车GPS数据研究了路段行程时间估算准确性，提出了大样本GPS数据采用样本均值、小样本量GPS数据利用顺序统计量方法估算路段行程时间的方法。曲鑫[5]根据浮动车数据估算行程时间存在5种类型的潜在误差，提出了修正浮动车数据估算行程时间的模型，通过模型有效性检验改善了利用低频浮动车估算路径行程时间精度不高的问题。付凤杰[6]研究了不同样本率下通过车牌识别匹配估算路段行程时间中位数的平均绝对百分比误差，提出了利用高清卡口数据估算行程时间的可行方法。

Baibing Li[7]根据感应线圈检测数据估算了在畅通、拥挤和混乱的三种交通状态下的车头时距，通过不同交通状态下的车头时距可以计算行程时间。在感应线圈检测数据的基础上，Ashish Bhaskar和Edward Chung[8]融合浮动车调查数据，对含有信号交叉口的路径行程时间进行了估算研究。Soriguera Marti[9]将感应线圈数据和收费站进出口统计数据融合，改进了高速公路行程时间估算和预测的方法，估算准确性相对单一数据源提升效果明显。Irum Sanaullah[10]利用车载GPS数据，提出了一种将车辆轨迹进行地图匹配高精度计算行程时间的方法。

近年来，国内一些大城市在城市快速路和主干道两侧安装了微波车辆检测器（RTMS），与观测数据、浮动车数据、感应线圈检测数据和GPS数据[11-16]不同，RTMS数据包含流量、平均速度和占有率等信息，通过对RTMS数据的挖掘分析，能建立一种计算路径行程时间的新方法。为保证路段行程时间计算结果的精度，需将路段划分为连续流路段和间断流路段。高速公路和城市快速路是连续流设施，通过在路侧设置RTMS检测器，以地点车速估计空间平均车速，可以得到路段行程时间。城市主干路路段行程时间会受到交叉口信号控制设施的影响，可将交叉口间的路段划分为连续流路段和间断流路段。连续流路段的路段行程时间与快速路相同，间断流路段的行程时间和交叉口处的延误进行统一计算。交叉口延误与信号配时、交通量、信号周期等因素有关，主要计算方法有英国的Webster延误公式和美国HCM延误模型。

根据RTMS数据的特点，为适应不同交通流在车道和道路纵向断面分布的特点，本文提出了3种基于RTMS数据的连续流路段行程时间计算方法；将间断流路段划分为交叉口影响路段和交叉口延误路段，两部分路段的行程时间组成了间断流路段行程时间；接着以北京清华东路—德胜门外大街为研究路径，采用C#语言编程，从原始检测器数据库中提取出每个车道的检测器数据，以30分钟为单位，分时段分车道分方法计算了研究路段的路段行程时间；然后通过交通调查研究路径沿途交叉口在早高峰、平峰和晚高峰的信号配时和车辆到达等数据，应用Webster延误模型计算了车辆平均延误，由车辆平均延误和路段行程时间得到路径行程时间；最后通过研究路径的调查行程时间和仿真行程时间，对计算行程时间的准确性进行了分析。

2 路径行程时间计算方法

2.1 连续流路段行程时间

根据RTMS数据的特点，考虑不同道路的流量在车道和道路纵向断面的空间分布特征，提出了3种连续流路段行程时间计算方法。第一种是基于车道划分的路段行程时间计算方法（方法1），这是后面方法的基础，适用于研究不同车道的行程时间。第二种方法考虑了流量在车道上分布不均匀的情况，引入车道权重因子，建立了基于车道流量分布的路段行程时间计算方法（方法2），适用于研究流量在不同车道分布不均衡条件下某行车方向的行程时间。第三种模型在第二种基于车道流量分布的路段行程时间估计模型的基础上，引入检测点权重因子，建立了改进的基于车道流量分布的行程时间计算方法（方法3），适用于研究流量在不同车道和道路纵向断面分布不均衡条件下某行车方向的行程时间。

2.1.1 基于车道划分的路段行程时间

方法1中连续流路段i的j车道行程时间的计算公式为：

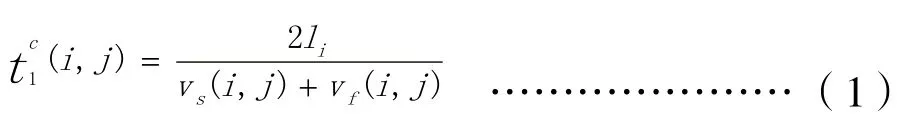
式中，vs(i, j) 和vf(i, j)表示路段i的j车道的起点和终点平均车速；li表示路段i的长度；t1c(i, j)表示路段i的j车道的行程时间。

j车道路段（共划分为n个路段）总的行程时间表示为：

2.1.2 基于车道流量分布的路段行程时间

方法2以检测点处的车道流量为基础，引入车道权重因子，计算m个车道平均车速的加权平均值，得出路段i起点的车速为：

式中，aj是j车道权重因子，满足

方法2中连续流路段i行程时间是：

连续流路段总的行程时间表示为：

2.1.3 改进的基于车道流量分布的路段行程时间

方法3在车道权重因子的基础上，以路段起点和终点检测的交通量作为路段起点和终点影响权重，计算路段行程时间，方法3的算法表达式是：

式中，h表示路段起点权重因子，其他符号意义与上面相同。

2.2 间断流路段行程时间

车辆行驶至交叉口进口道附近时，遇到红灯会减速停车等待。以车辆开始减速的路段位置为起点，到交叉口停车线为终点作为交叉口延误路段。交叉口延误路段起点至交叉口上游RTMS的路段位置作为交叉口影响路段。车辆在交叉口延误路段的行程时间通过调查车辆到达交叉口的规律、交叉口控制和设计因素，应用Webster延误模型计算。交叉口影响路段的行程时间结合交叉口上游RTMS检测到的交通流运行参数进行估算。交叉口延误路段和影响路段两部分行程时间之和等于间断流路段行程时间。

Webster延误模型的计算公式是：

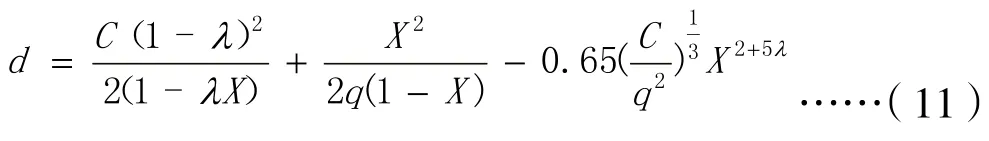
式中，d是每辆车的平均延误；C是信号周期；λ是绿信比；q是到达交通量；X是饱和度（流量/通行能力）。

2.3 路径行程时间

路径行程时间是连续流路段间、交叉口影响路段和交叉口延误路段的行程时间总和。

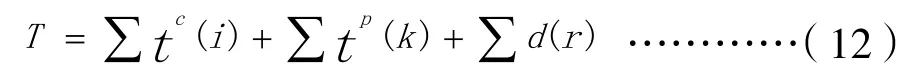
式中，tc(i)是第i个连续流路段的行程时间；tp(k)是第k个交叉口影响路段的行程时间；d(r)是第r个交叉口延误路段的行程时间。

3 实例行程路径

研究路径是清华东路—德胜门外大街，由主干路和快速路组成，起点是清华东路北京林业大学站，途经北沙滩桥、安翔桥、健翔桥、健德桥、马甸桥，终点是德胜门进口处。路径全长8.11公里，共有18个检测器，图1是研究路径，图中标记代码是微波检测器编号，以两检测器之间的路线为路段单元，划分为17个路段单元。

清华东路沿线共有3处信号控制交叉口，从东向西依次是清华东路与志新西路信号交叉口、清华东路与学院路信号交叉口、北京林业大学处信号交叉口，信号交叉口位置分布如图2所示。三处交叉口分别位于检测器01-02，02-03和04-05间，以信号交叉口01-02、02-03和04-05分别代表三处交叉口。

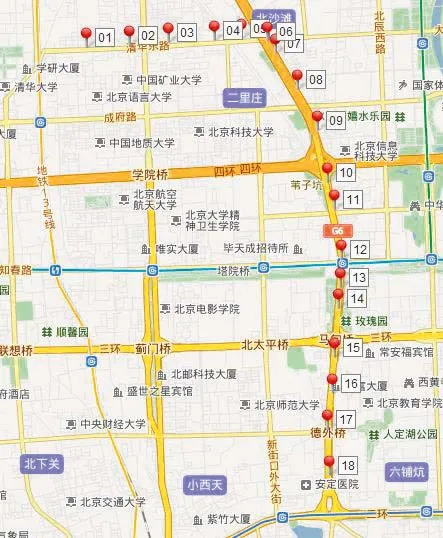
图1 研究路径

图2 信号交叉口位置分布

3.1 连续流路段行程时间计算

3.1.1 方法1：基于车道划分的行程时间

微波检测器提供的原始数据是6车道的数据，在计算前需要分离出每个车道的检测数据。利用C#语言编程可以根据检测器的原始数据提取出每个车道的检测数据。根据上步提取的每个车道的数据，选取07:20-07:50作为早高峰时间段，13:30-14:00作为平峰时间段，17:30-18:00作为晚高峰时间段，顺着研究行车方向的3车道共选取了162个检测数据文件。利用C#语言编程计算出每个车道的各个检测点在早高峰、平峰和晚高峰三个时间段的平均地点车速，以两个检测器之间的路段作为路段单元，路段两端的检测器编号作为路段标号，将每个车道两个相邻检测点的地点车速平均值作为两检测点间路段的平均行程车速，得到各个路段的不同车道在早高峰、平峰和晚高峰时间段的平均行程车速。根据路段距离和路段间每个车道的平均行程车速计算出每个路段的不同车道在早高峰、平峰和晚高峰时间段的平均行程时间。以早高峰时间段为例，基于车道划分的早高峰路段行程时间的计算结果见表1。

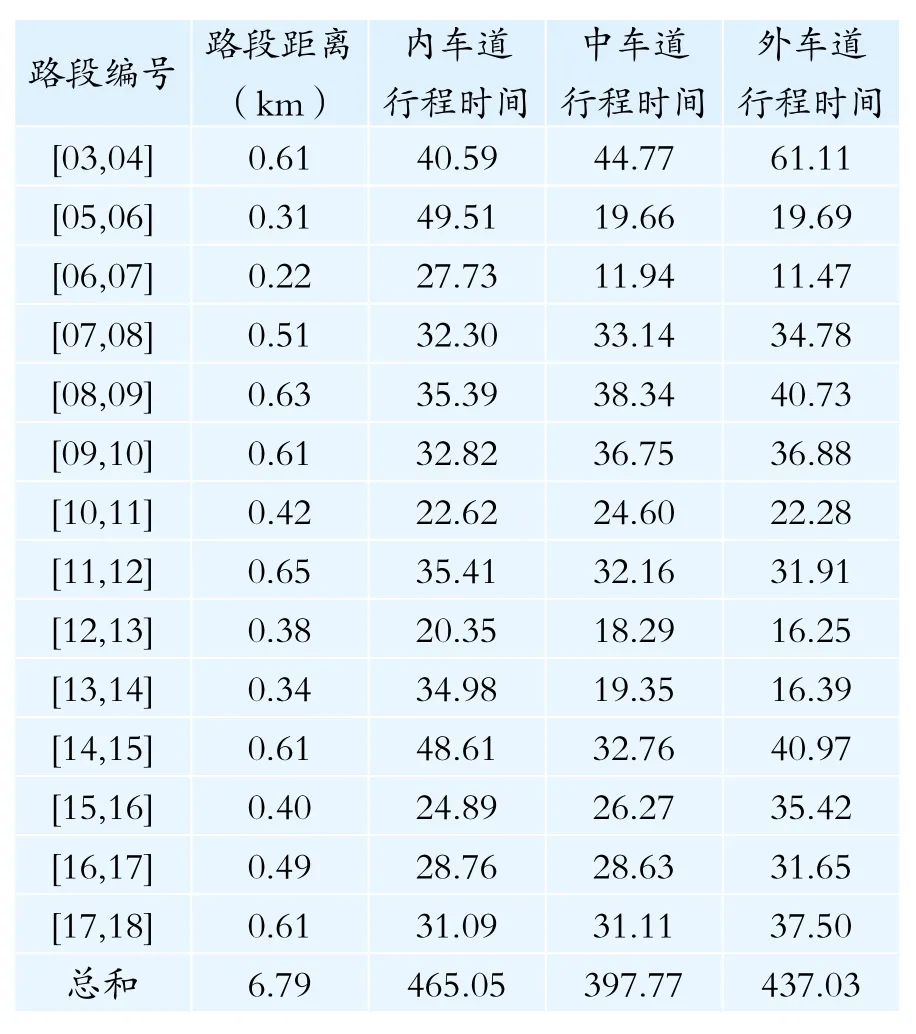
表1 基于车道划分的早高峰路段行程时间（秒）

3.1.2 方法2：基于车道流量分布的行程时间

在实际的车辆行驶中，驾驶员一般不会固定在某一车道行驶，根据车头间距和速度状况会变换行车道，具有一定的灵活性和随机性。方法1适用于车道流量分布不均匀条件下不同车道的交通流参数对比。一般情况下交通参与者关心的行程时间并没有局限在车道行程时间上，一般是指某一行车方向的行程时间，因此进一步提出了基于车道流量分布的行程时间估算方法。在计算某一行车方向的行程时间时，以车道行程时间为基础，考虑流量在各车道上的分布，以检测点各车道交通量为影响权重，计算各车道行程时间的加权平均值，在此基础上计算该行车方向的行程时间。以早高峰为例的车道权重因子的计算结果见表2。

表2 早高峰时间段各车道权重因子

3.1.3 方法3：改进的基于车道流量分布的行程时间

方法2考虑了流量在车道上分布不均衡的情况，能估算流量在不同车道分布不均匀条件下的某一行车方向的行程时间。针对沿道路纵断面流量分布不均匀的情况，在方法2的基础上，以路段两端的检测交通量作为检测点权重因子，计算路段两端检测点的地点车速的加权平均值，即改进后的路段平均车速（表3），然后根据路段长度计算路段行程时间。

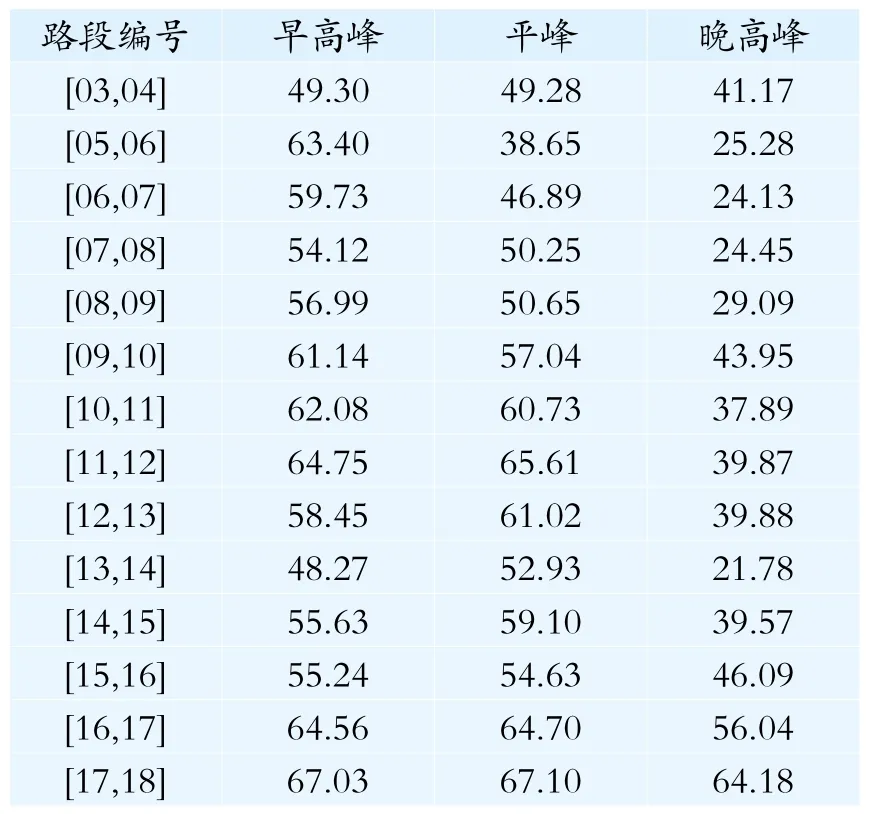
表3 改进后的路段平均车速（千米/时）

3.2 间断流路段行程时间计算

受信号交叉口影响，路段[01,02]、[02,03]和[04,05]属于间断流路段。计算间断流路段的行程时间包含交叉口延误路段的延误和交叉口影响路段的行程时间。通过实地交通调查，获取信号交叉口01-02、02-03和04-05处早高峰、平峰和晚高峰时间段内东西直行方向的基础数据（表4），应用Webster交叉口延误模型公式计算出各个时间段内的交叉口平均延误。

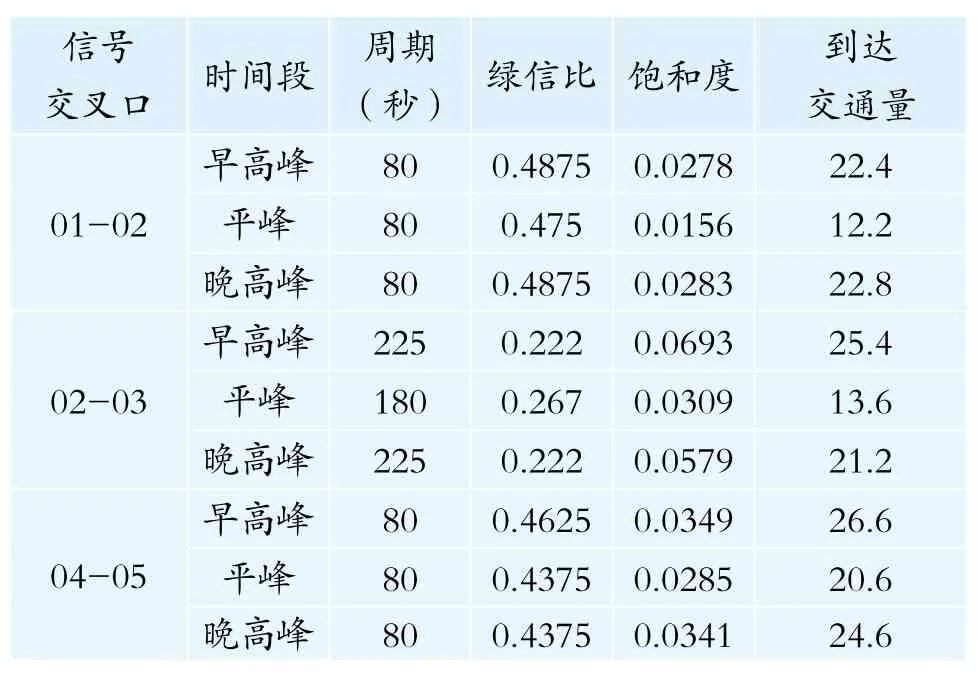
表4 信号交叉口01-02、02-03和04-05调查数据

综合交叉口延误路段的延误和交叉口影响路段的行程时间，得到间断流路段早高峰、平峰和晚高峰时间段内的行程时间见表5。

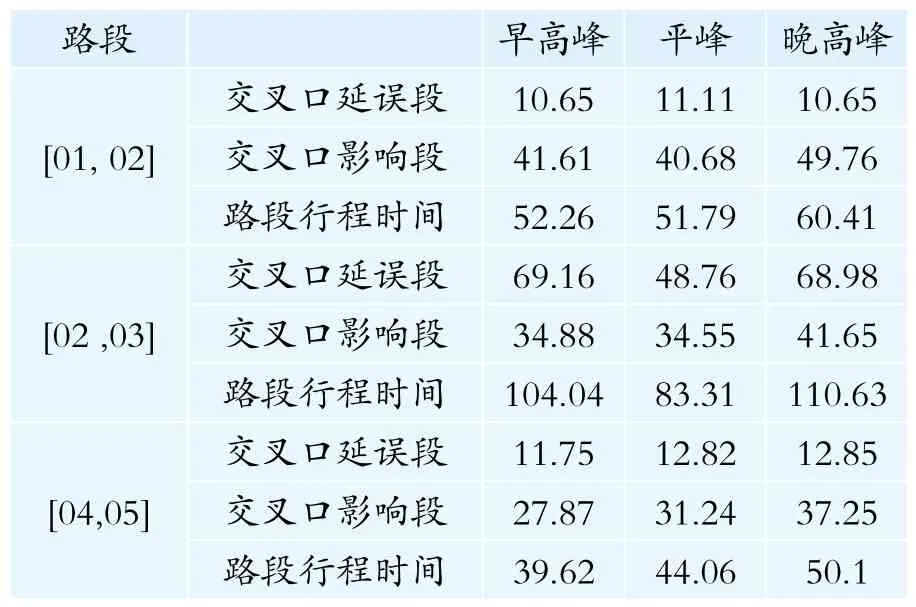
表5 间断流路段行程时间计算结果（秒）

3.3 路径行程时间计算结果分析

研究路径的行程时间等于连续流和间断流路段行程时间之和。沿清华东路至京藏高速路方向，从北京林业大学南门到德胜门的各研究时段内的行程时间见表6。

表6 研究路径在三种行程时间计算方法中的行程时间（秒）

通过分析三种计算方法的结果（图3）可以看出，方法1基于车道划分的行程时间中不同车道的行程时间存在一定的差异，这反映了流量在研究路径的横断面车道上分布不均匀。方法1中间车道的行程时间最接近方法2基于车道流量分布的计算行程时间，这反映了车辆在研究路径的横断面中间车道上分布最多。方法2基于车道流量分布的计算行程时间和方法3改进后的基于车道流量分布的计算行程时间相差不大，这反映了流量在研究路径的纵向断面上分布均匀。

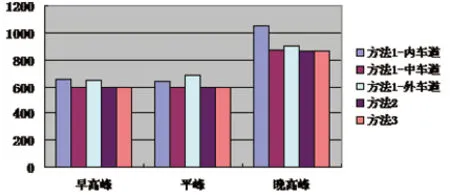
图3 行程时间计算结果对比（秒）

在早晚高峰和平峰时间段内借助跟车法，沿着研究路径进行实地交通调查。实地跟车调查结果表明，在早晚高峰时间段内路段调查行程时间与方法2基于车道流量分布的计算行程时间和方法3改进后的基于车道流量分布的计算行程时间相差不大；在平峰时间段内，路段调查行程时间与方法1中间车道的计算行程时间最接近。为了进一步验证本文提出方法的有效性，在路段调查行程时间基础上，通过VISSIM交通仿真软件建立研究路线的仿真模型获取路段仿真行程时间。以早高峰时间段为例，调查和仿真路段行程时间与方法3改进的基于车道流量分布的计算行程时间的对比如图4所示。路段调查行程时间与路段计算行程时间的平均绝对百分比误差（MAP1）的平均值为9.33%，其中最大值和最小值分别为15.58%和3.54%。路段仿真行程时间与路段计算行程时间的平均绝对百分比误差（MAP2）的平均值为4.15%，其中最大值和最小值分别为9.87%和1.41%。

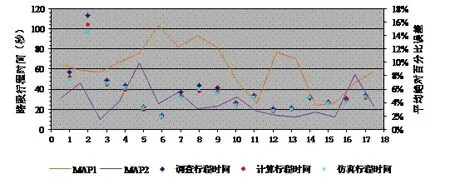
图4 各路段行程时间的调查、计算与仿真结果对比（秒）

4 结论

微波车辆检测器提供的交通流检测数据能够应用于行程时间估算新方法的研究。本文提出的第1种基于车道划分的行程时间计算方法能够分车道进行行程时间估算。第2种基于车道流量的行程时间计算方法能够估算流量在道路横断面不同车道分布不均匀条件下特定行车方向的行程时间。针对流量在道路横断面不同车道和纵断面不同路段分布不均匀的情况，提出了第3种改进的基于车道流量分布的行程时间计算方法。3种行程时间计算方法涵盖了交通流空间分布的不同特征，能用于计算不同交通流条件下的行程时间。