移动云中基于随机博弈的多用户任务卸载效用优化

张锋辉，符茂胜，刘伟荣

(1.皖西学院 电子与信息工程学院，安徽 六安 237012；2.中南大学 信息科学与工程学院，长沙 410083)

0 引 言

随着移动互联网的蓬勃发展，移动终端设备由于其便携性得到了越来越广泛的应用，一份2016年中国互联网发展状况统计报告显示，中国大陆地区使用手机上网的网民比例为90.1%，且呈逐年增加趋势[1]。但不断复杂的移动应用程序如人脸识别、增强现实等给移动设备带来了巨大负担。移动云计算技术允许将设备的计算任务卸载到云计算服务器上执行，极大缩短了移动应用程序执行时间且降低设备电能损耗，因此移动云计算这种巨大优势得到了业内越来越广泛的关注[2-4]。

在移动云计算中设备可以将任务卸载至远程云、本地微云或由附近设备组成的移动云，而卸载任务至移动云能够较大程度地降低任务传输时间、减少无线带宽使用及降低云计算费用,因此利用移动云进行计算的方式得到国内外众多学者的深入研究[5-6]。但不合理的任务卸载会导致任务执行时间变长、费用增高等问题，特别是当移动云中多个资源需求节点(resource demander,RD)同时向资源提供节点(resource provider,RP)卸载任务时，无序的任务卸载策略会极大地降低移动云计算效率。因此，合理的任务卸载策略是提高移动云服务效率的关键。

鉴于此，本文对移动云中多个RDs同时向RPs卸载任务的情景进行研究，针对降低各个RD卸载任务的执行时间问题，提出了基于随机博弈的任务卸载策略。文中以移动云每个RD卸载任务至RPs所节省的时间为各自效用，建立基于RDs效用最大的优化模型。按照任务完成的时间将云计算卸载分为多个时间片，并利用任务产生的特点将节点效用优化问题转化为各个RD为使自身的效用最大化而进行任务卸载博弈问题。建立随机博弈模型并针对该模型提出了反向迭代算法得到博弈的纳什均衡策略，实验将该策略与静态博弈获得的策略进行对比，结果表明,采用随机博弈方法获得的策略能够明显提高每个RD的效用，从而提高移动云的计算效率。

1 相关工作

近年来,针对移动云中通过任务卸载而提高RD的效用问题，国内外学者分别从时间、能耗等方面进行了大量研究。针对在异构网络下移动云节点的任务分配问题，Lu等[7]提出离线集中式方法和在线分布式方法优化了任务执行时间。Zhang等[8]针对中断容忍网络下移动云工作量分配问题提出分布式算法减少任务执行时间。Yaqoob等[9]针对降低移动云中任务执行时间和能耗问题提出异质性感知的任务分配算法。Shi等[10]在固定任务执行时间和能量消耗限制条件下提出了基于高能量效率的移动云任务调度算法。Zhang等[11]使用了分布式算法进行任务卸载，提高移动云各个节点的效用。这些研究从不同角度优化了移动云节点的任务分配，从而减少任务执行时间或降低能耗，但这些研究仅针对处理单个节点任务卸载的优化问题，没有考虑到多个节点任务卸载时的竞争关系。

当移动云中有多个节点进行任务卸载时，Tang等[12]提出了双侧竞价机制提高了移动云中RDs和RPs的效用。Kim等[13]针对合作环境和非合作环境下的移动云，引入李雅普诺夫飘移惩罚因子进行双侧控制，降低RDs和RPs的成本，提高移动云计算效率。但这些研究主要考虑的是有代理进行移动端管理的场景，没有考虑多个RDs根据自身的情况直接将任务卸载到RPs的情景，因此,本文针对此情况进行研究，提出了基于随机博弈的RD任务卸载策略，提高了移动云任务执行效率。

2 系统模型

移动云中的节点主要由资源需求节点RD和资源提供节点RP组成，它们通过ad-hoc网络进行连接，任意设备之间的通信距离为1跳。该系统中RD的数量为N，RP的数量为M，且RD可同时卸载多个任务到不同的RP。由于计算任务会不断产生，本文将任务卸载过程划分为多个时间片进行研究，并将每个时间片定义为任意RP节点完成任务所需的最长时间。当计算任务产生后会自动进入队列等待卸载[14]，设第i个RD队列的长度为Li。该移动云系统如图1所示。

在每个时间片中会有数量不等的任务产生，设在时间片t内有ai个任务产生并到达队列，且到达队列的任务数量呈泊松分布[15]。每个任务具有不同的数据量，其中，任务的数据量服从均值为zi的独立同分布。每个任务的数据处理密度使用γ(cycle/bit)表示，数据处理密度指处理单位数据所需CPU周期，且每个RD的数据处理密度服从均值为γi的独立同分布[16]。数据量的最大值为zmax，计算密度的最大值为γmax，可知0≤zi≤zmax,0≤γi≤γmax。在该移动云中第i个RD的CPU处理速度为pi(cycle/s)，处理每个任务的平均时间为

(1)

图1 移动云中任务卸载示意图Fig.1 Task offloading in mobile cloud

在时间片t内RD取出di个任务进行卸载，同时有ai个任务到达队列，此时队列中的任务数量为si，如果任务可全部进入队列，则在下一个时间片中队列的任务数量为

(2)

该移动云中网络传输速率为v(bit/s)，在任务传输过程中由于RD卸载的数据量远小于接收结果的数据量，因此,在传输过程中所需时间可仅考虑任务卸载的时间[17]，故任务在传输过程中所需的平均时间hi=zi/v。 在移动云资源提供方RP中，使用cj(cycle/s)表示第j个RP的CPU处理速度，当任务量为G时，第j个RP处理该任务所需时间为G/cj[18]。在每个时间片中，第i个RD从队列中取出一定数量的任务进行卸载，任务数量使用di表示，且RD将这些任务分配到不同的RP上，设分配给第j个RP的工作量为bij，第j个RP完成所有工作所需的时间为

(3)

(4)

将每个RD进行任务卸载所节省的总时间定义为其效用，因此,第i个RD卸载任务所获效用ui=twi-dihi。在移动云中，每个RD通过任务卸载获取自身最大化效用，可得到的公式为

maxui

(5)

s.t. 0≤zi≤zmax

0≤γi≤γmax

0≤di≤Li

3 随机博弈建模

由于每个时间片中RD任务产生具有随机特性[13]，根据(5)式无法确定每个RD卸载任务的数量，不能确定其最优的收益，而在多个时间片内研究任务卸载，采用随机博弈的方法可确定每个RD的最优卸载策略。因此，本文将每个RD的效用优化问题转化为RD为获得最大效用而进行博弈的问题。在该系统中每个RD是一个玩家，则该博弈为N玩家随机博弈。在每个时间片中，第i个RD首先取出di个任务，并将其卸载到不同的RP，同时新产生任务到达队列，如果任务的数量超过第i个RD中队列的容量，RD需自行处理多余的任务。因此，在动作di条件下第i个RD的队列中任务数量的转移概率为

(6)

(7)

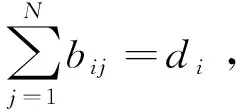
(8)

P(S′|Si,(bi1,…,diM),(b-i1,…,b-iM))=

(9)

(9)式中，(b-i1,…,b-iM)表示不包含第i个RD的其他所有RD的动作。 当其他RD的动作固定时，第i个RD在每个状态下的策略可通过(10)式获得。

(10)

4 反向迭代算法

在随机博弈中需要确定每个状态下各个RD的最优动作，本文提出反向迭代算法进行计算。首先假设除第i个RD外其他RD的最优动作为(b-i1,…,b-iM)*，然后使用(11)式计算出在该条件下第i个RD的最优策略。

(11)

利用(11)式得到第i个RD的动作，并根据(12)式计算其收益。

(12)

在每次迭代过程中根据(11)—(12)式进行计算，直到前后2次长期收益的差值小于ε，此时该博弈已经达到ε-纳什均衡[6]。其迭代过程如图2所示。

图2中首先初始化每个RD的值及第1到第N-1个RD所有状态下的策略，并根据其他RD的策略得到第N个RD的最优策略，而后根据第N个RD和第1到第N-2个RD的策略得到第N-1个RD的最优策略，最终得到所有人的最优策略。根据所有RD的最优策略和初始值得到RD所有状态下的值，自此完成1次迭代。根据上次迭代得到每个RD的策略进行第2次迭代，直到所得的值和上次迭代的值相减小于ε时停止迭代，此时该博弈达到ε-纳什均衡，各个RD在每个状态下得到的策略为最优策略。

5 实验仿真

本节首先验证该博弈的收敛性，并比较不同参数时系统特性，其次将随机博弈的方法和静态博弈的方法进行对比。该系统中所有节点随机散布于一个圆形空间，该空间中有3个RD和5个RP[13]。所有RD和RP均是现有常见的移动端，其CPU处理频率为[1,2]GHz，数据量大小zi为[0.15,0.25]Mbit，计算密度γi为[2,5](Kcycle/bit)，每个RD的队列可以存储5个任务即Li=5，网络传输速率为5 MHz[19]。实验中RD和RP的所有参数分别如表1和表2所示。

表1 RD的参数设置Tab.1 Parameter setting of RDs

表2 RP的参数设置Tab.2 Parameter setting of RPs

设置迭代停止条件ε=0.001，比较折扣系数对收敛性的影响，当β=0.9，β=0.8，β=0.7时，从图3中可以看出该随机博弈是收敛的，当折扣系数越小算法的收敛速度越快，当β=0.7时该系统经迭代14次便可收敛。

同样，当每个RD中队列容量不同时其获得效用也不同，图4显示了不同队列容量的RD效用，可以看出当队列容量较大时RD效用也较高，这是由于队列容量大时，每个RD可以卸载的任务量具有更多的选择性。

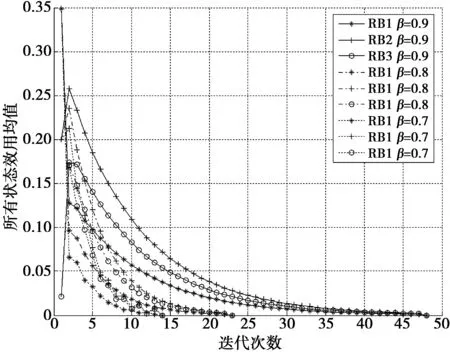
图3 随机博弈的收敛性Fig.3 Convergence of stochastic game

图4 不同队列容量时RD效用比较Fig.4 Comparison of RDs’ revenue with different queue capacity

为了与随机博弈获得的策略进行对比，本文设计静态博弈的方法，即在每个时间片内RD执行相同的策略，如把队列中所有的任务全部卸载，而后进行分配博弈。实验在10个时间片中对比了这2种方法，图5显示不同RD在每个时间片上的收益。从图5中可以看出，采用随机博弈的方法，每个时间片上RD的收益波动不大，这是因为当任务随机到达时，采用随机博弈的方法RD会考虑到当前和以后时间片任务到达概率对长期收益的影响而做出决策，因此收益波动不大，且在大多数时间片中采用随机博弈方法获取的效用明显高于采用静态博弈的效用。

图6显示了采用随机博弈和静态博弈方法下每个时间片中所有RD总效用的对比。从图6中可以看出，采用随机博弈下所有RD的总效用明显高于采用静态博弈的总效用，这是因为采用随机博弈时每个RD会根据自身和其他RD的状态采取卸载动作，避免了当所有RD都进行卸载而造成效用下降问题。图7显示了10个时间片中每个RD的总效用，可以看出采用随机博弈的方法每个RD可获得更高的效用。

图5 不同时间片采用随机博弈和静态博弈RD效用的对比Fig.5 Comparison of RDs’ revenue with stochastic game and static game in different time slots

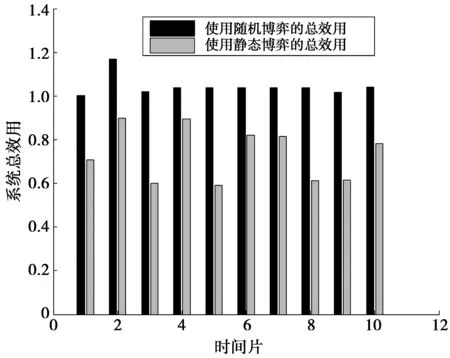
图6 采用随机博弈和静态博弈RD效用和的对比Fig.6 Comparison of total revenue for all the RDs between stochastic game and static game

由于每个RD的效用是任务卸载所节省的时间，因此，采用随机博弈获得的策略缩短了任务执行时间，提高了移动云的服务效率。当移动云的节点固定时，每个RD只需要运行一次反向迭代算法便可获得节点的最优卸载策略，且当折扣系数小于0.7时，算法所需的迭代次数会低于10次，其运行时间也会更少。

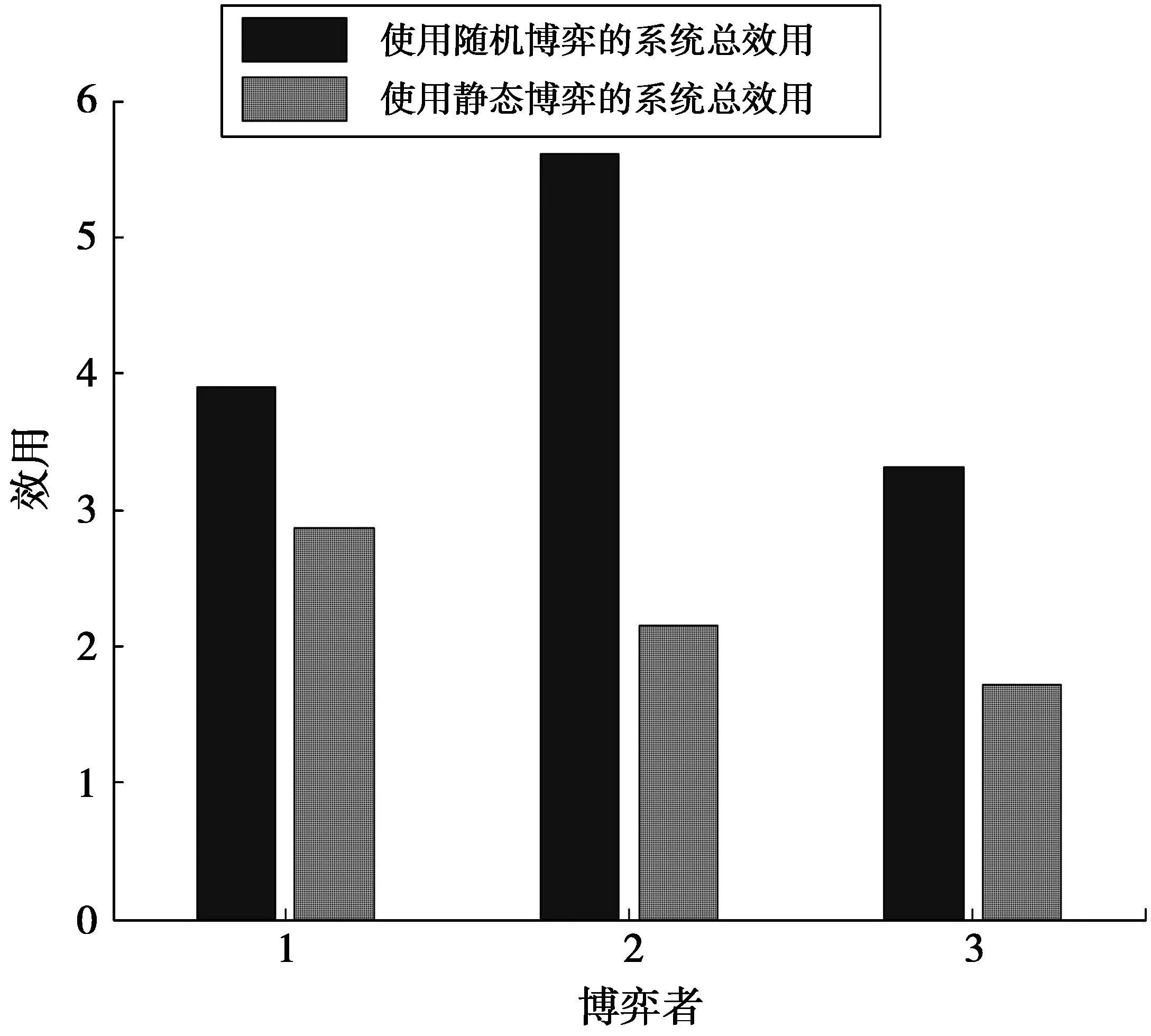
图7 采用随机博弈和静态博弈每个RD总收益的对比Fig.7 Comparison of total income per RD using stochastic game and static game

6 结 论

文中针对任务随机到达情况下，移动云中多用户任务卸载的情景进行了研究。以各个RD进行任务卸载所节省的时间为其效用，建立优化模型，并根据任务随机到达特性将其转化为多用户随机博弈模型，提出反向迭代算法得到ε-纳什均衡。最后和静态博弈策略进行了仿真对比，结果表明，使用随机博弈获得的策略使每个时间片内RD效用更加稳定，同时降低任务运行时间、提高移动云服务效率。