从奥苏贝尔认知同化理论谈高等数学教学

闫婷婷

奥苏贝尔认知同化理论始创于20世纪60年代，是诸多现代教育理论中最重要的理论之一.奥苏贝尔的先行组织者策略：在教学准备阶段，教师要设计一个引导性材料称为先行组织者，这个引导性材料能够在学生们的新旧知识之间起衔接作用，帮助学生用认知结构中已有的观念去同化新知识面［1-2］.奥苏贝尔主张学生的学习必须有意义，同时也给出类属学习、总括学习、并列学习三种有意义的学习策略.类属学习是把新观念归入认知结构中原有观念的适当部分并使之相互联系，在类属学习中原有观念是总观念，新观念是从属观念；总括学习是在若干已有的从属观念基础上归纳出一个总观念，总括学习所形成的新观念在概括和包摄程度上高于原观念；并列学习是指新观念与认知结构中原有观念既不从属也非总括，只是和原有认知结构中的整体内容有一般关系［3-4］.奥苏贝尔的课堂教学观是：主张教师用语言讲授的方式进行教学，同时反对教师滔滔不绝地讲学生静静地听式的教学，倡导师生在教学中相互作用.

高等数学其概念的高度抽象性和方法的极端灵活性使其难以被学习和掌握.本文利用奥苏贝尔先行组织者策略和有意义学习理论克服上述困难，在教学实践中取得理想效果.

1 高等数学的先行组织者策略

针对高等数学教学中经常遇到的困难与问题，笔者总结出三种先行组织者策略.

1.1 动画演示式先行组织者策略

动画演示是理解高度抽象概念的有意义手段，它能将概念中的运动和变化淋漓尽致地展示其中，给人一目了然的感觉，帮助学生从直观走向抽象.动画演示作为先行组织者可用于一些疑难概念的讲授，如数列极限定义、函数极限定义、导数定义、定积分与二重积分定义等.例如，在讲授右极限的定义之前，制作动画如图1所示.讲授时将其先向学生呈现.

图1 右极限动态图

从图1可以看出，当自变量x从a右侧无限靠近a时，圆中动点p沿曲线无限靠近Q点，进而拉动函数y无限趋近于A.动画直观地揭示了右极限的真实含义，据此，教师可轻松地引导学生给出右极限的描述性定义.这里，动画演示作为先行组织者起到了将旧知识函数几何图形与新知识右极限联系起来的作用.

1.2 函数图形式先行组织者策略

高等数学中的许多定理与性质都有直观的几何背景.因此，可以将几何图形作为一些定理与性质的先行组织者，如局部有界性定理、拉格朗日中值定理、单调性判别法、曲线凹凸性判别法等.

例如，在讲授曲线凹凸性判别法之前，先向学生呈现图2所示的上凸图形，教师引导学生发现切线的斜率（f′()x）随自变量x的增大而逐渐减小⇒f″(x)＜0，进而引出上凸判别法.这里，函数图形作为先行组织者起到了联系旧知识二阶导数与新知识上凸判别法的作用.

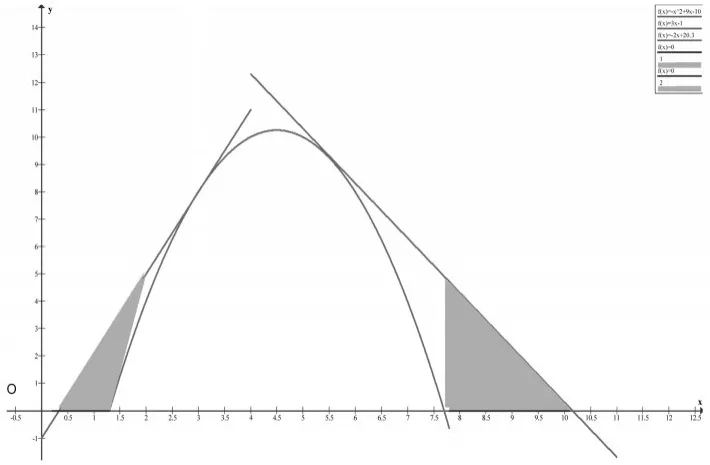
图2 切线与上凸曲线图

1.3 问题情境式先行组织者策略

好奇是人的本性，而问题恰是刺激个体产生好奇的重要因素.教师可依据新知识的内容创设问题情境把学生带入新知识的讲授，学生会因为好奇而关注新旧知识的联接.问题情境式先行组织者是高等数学教学中最常用最方便的形式，几乎每个章节都可采用.

例如，在讲授洛比达法则之前先向学生呈现一个具体的0/0型未定式，学生会因旧知识不能解决问题而产生困惑，而困惑会激发学生寻求新知识的心里冲动.此处，具体的0/0型未定式作为先行组织者起到了旧知识导数与新知识洛比达法则相联系的作用.

除具体问题之外，还可以设计比较抽象的问题情境式先行组织者.例如，问题：已知v(t)，如何求s(t)作为不定积分的先行组织者；问题：如何求无穷多个数的和作为常数级数的先行组织者；问题：如何用一些简单函数逼近一个复杂函数作为幂级数的先行组织者等.

2 高等数学的有意义教学策略

与学生的有意义学习相对应的是教师的有意义教学，所谓有意义教学是指教师的教催生了学生有意义的学.因此，实施有意义教学的原则是：采用行之有效的方法，促进学生将旧知识与新知识发生作用，用旧知识理解新知识而产生同化，并把同化后的新知识纳入到已有认知结构建构成新的认知结构.根据奥苏贝尔有意义学习的三种方式，可派生出三种有意义的教学策略.

2.1 类属教学策略

类属教学策略与类属学习方式相对应.类属教学的过程是：教师依照学生认知结构中最清楚最牢固的若干知识点（如a、b、c）将新知识A分解成几个简单的小项，每个小项都容易从上述知识点（a、b、c）得到理解，在逐项讲解之后再综合回到新知识A，这是一个化繁为简、化难为易的过程.

例如，分部积分法作为新知识，初学者很难分清u和v，也不知分部积分公式如何使用.如果把分部积分法分解成：何时使用分部积分法、如何理解分部积分公式，使用公式的经验技巧三个小项，每个小项学生都有旧知识去理解，最后将三部分综合贯通成分部积分法会产生理想效果.

类属教学策略常用于命题（定理、性质、法则、公式）的教学.在命题教学中，除了注重教学方式外，教师还需指导学生用命题的证明认知命题的内涵，用命题的应用认知命题的外延.因为命题的证明过程恰是旧知识同化新知识的过程，新旧知识之间的逻辑关系尽显其中；而命题的应用又是积累思路、方法、技巧的过程.

2.2 总括教学策略

总括教学策略与总括学习方式相对应.总括教学的过程是：通过诸多具体事例（如a、b、c等）某种表象进行判别比较，引导学生归纳出它们共有的标志性特征A，而且A这种标志性特征还具有广泛的意义，有必要给它起个名字深入研究，于是将其用数学语言抽象后有关A的新观念产生了.

事实上，人类对客观世界的认识大多采用这种方式.在高等数学中，微分（导数、偏导数）积分（定积分、重积分、曲线曲面积分）等概念均是这种方式的产物，总括教学策略自然能用于其中.除此之外，教师可以根据新知识的内容人为地设计几个具体实例，通过找出它们共同的标志性特征引出新知识.例如讲授数列{an}收敛于a的定义时，先向学生呈现几个具体的数列，从中分析归纳出它们共同标志性特征是：当n无限增大时，an与a的距离无限小，然后用n≥N刻画n充分大，用 |an-a|＜ε刻画an与a距离任意小，给出数列收敛于a的形式化定义.

2.3 组合教学策略

组合教学策略与并列学习方式相对应.组合教学的过程是：在讲授新知识A时，A与旧知识B既不是类属关系也不是总括关系，但A与B有一个共同的特征C.这样，教师在完成A的讲述后，将A与B组合起来再认知C.

例如，在讲授新知识拉格朗日中值定理时，它有证明代数不等式的功能，但旧知识函数的单调性也有证明代数不等式的功能，把两者结合起来，就有了两种证明代数不等式的方法.而在以后的新知识—曲线的凹凸性和马克劳林公式也有证明代数不等式的功能，再将它们组合起来，就有四种证明代数不等式的方法.

事实上，数学方法也是高等数学内容的一部分.学生学习高等数学的目的是应用，但有时求解某个问题所需的知识明明知道但问题却不会解决，究其原因多数是方法在作祟.因此，教师要充分利用组合教学方式，按问题目标指导学生积累教学方法.

3 案例——分部积分法教学设计思路

学生学习分部积分法的困难在于如何使用分部积分公式，其中怎样区别公式中的u和v更是难中之难［5-7］.用什么办法化难为易呢？表1是笔者综合使用问题情境先行组织者策略和类属教学策略讲授分部积分法的思路重点强调怎样用“三步法”化难为易的过程.

从表1可以看出，此教学设计5次使用了问题情境式先行组织者，通过不断设问不断解决使学生轻松地逐步接近分部积分法.“三步法”把区分u与v的困难转移到凑微分上，而凑微分是学过第一换元法的学生已经熟知的.口诀“d前d后两相乘，交换位置作积分”起到记忆公式的作用，为使教师的讲授与学生思维产生共鸣，本案例全程采用黑板加粉笔的讲授形式.

4 结论

由于先行组织者是先于新知识呈现之前展示给学生的连结新旧知识的引导性材料，所以先行组织者在教学中不可或缺.倘若缺失，学生会因思维的跳跃或间断产生困惑，进而产生排斥和畏惧心理.相反，如果善用先行组织者在新旧知识之间巧搭便桥，学生就会轻松愉悦地从旧知识走向新知识.

表1 分部积分法讲授思路表

学生学习高等数学必须是有意义学习而非机械学习，学生仅记住某些数学公式和概念而未理解毫无意义.理解是有意义学习的主要心理活动，为此，教师必须进行有意义教学.数学的知识与知识之间的包摄关系、归属关系、并列关系比比皆是，教师必须在充分理解教材的基础上，有目的地利用类属教学策略、总括教学策略、并列教学策略对教材进行加工处理，让其变成既刺激学生兴趣又易理解消化的材料，此处正是张扬教师个人魅力的地方.

高等数学具有高度抽象逻辑严谨的属性，新知识的思想方法和逻辑关系往往体现在教师板书的字里行间和抑扬顿挫的语言中.教师的表述和学生的思维产生共鸣而促进理解，这种刺激——反映的过程符合学生的认知能力和心理特征.因此，黑板加粉笔的教学形式仍然具有重要意义（如案例）.同时，笔者主张充分利用多媒体技术把蕴含于概念之中的运动和变化直观地呈现在白板（屏幕）上，思维靠黑板，直觉靠白板，黑白结合是高等数学教学的极佳方式.