随机共振基本理论介绍

刘廷银 刘岩 赵双江 中国人民解放军65589部队

1 引言

随机共振理论已经经历了数十年的发展，其研究深度和影响范围都极为深远。通常认为随机共振系统需要有三个要素：随机共振的输入驱动信号、非线性的随机共振系统和相匹配的噪声。随机共振按照稳态数量不同，可分为单稳态随机共振、双稳态随机共振，以及多稳态随机共振。其中研究较为成熟的是单稳态随机共振和双稳态随机共振，而双稳态随机共振与通信信号中的0,1二值可以较好地适配，因此得到了更为广泛的应用。因为多稳态系统的研究难度较大，所以应用较为有限。

经典的随机共振理论主要讨论的是双稳态随机共振模型，其中包含的主要理论有：驻留时间的分布特性、随机共振的响应过程、特征值研究、绝热消去理论等。

2 两个动力学方程

2.1 朗之万运动方程

朗之万运动方程讨论的是忽略重力条件下的布朗粒子。假设该粒子的质量为m，当该粒子在流体中运动时，主要分析两方面的作用力：（1）若布朗粒子的运动速度为v，运动会导致其受到周围分子的无序碰撞。该碰撞总体上作用结果为阻止布朗粒子的前进运动。可以定义这部分阻力为-av，该阻力将随着布朗粒子的宏观运动而持续；（2）从微观角度考虑，当布朗粒子受到无序碰撞时，碰撞力用F(t)表示，F(t)不随粒子的运动状态而改变。综合阻力-av和碰撞力F(t)两方面，可以得到粒子的运动方程如下：

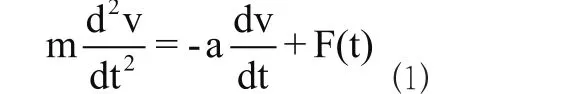
该方程描述了布朗粒子的运动情况。因为布朗粒子受到的无序碰撞力的随机性，粒子的运动方程为随机过程。

对公式（1）进行整理，方程两端同时除以m后可得[112]：

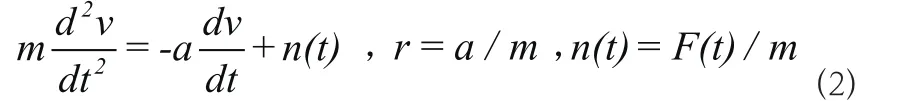
式（2）通常被称为线性朗之万运动方程，其中的r为阻尼系数，即单位质量的加速度。n(t)为布朗粒子受到无序碰撞所产生的随机噪声。

在（2）式的基础上，增加外场力f(t)对布朗粒子的作用，并将速度变量v一般化为x，（2）式可被写为：

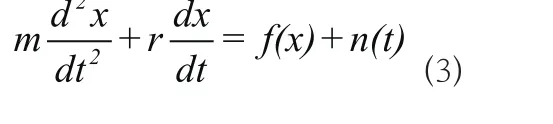
当f(t)为非线性的外场力时，（4）被称为非线性朗之万方程。后续的双稳态随机共振系统将基于非线性朗之万方程建立[113]。

2.2 福克-普朗克方程

非线性朗之万方程（4）中包含有随机项n(t)。因此当对（4）所描述的粒子运动状态进行研究时，通常讨论的是运动轨迹的各阶矩。非线性方程中相关变量的矩计算难度大，很难精确获取其统计特性。为此需要讨论相关随机变量的概率分布函数。由于非线性因素，（4）式中的变量x具有时变性，其概率分布函数也具有时变性。令变量x，在时间t的概率分布函数为ρ(x,t)。可以从朗之万方程推导出概率分布函数ρ(x,t)的方程[114]。

当系统中包含高斯白噪声时，可推导出概率分布函数ρ(x,t)的福克-普朗克方程：

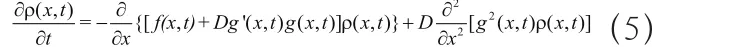
当系统中包含的噪声是加性高斯白噪声时，（5）简化为：

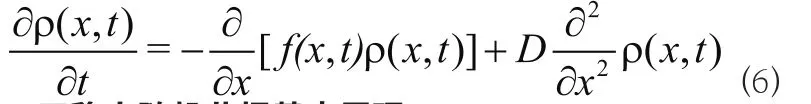
3 双稳态随机共振基本原理

3.1 动力学原理

双稳态随机共振属于非线性朗之万方程描述的一种特例，其对应的外场力为[115]

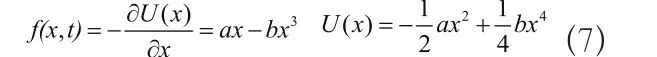
其中 称为势函数，a和b是两个重要参数，满足 ， ，其直接决定了双稳态随机共振的过程及发生条件。当从统计平均的意义上约去零均值的噪声n(t)时，非线性的朗之万方程改写为

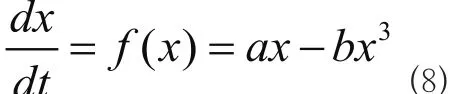
公式（8）描述了一维双稳态系统的动力学过程。从（8）可明显看出 是粒子运动的决定性因素。（8）式描述的系统的稳定点和不稳定点均可以通过求解 的极值点获得。极大值对应于不稳定点，极小值对应于稳定点。为求取极值点，对 求导可得：

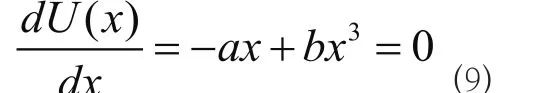
（9）的三个极值点为：

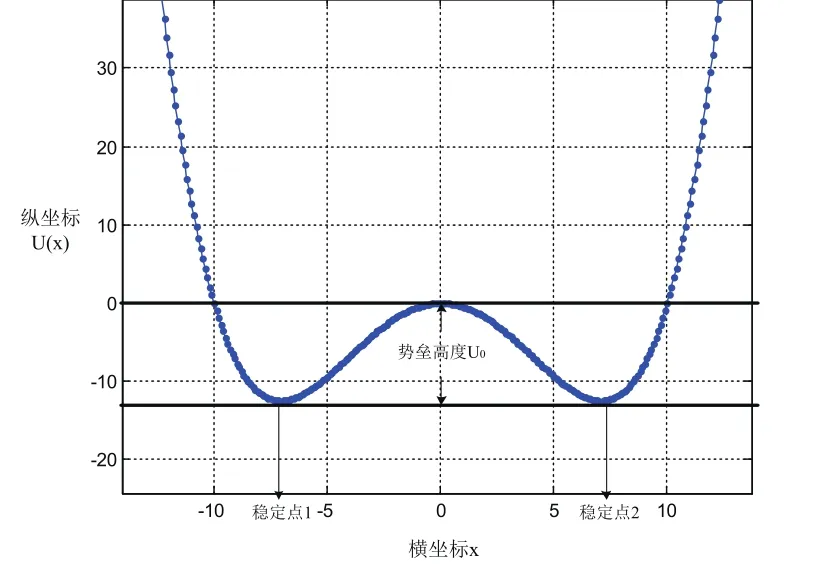
图 1 双稳态随机共振的势函数图

如图1所示是双稳态随机共振的势函数示意图，当一个粒子在这个势函数中运动时，假设初始时刻粒子在x=0点，当受到一个微弱的扰动时，粒子极易偏离不稳定点x=0，落入到稳定点。若扰动力使其偏移量Δx>0，则粒子倾向于落入到稳定点2，即x=若扰动力使其偏移量Δx<0，则粒子倾向于落入到稳定点1，即；若粒子处于稳定点1，当受到的力导致位移Δx<0，则随着Δx幅度增大，其阻力呈几何级数增大。从而最终使得粒子稳定在稳定点1附近。稳定点2同理。

3.2 双稳态随机共振

在应用于通信信号处理时，处理的对象通常可以假设为信号与噪声的叠加的结果。这与随机共振系统的输入相吻合，具体如下示意图：

图 2 信号处理系统过程图

令通信信号为s(t)，信道的加性噪声为n(t)。传统的信号处理系统就是如何降低噪声n(t)，从而使得输出x(t)尽可能与信号s(t)逼近。

图 3 双稳态随机共振系统的过程图

从图3可知，随机共振系统的输入输出与信号处理系统相同，因此二者可以相互统一。令n(t)表示系统的随机力，s(t)表示系统的驱动力，此时图3的随机共振系统可写为[116]：

（11）

通信信号通常需要利用载波进行调制，因此往往以正弦函数的形式出现：

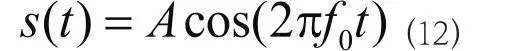
其中f_0表示信号载频，A(t)表示基带信号。将（12）代入（11）式可得：

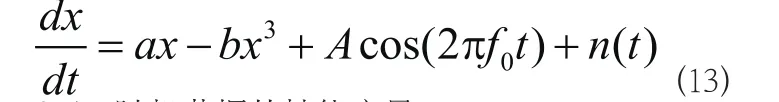
3.4 随机共振的性能度量

当信号经过随机共振系统后，如何评价输出的信号是个关键问题。通信中对于信号质量评价的一个重要参量是信噪比。在随机共振过程中，噪声的能量逐步被削弱，并转化为信号的能量。从而最终信号的能量增强，输出的信噪比远高于输入信噪比。利用信噪比评价随机共振进行信号处理的性能较为合适。信噪比计算公式为：

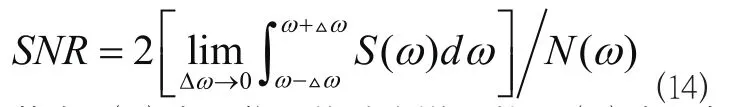
其中S(w)表示信号的功率谱函数，N(w)表示加性噪声的平均功率谱函数。（50）式中的极限求积分的过程较为复杂。当考虑到具体信号形式时，（50）式将进一步简化。假设输入为正弦信号，即，此时定义信噪比为：

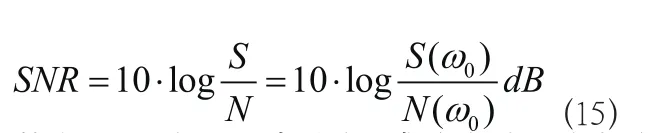
其中 表示噪声功率，求取方法是在频率 附近功率的平均值；同样地， 为信号在频率 附近功率的平均值。令系统输出信号的离散傅氏变换序列为,(k=0,1,……,L-1)：

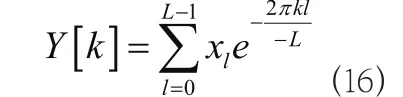
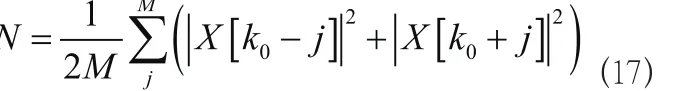
按照随机共振的绝热消去理论，双稳态随机共振系统的输出信号的信噪比为：

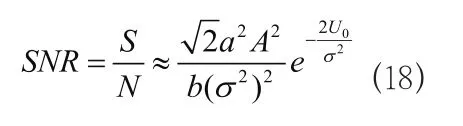
4 结束语

本文介绍了随机共振的相关基本理论。主要内容包括随机共振现象的动力学原理、随机共振的物理概念、随机共振过程的测度及相关参数等内容。