尾缘襟翼对风力机翼型气动特性影响研究

张 楠，李 春，王东华，叶 舟，郝文星

（上海理工大学 能源与动力工程学院/上海市动力工程多相流动与传热重点实验室，上海 200093）

近年来，为了更大程度地获取风能，降低单位风电成本，风力机单机容量及叶片尺寸不断增长［1］。叶片尺寸的增长使得叶片极限载荷和疲劳载荷增加，且使沿叶片展向载荷分布不均匀性增大［2］。尾缘襟翼能够改变翼型的气动特性，进而实现对叶片的载荷控制，且能够克服现有变桨技术惯性大，不能有效控制局部载荷波动的不足，被认为是降低叶片疲劳载荷最具可行性的气动控制部件［3］。但由于尾缘襟翼需要复杂的机械及控制系统驱动，且因其对疲劳载荷的控制需要较快的偏转速度，其可靠性较难保证，在风力机工程上应用较少［4］。随着风力机大型化以及变桨装置局限性的凸显，尾缘襟翼的研究一直被广泛关注。

美国Sandia国家实验室、荷兰Delft理工大学和丹麦RisDTU对风力机叶片尾缘襟翼进行了较多研究，显示了尾缘襟翼具有较好的降载效果［5］。Troldborg［6］以具有可变参数的尾缘襟翼Ris-B1-18翼型为研究对象，采用CFD软件优化尾翼形状、尺寸等，得出占弦比为5%～10%的尾缘襟翼为较优设计方案。Lackner等［7］对比分析了NREL 5 MW风力机模型分别采用独立变桨和尾缘襟翼后对疲劳载荷的影响，指出尾缘襟翼能够有效降低叶片疲劳载荷。Andersen［8］采用HAWC2软件模拟了动态失速模型和近尾流模型，验证了尾缘襟翼减少疲劳载荷的能力。叶舟等［9］以尾缘摆角为控制变量，研究了尾缘襟翼对翼型升阻特性的控制效果以及其对翼型周围流场特性的影响。以上研究主要关注的是尾缘襟翼气弹特性、控制策略和实现方式等方面，对襟翼附近的流动状态以及机理性研究不多，且对襟翼的减载效果也没有较直观的验证。

本文以NREL S809为基础翼型，采用翼型设计分析软件Xfoil中翼型设计模块实现翼型尾缘变形，研究变形襟翼对风力机翼型气动特性的影响，以及翼型气动特性随襟翼摆角的变化规律。采用Fluent软件模拟襟翼对翼型流场特性的影响，并分析其影响机理。以NREL PhaseⅥ风力机［10］为参考，对变化来流下襟翼对叶片的减载效果进行验证。

1 模型建立

1.1 尾缘襟翼模型

S809翼型尾缘变形情况如图1所示，图中：c为弦长。尾缘襟翼占弦比为10%，变形范围为± 20°（变形角顺时针为正）。

图1 尾缘襟翼变形及摆角示意图Fig.1 Schematic diagram of TEF deformation and tilt angle

1.2 计算模型

采用Xfoil软件进行翼型气动特性的计算。该方法将势流方程和边界层方程进行耦合，将翼型流动表示为表面上数量足够的点源和一个绕流环量，势流与边界层通过迭代耦合逐步进行修正，可实现边界层自由转捩［11］。该方法在进行风力机翼型计算时具有较高的准确度。Xfoil软件计算转捩模式为基于法的自由转捩，本文取临界系数。

采用基于有限体积法的CFD软件Fluent对翼型周围流场特性进行模拟，CFD计算模型采用C型结构化网格，计算域边界距前缘9倍弦长，距后缘20倍弦长。网格总数为21 000，其中翼型表面节点数经无关性验证后布置300个节点，第一层网格厚度根据湍流模型设置为2 ×10-3倍弦长（y+约为 30～100）。采用 SIMPLE算法对湍流模型RNG k-ε进行数值求解。RNG k-ε模型将壁面流动假设为充分发展湍流，采用标准壁面函数近似黏性底层与过渡层［12］。出口条件设为压力出口，翼型设为固壁无滑移条件。翼型计算区域及其周围网格分布如图2所示。

图2 翼型计算区域及其网格分布Fig.2 Computational domain and mesh of the airfoil

2 适用性验证

翼型主要气动特性包括升力系数、阻力系数以及升阻比，其升力系数、阻力系数CD和升阻比K可分别表示为

为了验证上述模型对风力机翼型气动特性分析的适用性，选用S809翼型进行二维气动特性计算，并将计算值与实验值进行对比分析，实验值来自 TU-Delft的实验［13］。计算时雷诺数，与实验时一致，攻角的范围为。CFD软件计算得到的来流速度为18 m·s-1，环境压强为标准大气压。

模拟计算值与实验值比较如图3所示，图中α为攻角。由图中可看出：α为-5°～11°时，CL的Xfoil软件计算值与实验值吻合较好，无论在附着流区还是在失速区［13］，其最大偏差均不超过6%；在附着流区，CL的CFD软件计算值与实验值也非常吻合，在失速区由于流动较复杂且存在非定常现象，两者存在一定误差。因Xfoil软件计算时采用的是自由转捩模型，在附着流区CD计算值与实验值非常吻合，在失速区受流体分离影响，计算值稍小于实验值；在附着流区CD的CFD软件计算值略高于实验值，在失速区略小于实验值，整体变化趋势较为吻合。可见，采用全湍流模型模拟翼型气动特性误差主要体现在CD。因CD较小，且与模拟趋势较为吻合，故采用全湍流模型模拟翼型气动特性时的误差是可以接受的。通过对比分析可知，利用Xfoil软件分析风力机翼型二维流动具有较高的精度，且计算速度较快。CFD软件用于风力机二维流动分析时，气动特性计算值一定范围内需要修正，但可体现出翼型流场流动特点，在对流场特性的分析中具有优势。

图3 模拟计算值与实验值比较Fig.3 Comparison between the simulation results and experimental ones

3 结果与分析

3.1 固定摆角尾缘襟翼攻角特性

图4为采用Xfoil软件计算得到的S809原始翼型（即尾缘襟翼摆角θ = 0°）及其襟翼摆角分别为10°、-10°的翼型气动特性随攻角α的变化。

由图 4（a）中可知，α 为-5°～20°时，三种不同襟翼摆角翼型的CL均随α增大呈增大趋势：当α为-5°～6°时呈线性增长，为流动附着区；当 α为 6°～20°时增长减缓且个别翼型在α为15°之后有所降低，此阶段为非线性阶段，为流动分离区，翼型处于失速状态。襟翼摆角为10°的翼型CL总体上大于原始翼型的CL，且在α为-5°～6°（流动附着区）时增幅较大，约为0.35。原始翼型 CL由 0增加到最大值 1.0时α为0°～15°，而在此升力系数范围内襟翼摆角为 10°的翼型的 α 为-5°～5°。襟翼摆角为-10°的翼型CL总体上小于原始翼型CL，且在流动附着区减幅较大，约为0.35。三种翼型中襟翼摆角为10°的翼型随α增大率先进入非线性阶段，此时CL已达1.0，摆角为-10°的翼型进入非线性阶段稍滞后于原始翼型，此时CL约为0.5。

图 4（b）为三种翼型 CD随 α的变化。当α为-5°～5°时，三种翼型CD相差不大，且均随α增加变化不大；当α为5°～20°时，三种翼型CD均随α增大而增大，且襟翼摆角10°翼型CD总体上大于原始翼型，摆角为-10°的翼型CD总体上小于原始翼型。图4（c）显示出襟翼位于正摆角时翼型最大升阻比其他两种翼型的大。由于提前进入了非线性阶段，最大升阻比所对应攻角也较小，位于负角度时最大升阻比其他两种摆角时小，最大升阻比对应攻角较大。

由以上分析可知，相对于原始翼型，正摆角襟翼翼型能够在满足相同CL要求时降低CD，同时能够提供较大的升阻比，进而降低叶片载荷。而对于负摆角襟翼翼型，整个攻角范围内CL低于原始翼型，CD总体上低于原始翼型。这为降低叶片整体载荷和局部载荷提供了一种解决方案。

图4 不同摆角襟翼翼型气动特性随攻角的变化Fig.4 Variation of flap airfoil aerodynamic performance at different tilt angles with angle of attack

3.2 尾缘襟翼摆角特性

通过摆角确定襟翼的位置是控制襟翼的直接方法。由图4（c）中可看出，S809翼型失速角位于6°附近，此时CL较大，CD较小，升阻比最大。当选取6°为襟翼摆动过程中的攻角时可以很好地反映出当翼型处于最大升阻比时，襟翼摆角对翼型气动特性的影响。Xfoil软件计算的攻角为6°时翼型气动特性随襟翼摆角的变化如图5所示。襟翼正角度变化时，随着摆动幅度增大，翼型CL增大，CD仅在摆角大于6°时有所增加；襟翼负角度变化时，随着摆动幅度增大，CL降低，CD略有升高；θ为-10°～6°时，CL随摆角线性变化，超过此范围时，CL变化趋势有一定的减缓。总体来看，随着θ的增大，CL增加，CD变化不大。这表明，襟翼能够有效调节翼型的气动特性，进而控制叶片疲劳载荷和局部载荷。

根据翼型表面静压分布和流线分布可以看出尾缘襟翼对翼型流场特性的影响。流场特性采用CFD软件模拟。限于篇幅，本文仅给出θ分别为10°、-10°的翼型和原始翼型在攻角为6°时的静压分布和流线分布，如图6所示。由图6（a）中可看出，随θ的增加，翼型吸力面负压区域扩大并向后扩展，负压强度也随θ增加而增加；压力面负压区域随θ增加而减小，负压强度也逐渐减小。尾缘θ为10°时，可以看出压力面的负压区几乎消失。这反映出随θ增加，上、下翼面压差增加，进而导致翼型升力系数增加。由6（b）中可以看出，襟翼的摆动导致翼型尾缘的流线方向发生改变。当襟翼摆角为10°时，尾缘出现小范围漩涡，流体流动出现分离。这也验证了本文3.1节中的结论：较大襟翼摆角的翼型随着攻角增大率先进入非线性阶段。

图6 攻角为 6°时翼型周围流场特性Fig.6 Flow field characteristics of airfoil at angle of attack of6°

4 实用性验证

尾缘襟翼主要用于降低叶片疲劳载荷与局部载荷，对翼型升阻力的影响并不能直观地反映其对叶片的减载效果。本文从叶素角度以NREL PhaseⅥ风力机［12］为参考，验证阵风下尾缘襟翼对叶素在挥舞（x轴方向）、摆振（y轴方向）方向的减载效果。

NREL Phase Ⅵ风力机额定功率为19.8 kW，叶片展长为5.03 m，参照实际建立了该叶片某位置处叶素受力模型，叶素展长为1 m。风力机叶素受力模型如图7所示，图中：v为来流风相对速度；u为叶素在风轮回转平面内运动速度；w为来流风相对叶素速度；β为桨距角；为FL和FD在x轴上的分力之和，与来流风向垂直，称为驱动力，使桨叶旋转做功；为FL和FD在y轴上的分力之和，与来流风向平行，称为轴向推力，通过塔架作用在地面上。

文献［10］中风力机模型的叶片产生的最大功率区域在 0.75倍展长附近，该区域 β = 0，c = 0.5 m，v = 11 m·s-1，额定工况下 α = 6°。阵风模型与攻角变化如图8（a）所示，v以额定风速经过0.4 s上升为16 m·s-1。由于存在较大的惯性，风力机转速来不及发生变化，即u不变。由图7中可看出，v增加将导致w大小和方向发生改变，进而使叶素攻角发生改变。图8（b）为叶素在阵风下的受力情况，挥舞方向受力由额定工况下0.27 kN增大到0.45 kN，增幅为0.18 kN，约为额定工况下的67%；摆振方向受力由额定工况下2.86 kN增大到3.34 kN，增幅为0.48 kN，约为额定工况下的17%。由此可知，风速短时间快速增加会使叶素在挥舞和摆振方向受力不同程度地增加，其中在挥舞方向增加较为显著。

图7 风力机叶素受力模型Fig.7 Force model of the wind turbine blade element

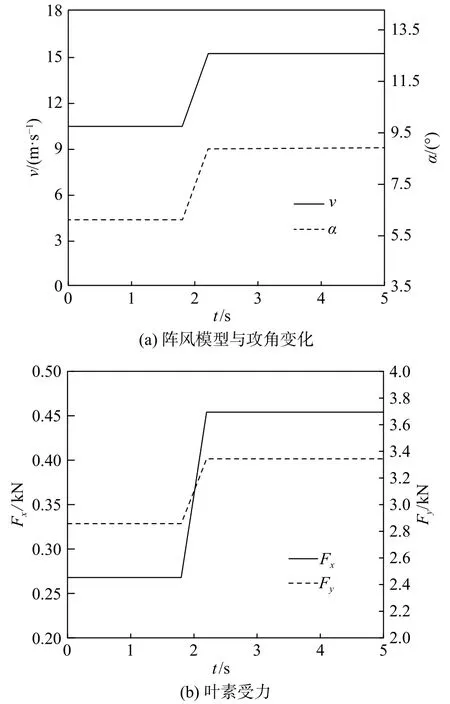
图8 阵风下叶素受力情况Fig.8 Force of the blade element in a gust of wind

尾缘襟翼对翼型升阻力系数具有很好的调控能力，且由于其反应快，具有很好地结构和安全特性，可有效降低叶片疲劳载荷和局部载荷［3］。由图 8（a）中可知，风速增大后叶素 α变为8.74°，襟翼将在此状态下动作进而控制载荷。图9（a）为α = 8.74°时襟翼摆动过程中的升阻力系数。由图中可知，襟翼向负角度摆动时，升阻力系数均有下降。摆角摆至-18°时，CL已由0.98下降至0.50，降幅约为51%；CD由0.016 5降至0.010 5，降幅约为36%。襟翼对翼型升阻力系数的控制最终体现为叶素受力的变化。图9（b）为襟翼摆动时叶素挥舞、摆振方向上气动力的变化。由图中可知，襟翼向负角度摆动时，随着摆动幅度的增加，挥舞、摆振方向上的受力均减小，襟翼向正角度摆动时反之。当襟翼摆动至-18°时，挥舞受力由最初的0.45 kN降为0.23 kN，摆振方向受力由3.34 kN降至1.71 kN；当襟翼摆动至-14°时，挥舞受力为2.76 kN，此时与叶素阵风之前挥舞受力相差不大，摆振方向受力为2.07 kN，小于阵风之前摆振受力2.86 kN。

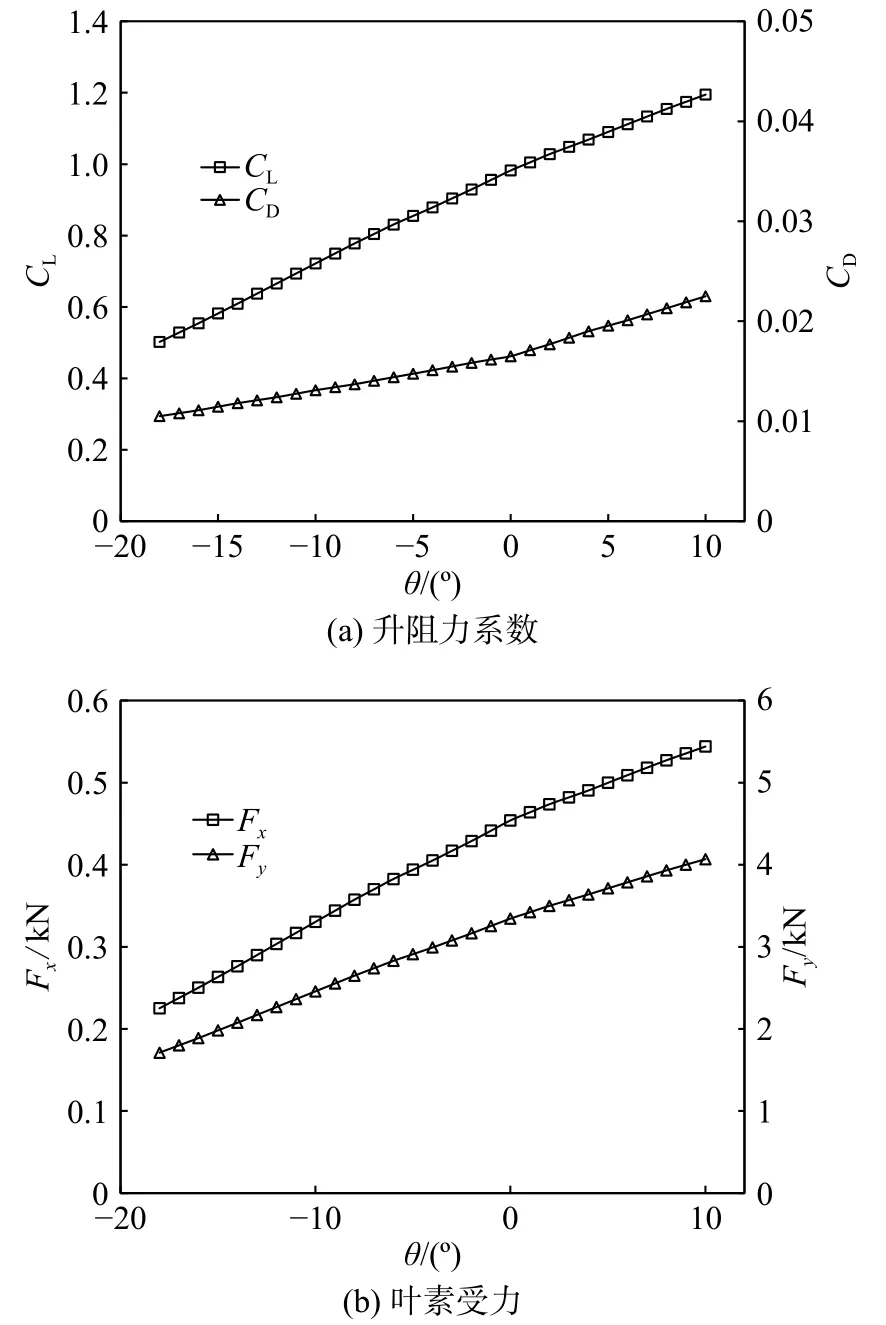
图9 升阻力系数、叶素受力随襟翼摆角的变化Fig.9 Variation of lift and drag forces and the blade element force with flap tilt

由此可知，襟翼有效地调整了叶素在阵风下的载荷，风速增加后能够及时使挥舞方向受力降至最初状态，在控制叶素载荷的同时保证了风力机功率的稳定，摆振方向受力也得到了控制，甚至低于最初状态，进而能够减小叶片摆振幅度，有效地改善了叶片的工作状态。

5 结 论

通过对尾缘襟翼进行建模，分析了襟翼对翼型气动特性的影响及其机理，进而对襟翼的减载效果进行验证，得出以下结论：

（1）襟翼摆动位置对翼型气动特性影响较大。襟翼处于正摆角时，升阻力系数均较原始翼型增大，在提供相同升力系数的同时阻力系数可较原始翼型小；襟翼处于负角度时，升阻力系数均较原始翼型减小。这为风速增大时降低叶片载荷提供了一种解决方案。

（2）翼型处于最大升阻比状态时，襟翼正角度摆动。随着摆动幅度的增加，翼型升力系数增加，负角度摆动时则反之。阻力系数整个过程中略有增加，整体增幅不大。

（3）襟翼摆动可影响翼型表面的静压分布，改变翼型上、下表面压差，进而影响翼型升阻力系数。在攻角增大时与原始翼型相比，正摆角襟翼翼型提前进入失速状态，负摆角襟翼翼型则反之。

（4）风速突然增大会使叶素攻角发生改变，挥舞、摆振方向受力均不同程度地显著增加。改变襟翼摆角可快速有效降低挥舞、摆振方向受力，进而控制并减小叶片载荷，保持功率稳定。