曼德尔布罗特——海岸线的长度
2018-10-18曹则贤
曹则贤

记得有一首很抒情的歌唱道:“林中的小路有多长?只有我们漫步度量。”林中的小路有多长?一般人不会认为这是一个成问题的问题。翻开地理书,就能看到“我国有长达多少多少千米海岸线”的说法。海岸线真有确切的长度吗?1967年,曼德尔布罗特在《科学》杂志上发表了题为《大不列颠的海岸线有多长》(How Long Is the Coast of Britain? Statistical Selfsimilarity and Fractional Dimension)的论文,明确指出海岸线的长度是一个依赖于测量所用标尺的量。相关问题的研究引入了一个崭新的数学分支—分形几何。
曼德尔布罗特(Benoit B. Mandelbrot,1927~2010),数学家,出生在波兰,后来先后定居在法国和美国。受其数学家叔叔的影响,曼德尔布罗特从小就热爱数学。在求学经历中,曼德尔布罗特曾受教于大数学家尤利亚(Gaston Julia)、冯·诺依曼(John von Neumann)。曼德尔布罗特后来在美国凭借替国际商业机器公司(IBM)工作的便利,成了最先使用计算机图形功能创造分形几何的人。当然,这也与他的老师尤利亚引入的一种特殊的集合有关。
尤利亚集合与复函数的迭代有关。例如,考察函数fc(z) = z2 + c,其中c是一个常复数,z是复变量。把函数fc(z)当成新的变量z代到方程的右边去,可以研究这个函数的迭代性质。如果某个区域内的z经过迭代算法还保留在这个区域内,则这个区域属于复平面内的Fatou集合。Fatou集合以外的区域就是尤利亚集合。尤利亚集合是处处非稠的集合(通俗地说,就是麻将牌里的“十三不靠”),因此具有非常迷人的外观。
对于fc(z) = z2 + c这样的迭代函数,可引入曼德尔布罗特集合。从图中可以看出,曼德尔布罗特集合的边界具有越来越精细的、递归的细节,也就是说你将选定的部分不断地放大,会发现同样的细节会不断再现。对局部的放大会重复发现图形整体的形状,即是说图形具有自相似的结构。
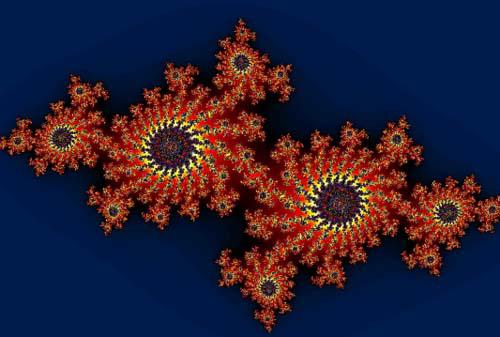


1975年,曼德尔布罗特创造了“分形”(fractal)一词,用来描述那些具有自相似结构的几何体。聪明的读者可能已经注意到,因为曼德尔布罗特集合是由迭代算法的结果加以定义的,因此所谓的曼德尔布罗特集合之图形化表示具有自相似结构是自然而然的事情,算法的迭代和所得图形的自相似,这两者是有内在联系的。具有自相似结构的事物在菜市场就能见到,比如宝塔菜,可以看到几个大小层次上的花瓣结构都是一样的螺旋状的。当然了,宝塔菜不仅有自相似结构,其结构花样还是斐波那契斜列螺旋(Fibonacci parastichous spirals),因此更显神奇。
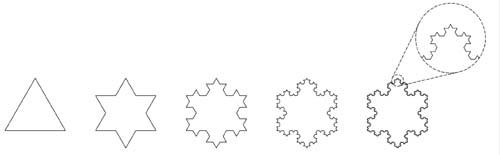
为了更好地理解分形的概念,我们考察一个简单点的例子。如下图,从一个正三角形出发,把其每边的中间三分之一去掉,但以这去掉的部分为基准往外构造一个正三角形,则这新的两边就替代被去掉的部分完成了去掉部分的连接。对所有某个尺度上存在的线段进行上述操作,不断地重复下去,就能得到所谓的科赫曲线或者科赫雪花。明顯可看出,随着构造不断往下个层面进行,这个图形的周长也在不断增大。实际上,每往下一个层面,周长都增加到原来的4/3倍。
曼德尔布罗特注意到类似科赫雪花样的曲线在别的领域也能见到,比如人们非常熟悉的海岸线。海岸线虽然不会像科赫曲线那样具有严格的自相似结构,但确实是足够不规则的。可以肯定的是,使用越小的尺子,量得的海岸线长度就越长。曼德尔布罗特引入了分形几何和分数维度的概念,认为一类具有自相似结构的几何体,其维度是一个非整数,比如科赫雪花的维度就约是1.26。作为对照,直线、圆周是一维的,平面规则图形如三角形、菱形是两维的,而球体、四面体这样的规则结构是三维的,维度都是整数。分形几何在物理学、化学、经济学、地球科学、气象学等领域里都找到了许多有价值的应用。
海岸线多长的问题,实际上牵扯到了测量这一物理学最重要的问题。以标尺进行的长度测量,测量对象在标尺的尺度之上出现显著变化才是允许的、可容忍的。一条海岸线,可以简化为折线,它出现拐点的特征越小,则允许的标尺尺度也应该越小。这在提醒我们,不存在先验的测量设备和测量方法。那些能得出有价值结果的物理实验,其所使用的设备和方法是在对具体问题的研究过程中慢慢演化出来的。某种程度上可以说,实验和理论是一体的,都是物理知识体系的有机组成部分,是相互砥砺才获得正确性的。
本文选自《一念非凡—科学巨擘是怎样炼成的》。该书由外语教学与研究出版社出版,入选我社“中华优秀科普图书榜”2018年第一季度“成人原创”榜单。
温馨提示:若你牵着蹒跚学步的小孩儿沿着羊肠小道这样的分形结构散步时,请你一定要耐心地等他,因为在他的小脚下,路确实更长。
