岩石物理建模在东胜气田横波速度预测中的应用

2018-10-18李灿

石油化工应用 2018年9期

李灿

（中国石化华北油气分公司勘探开发研究院，河南郑州 450006）

鄂尔多斯盆地东胜气田位于鄂尔多斯盆地杭锦旗地区，地质构造横跨伊陕斜坡与伊盟隆起。近年来，随着勘探的精度要求越来越高，油气勘探方向逐渐向隐蔽致密岩性油气藏转变，利用三维地震叠前反演技术在岩性勘探中得到了广泛的应用，而横波信息是这项技术不可缺少的要素。由于技术及成本上的原因，大多数测井都是常规测井，缺乏横波资料，因此，需要应用常规测井和岩石物理分析数据对横波数据进行拟合。在以往的研究过程中，大多是利用研究区内实测纵、横波时差曲线间存在的函数关系，进行回归分析，建立经验公式；或者直接应用Castagna公式，进行横波曲线的拟合。对比实际横波资料发现，经验公式预测的横波曲线在含油气层段误差较大，并且无法进行流体替换和流体敏感性分析。岩石物理建模可以建立起弹性属性与岩石物理属性之间的关系，是通过研究岩石岩性、孔隙结构、流体性质、地层温度和压力等特征来定量拟合横波曲线的有效方法[1，2]。

1 井震一致性处理

在进行岩石物理建模之前，首先要对测井曲线进行质量控制，检查测井曲线的质量，主要是进行测井曲线的环境校正、测井曲线的一致性处理，体积模型的一致性。测井曲线一致性，主要是检查在研究区内相同或者相近岩性是否具有相近的测井特征[3]。体积模型的一致性主要检查测井地层评价结果是否是面向地震储层预测的岩石物理建模所需求的。

图1 研究区目的层段校正前中子-声波交会图Fig.1Before correction neutron-sonic intersection diagram of the target layer in the study area

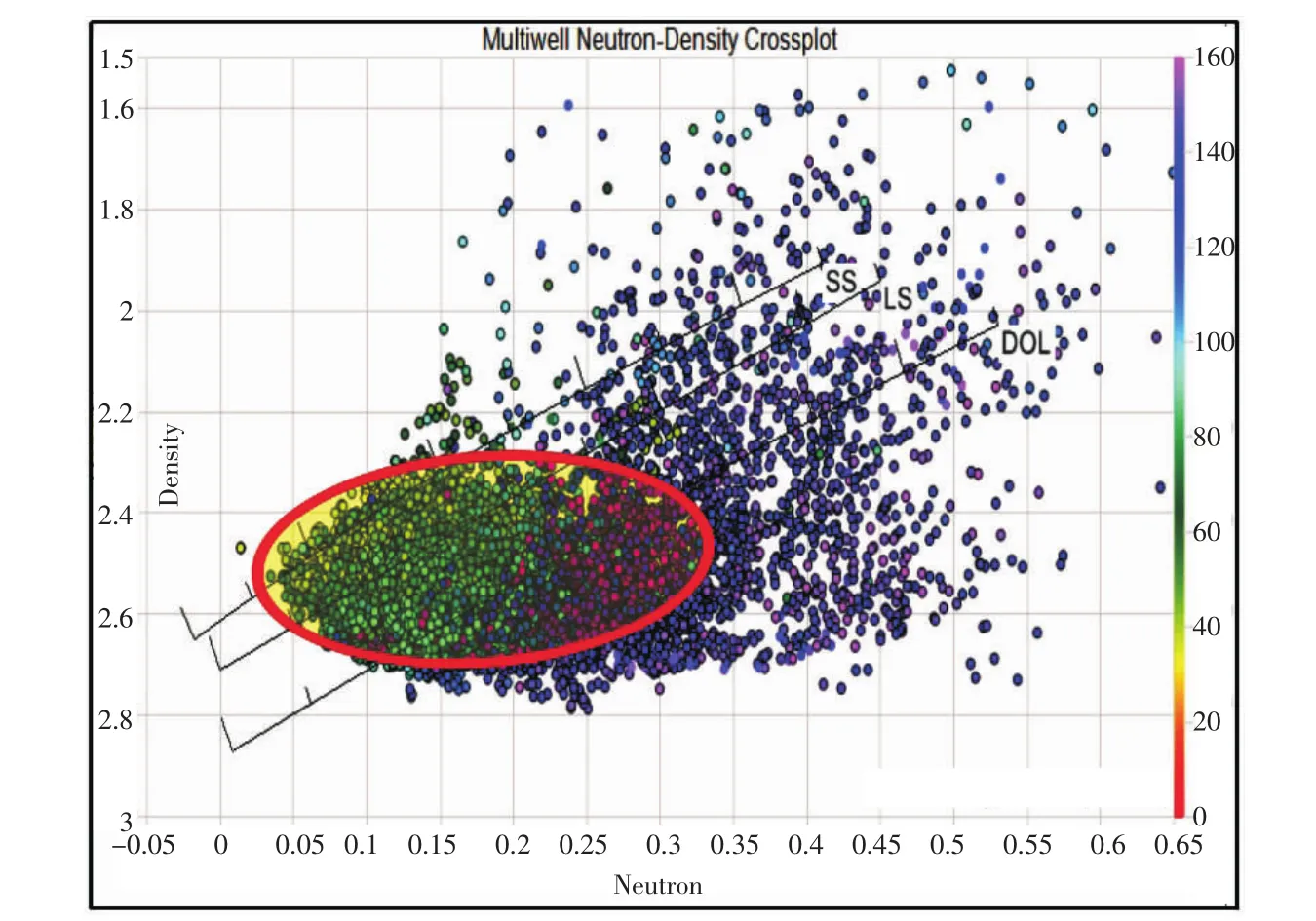
图2 研究区目的层段校正前中子-密度交会图Fig.2 Before correction neutron-density intersection diagram of the target layer in the study area

1.1 测井曲线的环境校正

岩石物理建模中参与体积模型计算的曲线主要是自然伽马曲线、三孔隙度测井曲线，东胜气田主要目的层为下石盒子组，在钻井过程中，泥岩段井眼垮塌较为严重，由于受井眼环境的影响，中子、密度、声波均存在不同程度的失真。曲线校正前的中子-密度交会图、中子-声波交会图（见图1、图2），在井眼垮塌处，由于扩径的影响在测井过程中会造成中子测井变大、密度测井变小、声波测井值增大。由于测井曲线的失真，会造成对原状地层情况的认识有偏差，因此需要进行测井曲线的井眼环境校正。

本次对研究区进行井眼环境校正的过程采用多元线性拟合的方法，所遵循的原则是选取井眼环境较好、与目的层相近或者相同的岩相与岩性、饱和流体信息，且相对较长的一段进行测井曲线的相关分析，计算相关关系模型。通过模型来拟合井眼垮塌处的测井曲线来进行校正，对校正后的曲线首先进行交会图法质控，校正后的中子-密度交会图、中子-声波交会图（见图3、图4）。通过对井眼垮塌处测井曲线的校正，使得散点数据更加收敛，更符合实际地质情况。

图3 研究区目的层段校正后中子-声波交会图Fig.3 After correction neutron-sonic intersection diagram of the target layer in the study area

图4 研究区目的层段校正后中子-密度交会图Fig.4 After correction neutron-density intersection diagram of the target layer in the study area

对校正的单井数据进行合成地震记录与井旁地震道数据作对比，测井曲线环境校正前的合成地震记录与井旁地震道的同相轴与能量关系差异比较大；测井曲线环境校正后的合成地震记录与井旁地震道同相轴基本都能匹配，能量关系匹配较好，测井曲线环境校正后更加符合真实的地层情况。

1.2 体积模型的一致性

常规测井所解释的体积模型不能满足岩石物理建模的需求[3]。在砂岩储层中，常规的测井解释只对储层段的饱和度与孔隙度进行解释，而对非储层段没有进行解释；岩石物理建模需求全目的层段的数据，因此要对目的层段的体积模型进行解释。研究区通过求取泥岩的密度、中子、声波的骨架点值然后采用基于powerlog的最优化测井解释进行总孔隙度、泥土含量、矿物含量的计算，其结果用于岩石物理建模。常规测井体积模型与最优化测井解释体积模型对比图（见图5），其中孔隙度（POR）、声波时差（ACC）、含气饱和度（SWO）、泥质含量（SH）、砂岩含量（SAND）为常规测井解释结果，总孔隙度（PORT）、重构声波时差（RACC）、含水饱和度（SWC）、黏土含量（VCLAY）、石英含量（VQUA）为最优化测井解释结果。通过对比发现在储层段的孔隙度、饱和度与最优化测井解释的孔隙度匹配度较高，体积模型基本一致。因此最优化测井解释结果能够用于岩石物理建模。

2 岩石物理建模

Xu－White模型是一种适合致密砂岩地层的岩石物理建模模型，结合Gassmann方程考虑流体影响和Kuster-Toks模型考虑孔隙形状。是一种利用孔隙度、孔隙形状、黏土含量估算砂、泥岩地层纵、横波速度的方法[4]。岩石物理建模核心流程主要分为四个部分（见图6）：第一部分为基质骨架等效弹性参数的计算，第二部分为干岩石的等效弹性参数计算，第三部分为混合流体的等效弹性参数计算，第四部分为饱和流体岩石的弹性参数计算。

图5 研究区某井常规测井体积模型与最优化测井解释体积模型对比图Fig.5 Comparison of the conventional logging volume model and the optimized logging interpretation volume model of a well in the study area

图6 岩石物理建模流程图Fig.6 Rock physics modeling flow chart

2.1 基质的等效弹性参数计算

骨架部分主要包括泥岩骨架、砂岩骨架、石膏等矿物；计算方法采用Voigt-Reuss-Hill平均模型骨架混合的方法；其方法原理假设f1为矿物1的体积组分含量，f2为矿物2的体积组分含量，f1+f2=1，M1为矿物1的体积模量或者剪切模量，M2为矿物2的体积模量或者剪切模量，Voigt平均极限模型[5]可以表现为公式（1）：

Reuss平均模型[6]可以表示为公式（2）：

根据 Voigt模型估算的是弹性模量的上限，而Reuss模型估算的是弹性模量的下限。Hill在前人研究基础上建议对 Voigt上限值和 Reuss下限值取平均值[7]来求取基质的弹性参数，因此Voigt-Reuss-Hill平均模型可表示为公式（3）：

2.2 干岩石的等效弹性参数计算

在基质的弹性参数计算的基础上加入孔隙度则可以进行干岩石的弹性参数计算，方法采用微分等效介质模型通过向固体矿物相加入椭圆形的包含物相（孔隙）来模拟双相混合物。该模型中要明确区分选择介质A为基质矿物，介质B为包含物还是介质B为基质矿物，介质A为包含物，因为介质A和B选择的不同会导致结果的不同。

微分等效介质模型的等效体积模型K与等效剪切模量μ的耦合公式[8]：

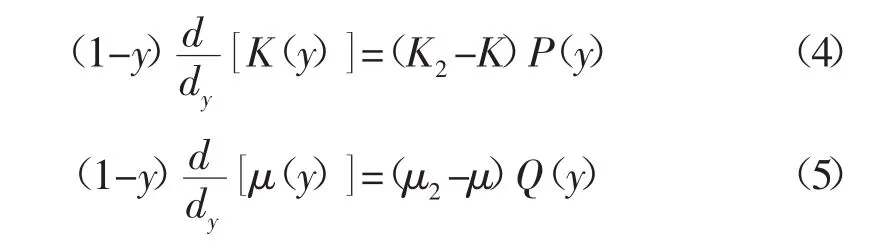
K（0）=K1、μ（0）=μ1，式中：K1、μ1-基质矿物的体积模量和剪切模量；K2、μ2-加入包含物的体积模量和剪切模量，对于孔隙包含物y为孔隙度；P、Q系数从不同孔隙形状的长宽比计算公式中得到。

2.3 混合流体的等效弹性参数计算

采用Batzle-Wang公式[9]计算得到在一定温度、压力、矿化度条件下的单相流体的体积模量和密度，然后用Brie模型得到流体混合后弹性参数。Brie模型公式可以表示为：

式中：Kw-水的体积模量；Kg-气体的体积模量；Sw-含水饱和度；e-经验常数。

2.4 饱和流体岩石的等效弹性模量计算

采用Biot-Gassmann体积模量和剪切模量方程分别为公式（7）和公式（8）：

式中：Ksat-饱和流体岩石的体积模量；Kdry-干岩石的体积模量；Km-基质的等效体积模量；Kfl-混合流体的体积模量；φ-孔隙度；μsat-饱和流体岩石的剪切模量；μdry-干岩石的剪切模量。

3 横波预测

在测井曲线环境校正、一致性处理、测井地层评价重新解释的基础上，优化石英与黏土的骨架值及石英与黏土矿物的宽长比，建立岩石物理模型，进行横波预测，其结果（见图7），图7中为研究区某口有实测横波曲线的井，其中VP、VS、PIMP分别为经过环境校正后的实测纵波速度曲线、横波速度曲线、纵波阻抗曲线，VPM、VSM、PIMPM分别为预测纵波速度曲线、横波速度曲线、纵波阻抗曲线。预测曲线与实测曲线具有很高的相关性，因此横波预测可信度较高。

4 结论

岩石物理建模是地震岩石物理研究的核心内容，模型的选择是关键，在致密砂岩储层中Xu-White模型较为适合。在用Xu-White模型进行砂泥岩地层岩石物理建模的过程中，常规的测井解释只对储层段的饱和度与孔隙度进行解释，而对非储层段没有进行解释；岩石物理建模需求全目的层段的数据，因此要对目的层段采用最优化测井解释的方法对体积模型进行解释并应用于岩石物理建模，最终得到了较好的横波预测曲线。