混合型广义犹豫模糊语言多准则群决策方法

任 剑，王坚强，成鹏飞，胡春华

(1.湖南商学院 新零售虚拟现实技术湖南省重点实验室，湖南 长沙 410205；2.湖南商学院 湖南省移动电子商务协同创新中心，湖南 长沙 410205；3.中南大学 商学院，湖南 长沙 410083；4.湖南科技大学 商学院，湖南 湘潭 411201)

0 引言

在实际决策中，由于对象的复杂性、环境的不确定性和认知的不完全性，决策者在刻画模糊数的隶属度时常犹豫不决。一些学者致力于程式化、规范化现象。Torra[1]提出犹豫模糊集，指出犹豫模糊数的可能隶属度是[0,1]的一个子集;Xu等[2]给出犹豫模糊集的形式化定义，探讨其距离和相似度的测算方法;Rodríguez等[3]采用一个有限、有序、连续的语言标度子集表示犹豫模糊语言集;Lin等[4]提出由犹豫模糊语言数和可能隶属度组成的犹豫模糊语言集，前者为一个语言标度，后者为上的一个非空有限子集;Meng等[5]提出由犹豫模糊语言数和可能隶属度的元组组成的犹豫模糊语言集，并定义混合信息集成算子;Liao等[6]给出犹豫模糊语言集的距离和相似度测算方法;Wang等[7]构建了犹豫模糊语言集的Outranking关系分析方法，允许偏好关系间具有不可比性和非传递性，以解决信息失真问题;Wang等[8]提出区间犹豫模糊语言集,犹豫模糊语言数的可能隶属度为若干个上的区间数的集，并定义信息集成算子;Lee等[9]定义了犹豫模糊语言集的可能度比较关系和信息集结算子。犹豫模糊语言集能较好地刻画定性、定量均不确定的决策信息，已应用于群决策[10]或多准则决策[11]问题求解。上述成果从问题情境出发，提出不同种类的犹豫模糊语言集并进行特定处理，没有提出统一的概念范畴和计算方法，缺乏对其共同特征及关联关系的深入分析。

近年来，得分函数在模糊多准则决策中被广泛运用。Chen等[12]利用得分函数处理基于Vague集的模糊多准则决策问题;Liu等[13]在点算子和估值函数的基础上，提出得分函数来解决直觉模糊多准则决策问题;徐泽水[14-15]定义了区间直觉模糊数的得分函数，并提出得分矩阵;Chen[16]基于点算子提出乐观得分函数和悲观得分函数，并设计出结果导向的直觉模糊多准则决策方法;Wang等[17]将交叉熵引入得分函数的定义中;Chen等[18-19]将区间直觉模糊数的得分函数应用于多准则群决策中;Pei等[20]在直觉模糊集的得分函数中考虑了隶属度和非隶属度的相对重要系数;Wang等[21]定义了区间直觉模糊集的前景得分函数;Chen等[22]总结并定义了直觉模糊集和区间直觉模糊集的加权得分函数;Wu等[23]定义了区间直觉梯形模糊数的得分期望函数;Agarwal等[24]定义了泛化直觉模糊软集的得分函数;Wang等[25]在得分函数中考虑心理参数，以反映决策者的风险态度;Hu等[26]定义了二型犹豫模糊集的得分函数。上述研究主要集中在直觉模糊多准则决策领域，通过隶属度和非隶属度间的差异来描述得分函数。语言标度的下标值是犹豫模糊语言集的重要参数，反映了评价结果的优劣程度，通过对语言标度的下标值进行集结，能够较好地定义不同犹豫模糊语言集的得分函数。

目前，复杂模糊多准则群决策已经成为研究热点，主要有语言模糊多准则群决策[27]、直觉模糊多准则群决策[28]、中智模糊多准则群决策[29]、二型模糊多准则群决策[30]、毕达哥拉斯模糊多准则群决策[31]、犹豫模糊多准则群决策[32]、犹豫模糊语言多准则群决策[33]等，这些研究对经典模糊集的值域或隶属度进行了拓展。模糊混合多准则群决策是一种更复杂的群决策问题，“混合”主要表现为两种情形：①利用不同决策方法的特性进行组合决策[34]；②准则值为不同类型的不确定性信息[35]。现实中，由于知识经验和习惯偏好的差异，不同的领域专家可能采用不一样的犹豫模糊语言集表示准则赋值，并给出不一样的专家权重向量或准则权重向量，针对这一复杂决策情形，目前还缺乏相关研究。

综上所述，现有的犹豫模糊语言混合多准则群决策研究没有提出普适性较强的统一决策模型，且欠缺对不同形式的专家权重向量或准则权重向量的综合分析，不利于该理论的推广和应用。因此，本文针对各领域专家的不同行为偏好，综合考虑不同类型的犹豫模糊语言集，统一定义广义犹豫模糊语言集，并对其性质、运算等进行系统研究，兼顾不同形式的专家权重向量或准则权重向量，提出一种基于得分函数与排序得分的混合多准则群决策方法。

1 广义犹豫模糊语言集

1.1 语言标度集

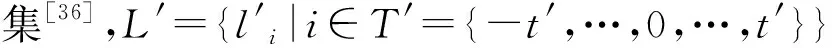
在语言模糊决策时，决策者通常利用L′对方案进行赋值，运用L″对方案赋值进行运算[37]。一些学者探讨了拓展语言标度集的模糊语义表征和语言语法规则[38]。

为方便后续运算，定义符号⊕，⊖，⊗表示语言标度之间、清晰数与语言标度之间、区间数与语言标度之间的加、减、乘运算；符号+，-，·，/，∑表示清晰数之间、清晰数与区间数之间[39]、区间数与区间数之间[39]的加、减、乘、除、连加运算。

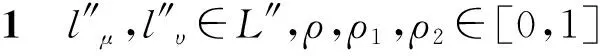
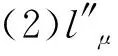
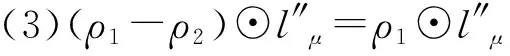
1.2 广义犹豫模糊语言集的定义

定义1广义犹豫模糊语言集(GHFLS)。X={xi|i∈M={1,2,…,m}}是一个论域，H={hk|hk∈[0,1]∨hk⊆[0,1],k∈N={1,2,…,n}}是一个可能隶属度集，hk(k∈N)为清晰数或区间数，则称LGHFLS={xi,{⊆H,j∈T′}|xi∈X}是一个GHFLS，其中：j表示对称语言标度集中元素的下标值，表示L′中下标值为j的元素，Hij表示对应的可能隶属度集，⊆H,j∈T′}表示广义犹豫模糊语言数集(GHFLNS)(i∈M)。

设G(·)是一个集合的基数函数，LGHFLNS存在以下4种常见情形：

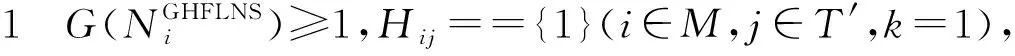
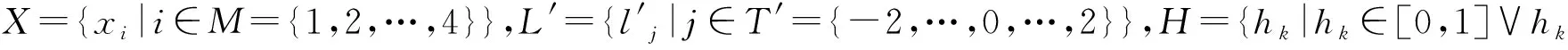
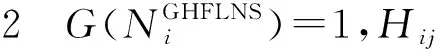
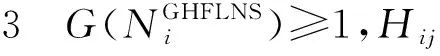
显然，情形2是情形3的特殊情况。

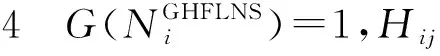
本文重点讨论以上4种常见情形。GHFLS可以是不同情形的混合。

1.3 广义犹豫模糊语言集的运算

设有两个GHFLS：

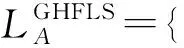
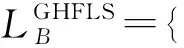
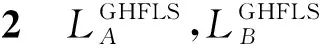
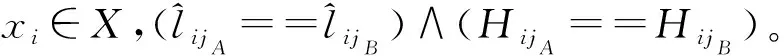
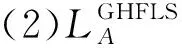
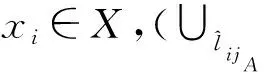
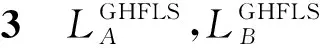
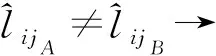
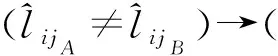
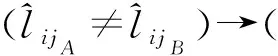
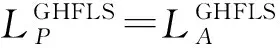
2 广义犹豫模糊语言集的得分函数

2.1 广义犹豫模糊语言集得分函数的定义

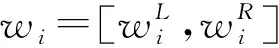
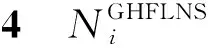
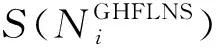
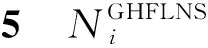
在定义5中，当W未知时，可假设wi=1/m(i∈M)。

定义6LGHFLS的得分函数记为S(LGHFLS)，

定义7LGHFLS的加权得分函数记为SW(LGHFLS)，

定义6是定义7的特殊情况，即W未知时，假设wi=1/m(i∈M)。

本节在探讨GHFLS的得分函数时，始终考虑论域的影响，而不只考虑GHFLNS，具有较严密的数理逻辑。

2.2 广义犹豫模糊语言集得分函数的性质

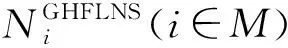
(1)S(LGHFLS)∈[-t′,t′]或者S(LGHFLS)⊆[-t′,t′]。

(2)SW(LGHFLS)∈[-t′,t′]或者SW(LGHFLS)⊆[-t′,t′]。

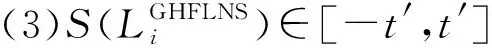
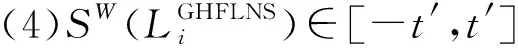
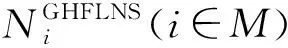
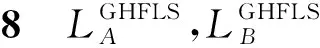
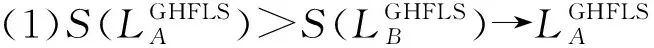
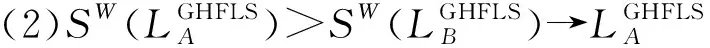
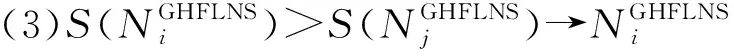
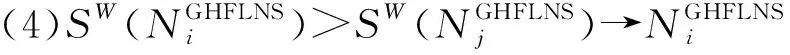
若出现清晰数和区间数混合的情况，则按下述方法处理：

(1)清晰数之间可直接比较大小。

(2)区间数之间可采用可能度排序方法比较大小。

(3)清晰数和区间数之间可利用以下方法比较大小：①判断清晰数是否在区间数界限内；②若不在，则根据清晰数、区间数的上限、区间数的下限比较大小；③若在，则区间数大于清晰数的可能度为(区间数上限-清晰数)/区间数的长度，且区间数小于清晰数的可能度为(清晰数-区间数下限)/区间数的长度。

3 基于得分函数与排序得分的混合多准则群决策方法

3.1 问题描述

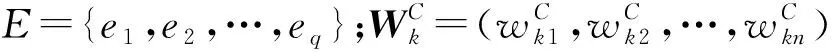
3.2 决策过程

为求解准则权重向量、专家权重向量为清晰数、区间数或未知数且方案赋值为广义犹豫模糊语言集的混合型多准则群决策问题，提出基于得分函数与排序得分的决策方法，具体步骤如下。

步骤1利用定义4，求得ek认为在ai下的S(xkij)，将GHFLDMk转化为GHFLSDM，记为GHFLSDMk=(ykij)m×n，其中ykij=S(xkij)，k∈Q，i∈M，j∈N。

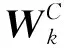
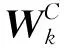
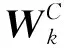
步骤3根据SW(xki)或者S(xki)是否为区间数进行处理：若是区间数，则利用可能度矩阵比较大小；若是清晰数，则直接比较大小(k∈Q，i∈M)。

步骤4根据步骤3的比较结果，确定ek认为ai的排序(k∈Q，i∈M)。

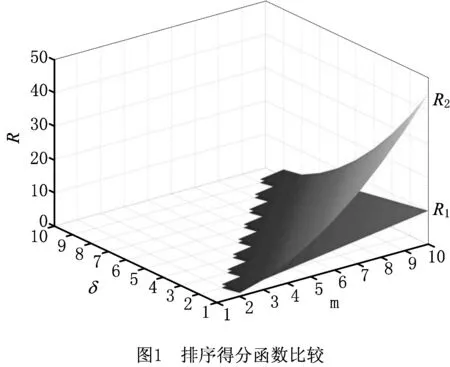
步骤5通常，ek认为ai排在第δki位的排序得分通过Rk(ai)=m-δki+1计算(1≤Rk(ai)≤m，k∈Q，δki,i∈M)[40]，排序得分越高，方案越优；为了拉开排序得分的差距，更好区分方案的优劣，根据模糊Borda法[41]，求得Rk(ai)=(m-δki)·(m-δki+1)/2，(0≤Rk(ai)≤(m-1)·m/2，k∈Q，δki,i∈M)；基于不同的方案个数、排序位置，前述两个公式所求取的排序得分如图1所示，R1表示第1个公式的计算结果，R2表示第2个公式的计算结果，显然，R2的变化幅度与区分性能强于R1。

步骤6根据WE的不同取值情形，计算各个方案的综合排序得分。

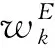
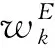
步骤7比较R(ai)的大小，确定ai的最终排序(i∈M)。

4 实例计算与分析

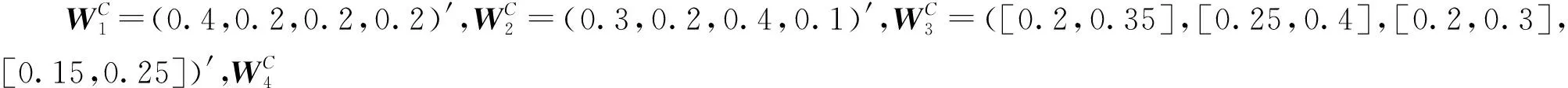
表1 广义犹豫模糊语言决策矩阵GHFLDM1

表2 广义犹豫模糊语言决策矩阵GHFLDM2

表3 广义犹豫模糊语言决策矩阵GHFLDM3

表4 广义犹豫模糊语言决策矩阵GHFLDM4

将以上矩阵转化为GHFLSDMk，求得ek认为ai在C下的SW(xki)或S(xki)(k∈Q={1,2,…,4}，i∈M={1,2,3}，j∈N={1,2,…,4})，如表5所示。

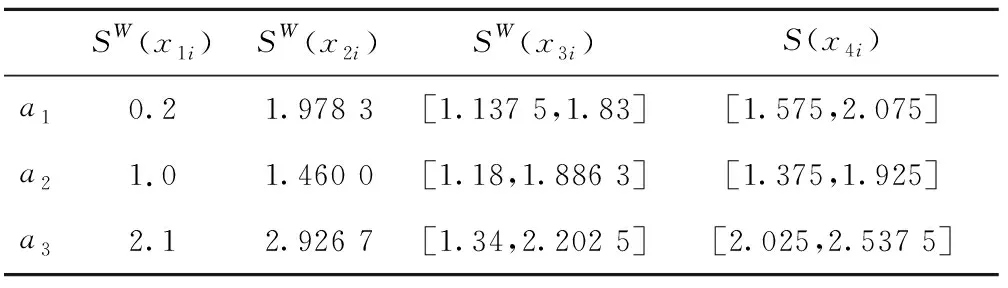
表5 加权得分函数值SW(xki)或得分函数值S(xki)

为了检验方法的可行性和有效性，对本文方法与文献[4-6,8]方法获得的ek算出的ai排序结果进行比较(k∈Q，i∈M)，如表6所示。

表6 排序结果比较

对于每位专家，本文方法得到与文献[4-6,8]方法一致的排序结果，但具有以下优点：能处理不同类型的犹豫模糊语言集，且兼顾各专家给出的不同情形的准则权重向量；得到e3,e4的排序结果均有可能度信息，更利于决策。因此，本文方法更具普适性。

求得ek认为ai排在第δki位的Rk(ai)(0≤Rk(ai)≤3，k∈Q，i∈M)，如表7所示。

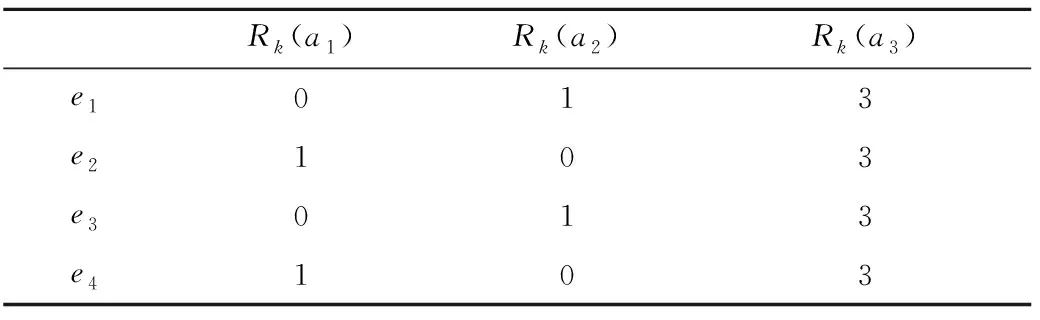
表7 排序得分Rk(ai)

求得ai在C下的R(ai)(i∈M)：R(a1)=0.4，R(a2)=0.6，R(a3)=3.0。

ai的最终排序(i∈M)为a3≻a2≻a1。

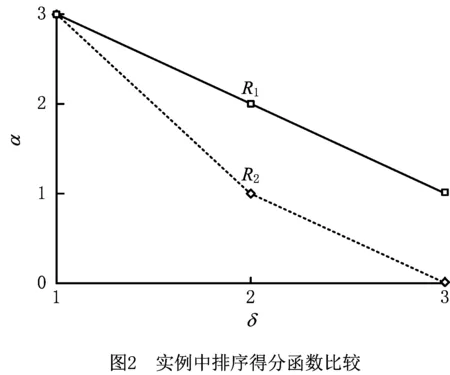
上述计算结果R2和决策步骤5中第一个公式的计算结果R1如图2所示，显然R2对企业信用水平的区分度强于R1。

为更好地对比分析，运用一种常见的多准则群决策方法——逼近于理想解的排序技术(Technique for Order Preference by Similarity to an Ideal Solution, TOPSIS)[42]求解本例，具体步骤如下：

步骤1根据嵌套关系，对每个专家决策矩阵中的各个元素进行线性加权求和→平均→求和→平均，得到信息集结专家决策矩阵。

步骤2对每个信息集结专家决策矩阵求取正理想点ai+和负理想点ai-(i∈M)，如表8所示。

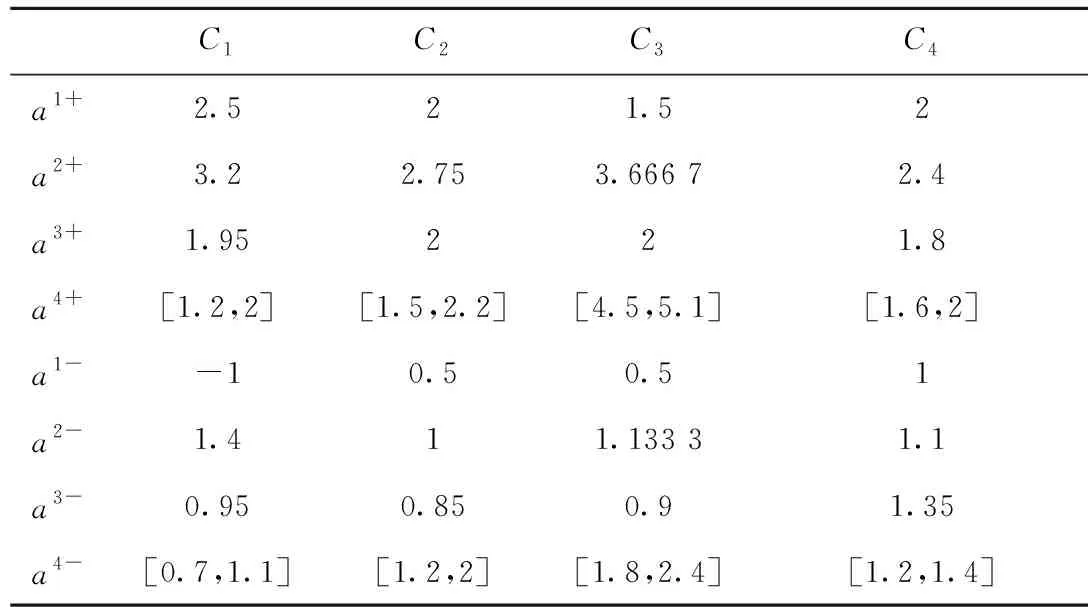
表8 正理想点ai+与负理想点ai-

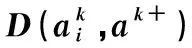
表9 加权距离与

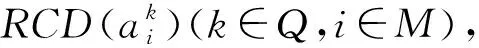
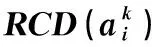
表10 相对接近度

步骤5根据专家权重，计算每个企业的综合相对接近度，记为CRCD(ai)(i∈M)：CRCD(ai)=0.307 1,CRCD(a2)=0.376 3,CRCD(a3)=0.768 2。

步骤6根据综合相对接近度，得到企业的最终排序a3≻a2≻a1。

本文方法与TOPSIS的排序结果一致，但具有以下优点：综合排序得分比综合相对接近度的数值区分度更大；无需求解正理想点、负理想点及加权距离等中间变量，计算步骤清晰、过程简便；区间准则权重向量无需转化为清晰数向量，较好减少了信息损失；区间数排序结果附有可能度信息，更有利于决策。

综上可知，本文方法针对本例决策情形时更具优势。

5 结束语

本文首先统一考虑各类犹豫模糊语言集，定义了GHFLS及其等于、包含于、补、交、并、差、笛卡尔积等运算，然后定义了GHFLS的得分函数并探讨了其性质，进一步提出一种基于得分函数与排序得分的混合多准则群决策方法。最后，应用于新能源汽车零配件小微企业的信用水平综合评估，计算与分析显示该方法具有以下特点：①方案的准则值可为不同类型的犹豫模糊语言集，具有较好的普适性；②准则权重和专家权重可为清晰数、区间数或未知数，且各专家给出的准则权重可不相同；③排序结果稳定性较高，通过可能度信息，可更好支持决策。对于一个犹豫模糊语言决策矩阵中准则值为不同类型的犹豫模糊语言数集的群决策问题，本文方法同样适用，这将在后续研究中探讨。另外，鉴于安相华等[44]考虑准则关联情形，将广义证据推理模型应用于多准则群决策问题中，取得了协同性较好的评价结果，笔者拟在广义犹豫模糊语言多准则群决策的后续研究中考虑准则关联的现实普遍性，并拓展广义证据推理模型的应用范围。