工具约束下多目标拆卸线平衡问题的猫群模拟退火算法

邹宾森，张则强，蔡 宁，朱立夏

(西南交通大学 机械工程学院，四川 成都 610031)

0 引言

资源短缺和环境污染已成为一个全球化问题，制约着人类的进一步发展，而回收再制造是提高资源利用效率以及降低污染的重要途径[1]。拆卸作为再制造中重要的一步，直接决定了产品的循环再生价值、经济效益和环境效应，具有不可估量的作用，但拆卸中任务分配不均会导致拆卸线不平衡，制约拆卸效率的进一步提高。拆卸线平衡问题(Disassembly Line Balancing Problem, DLBP)[2]因其重大的理论意义以及在再制造中广泛的实际应用前景，具有重要的研究价值。

DLBP一经提出便成为了学术界的研究热点。Agrawal等[3]研究了一种U型布局的拆卸线平衡模型，并采用协同蚁群算法进行了求解。Seidi等[4]构建了模糊条件下的拆卸线平衡模型，并用遗传算法进行了求解。丁力平等[5-6]建立了包含最小化闲置率、最大化负荷均衡和最小化拆卸成本的多目标拆卸线平衡模型。针对拆卸中复杂的工况，文献[7-10]研究了不确定环境下的拆卸。已有的DLBP的求解方法包括强化学习算法[11]、变邻域搜索算法[12]等启发式方法[13]和亚启发式方法[14]，上述方法虽结构简单、易于操作，但求解精度不高。目前，遗传算法[15]、人工蜂群算法[16]、粒子群算法[17]、蚁群算法[18]等在DLBP上得到广泛应用，但上述方法均是将多目标问题转化为单目标问题进行求解，丧失了解的多样性。文献[5-6]、文献[19]和文献[20]将Pareto思想与智能算法相结合，分别提出了基于Pareto的蚁群算法、人工鱼群算法和遗传模拟退火算法求解多目标DLBP，一次运算能为决策者提供多种平衡方案，但上述方法的求解质量仍有待进一步提高。

当前DLBP研究中均未考虑拆卸过程中的工具因素以及工具更换对DLBP的影响，而实际拆卸生产中不同类型的拆卸任务需要不同的拆卸工具[21]，频繁更换工具不仅会使实际拆卸作业时间大于理论时间，也会使工人做大量的无用功[22]，工具更换对拆卸线平衡问题有较大影响，同时，考虑工具的更换更加符合实际拆卸工况[21]，因此有必要研究工具约束下的多目标拆卸线平衡问题(Tool Related Constraints Multi-Objective Disassembly Line Balancing Problem, TMDLBP)。

猫群优化(Cat Swarm Optimization, CSO)算法源自猫的生活习性[23]，包含搜寻模式和跟踪模式。近年来，CSO算法的研究应用取得了大量的进展，成功运用于增强通道均衡[24]、提高光伏发电效率[25]和其他多目标问题[26]，表明了CSO算法优良的求解性能。

针对已有DLBP研究中未考虑工具更换对拆卸作业影响的不足，在传统的最大化负荷均衡指标和最小化拆卸成本的基础上，融合工具约束，增加了工具更换指标，建立了TMDLBP数学模型。针对TMDLBP模型特性，设计了一种猫群模拟退火算法，算法可以针对所提问题求得较高质量的Pareto解集。

1 工具约束下多目标拆卸线平衡问题

1.1 问题描述

一个待拆卸产品包含若干个零件，每个零件均不存在损坏或缺失等影响拆卸的情况；每个零件的拆卸工作均在工作站内完成，且一个零件的拆卸任务只能被分配到一个工作站中；若干个拆卸工作站组成拆卸线。零件间不同类型的联接方式需要不同的拆卸工具，同一个工作站内，相邻任务拆卸工具不同，则需要更换工具和考虑更换工具的时间。

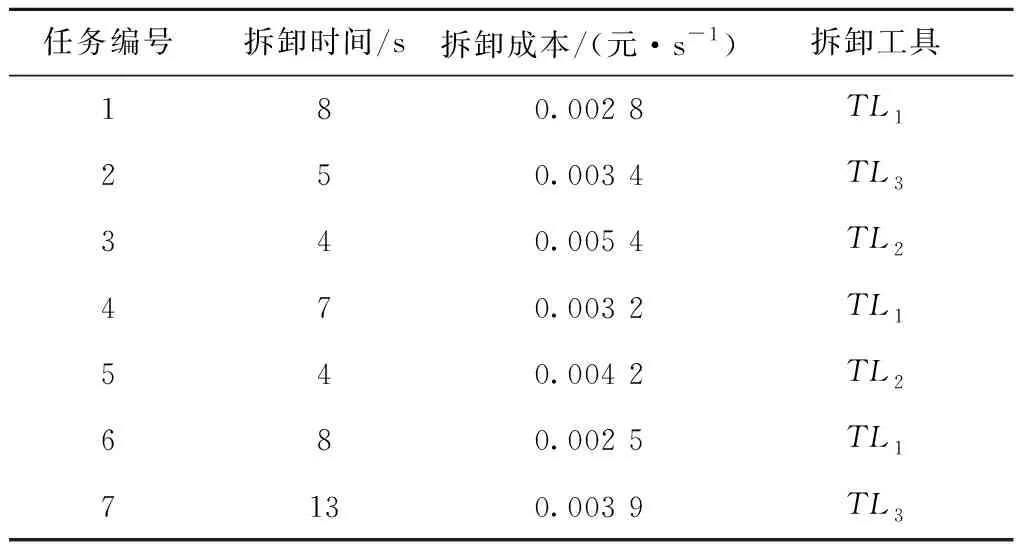
表1 7任务拆卸信息表

包含7个任务的拆卸信息表如表1所示，当拆完任务1紧接着拆任务5时，因两者的拆卸工具不同，则需要更换工具，设定更换一次工具所需时间为Tc，因此实际工作时间为任务1、任务5的拆卸时间与工具更换时间之和。

1.2 数学模型

目标[5]：

(1)

式中:Fsmooth为负荷均衡指标表达式，NWS为开启的工作站数目，j为工作站编号，CT为拆卸线节拍时间，STj为第j个工作站作业时间。拆卸生产中，同一流水线上各个工作站的节拍时间相同，为使每个工作站内分配的任务作业时间尽可能一致、避免分配不均导致的不公平，则应使Fsmooth最大化。

(2)

式中:l为拆卸序列编号，n为零件总数目，ql为拆卸序列中第l处的拆卸任务编号，Rl为工具更换指数，i为拆卸任务编号，xij为任务i与工作站j的分配关系，当任务i被分配到工作站j中则xij=1；否则xij=0。

(3)

式中:rql为任务ql的拆卸工具。当同一工作站内相邻任务拆卸工具不同时，Rl=1；否则Rl=0。

(4)

式中:Fcost为拆卸成本表达式，UTi为任务i的单位时间拆卸成本。拆卸生产中为提高拆卸作业带来的经济收益，在拆卸过程中应尽可能地减小拆卸成本，即最小化拆卸成本Fcost。

(5)

式中Fchange为拆卸线上工具更换总次数。拆卸作业中不同类型的联接方式需要不同的拆卸工具，相邻拆卸任务所使用工具不同时则需要更换工具，为减少拆卸过程中工具更换带来的无用功和导致拆卸生产线效率的降低，应尽可能避免工具的更换，即最小化工具更换次数。

minF=min(1-Fsmooth,Fcost,Fchange)。

(6)

式中F为模型优化目标。

约束条件：

≤NWS≤n。

(7)

式(7)约束开启工作站数目介于最小工作站数和最大工作站数之间。

STj≤CT,∀j∈{1,2,…,NWS}。

(8)

式(8)约束工作站作业总时间不超过节拍CT。

∀i∈{1,2,…,n}。

(9)

式(9)保证每一个零件都被分配到工作站内进行拆卸。

∀aiu=1。

(10)

式(10)确保零件拆卸顺序满足零件优先关系。式中：y为工作站编号，u为拆卸任务编号，aiu为任务优先关系值，当任务i优先于任务u，则aiu=1；否则aiu=0。

2 猫群模拟退火算法

2.1 初始解的产生

TMDLBP的解是满足优先关系的拆卸序列，为保证初始解的随机性和无序性，本文中初始解随机产生。初始解产生过程如图1所示。

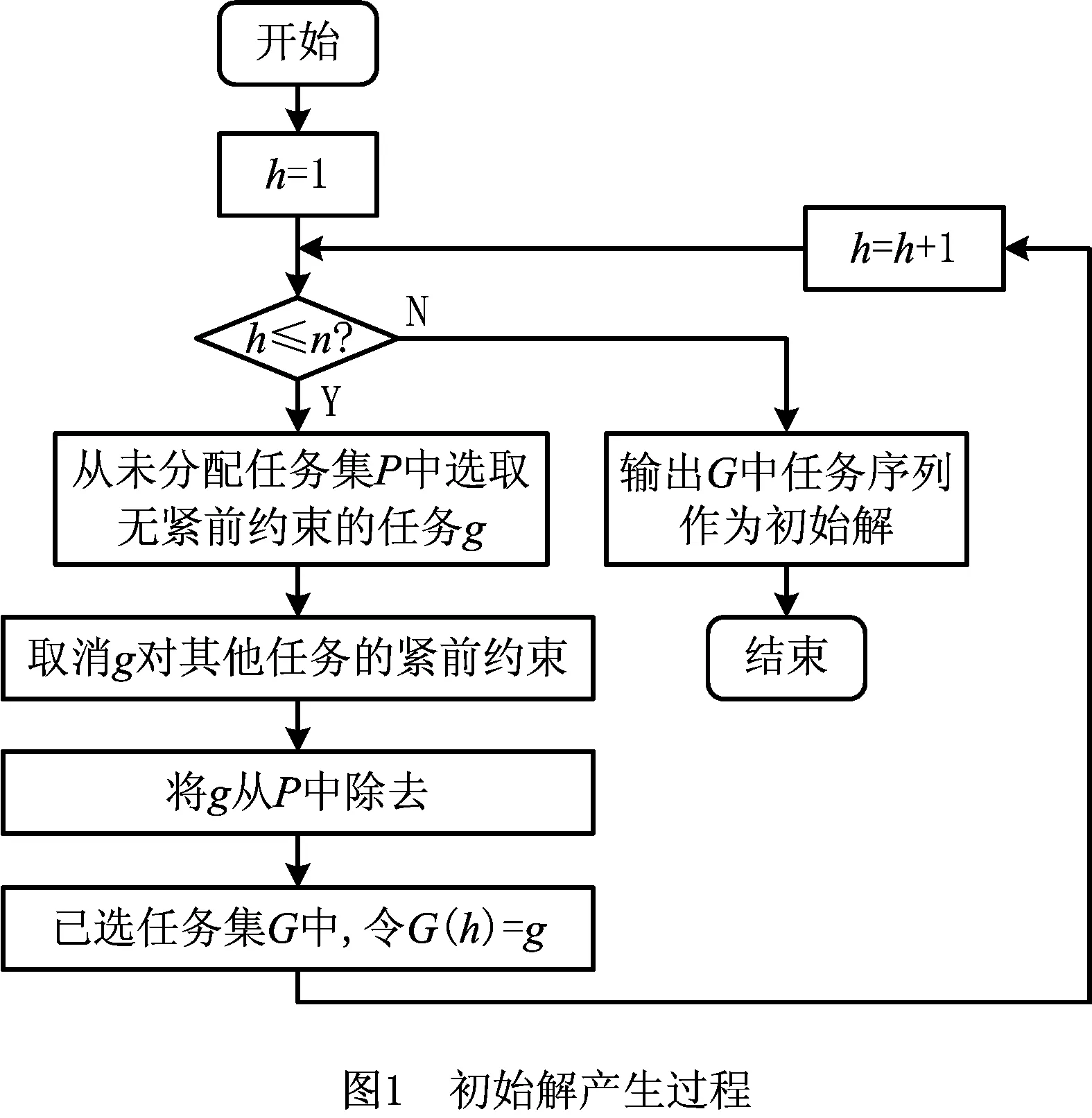
2.2 猫群优化算法

2.2.1 搜寻模式

搜寻模式下，猫将当前位置复制Mnumber份作为副本置于记忆池中，Mnumber为记忆池大小，并在每份副本位置周围进行随机搜索，从记忆池中选取适应度值最高的副本代替当前位置，完成搜寻。针对TMDLBP以拆卸序列为解的编码方式，本文采用基于随机数排序的搜寻模式。搜寻操作示意图如图2所示。

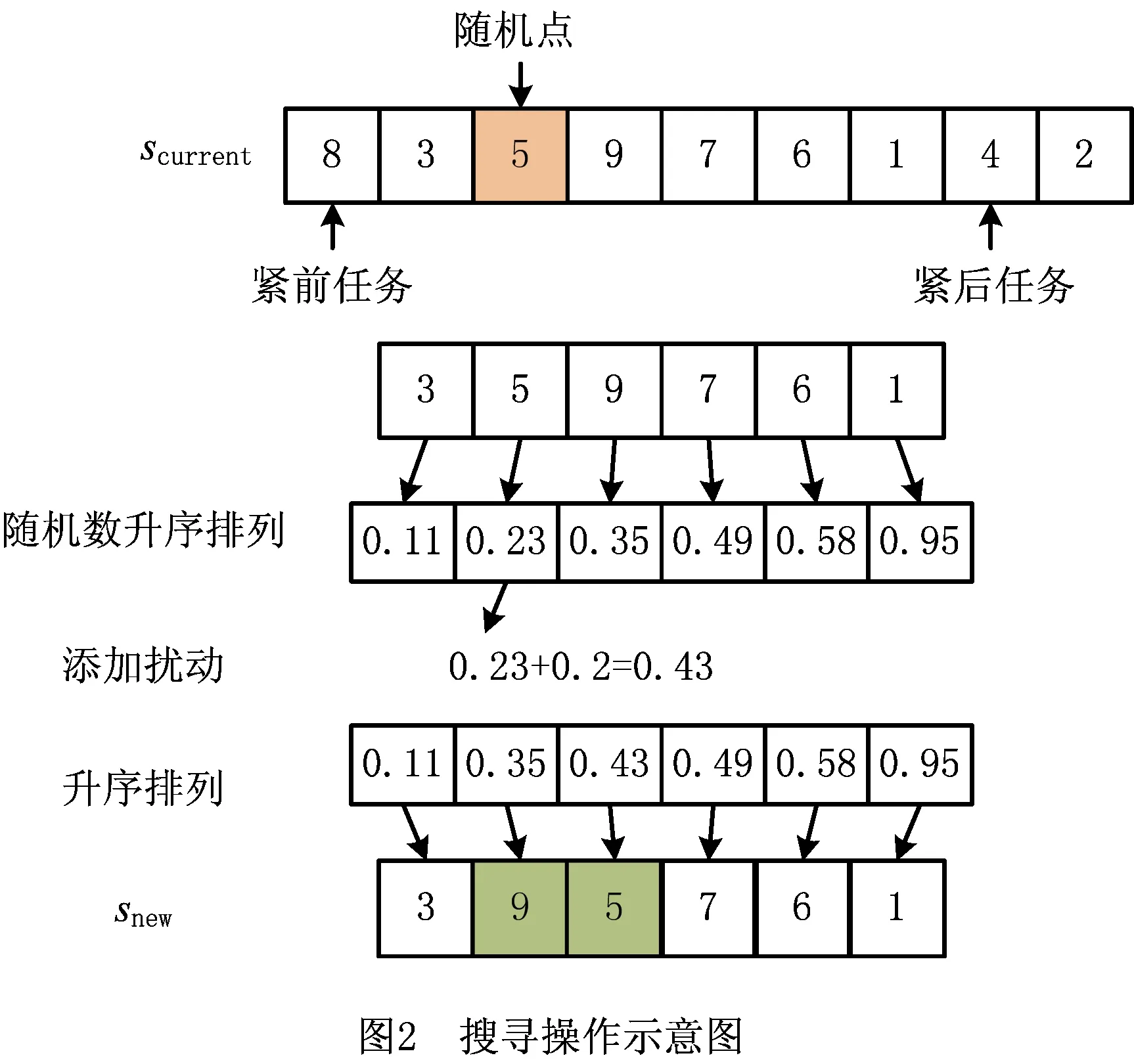
2.2.2 跟踪模式

猫群在跟踪模式下采用式(11)和式(12)所示的速度—位置模型更新当前位置。

(11)

(12)

将式(11)和式(12)合并，则可知：

(13)

拆卸线平衡问题为离散化问题且以拆卸序列作为编码方式，而基本的猫群算法为连续优化算法，因此将猫群算法应用于求解拆卸线平衡问题时需要将算法离散化。基于TMDLBP解的编码特性，定义速度为满足优先关系的对应任务序号的交换，定义位置为拆卸序列。例如vH={(2,3),(8,4)}，含义为将任务2和任务3位置互换、将任务8和任务4位置互换。若XH=[2,8,3,6,1,4,7,5]，则XH+vH=[3,4,2,6,1,8,7,5]。个体位置更新示意图如图3所示。

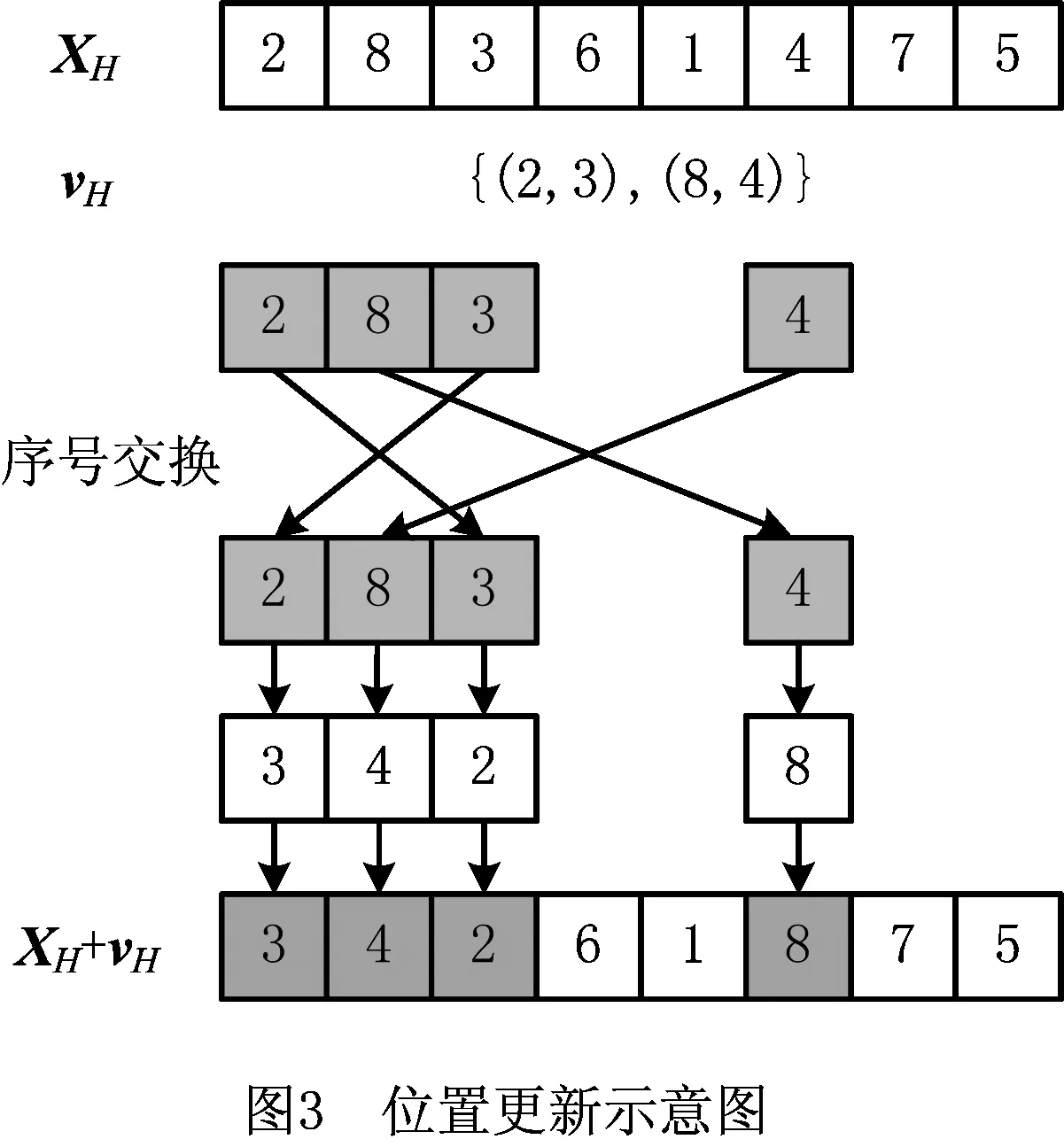
式(13)中，定义位置之差为对应分量的序列的交换，定义c×rand为实际交换位置对数占Le的比例，即实际交换位置对数为c×rand×Le,交换点随机选取。例如Xbest=[2,7,4,1,8,3,5,6]，XH=[3,4,2,6,1,8,7,5]，且任务4优先于任务5，c=0.7，rand=0.47，则实际交换对数为0.7×0.47×8=3对，产生3个随机位置数{2,4, 7}，因则即将XH中7和4位置对换，则XH更新为[3,7,2,6,1,8,4,5]；因则即将XH中1和6位置对换，则XH更新为[3,7,2,1,6,8,4,5]；因则但因任务4优先于任务5，因此该对交换序列不满足优先关系，舍去，故Xbest-XH={(7,4),(1,6)}。图4为个体位置相减操作示意图。

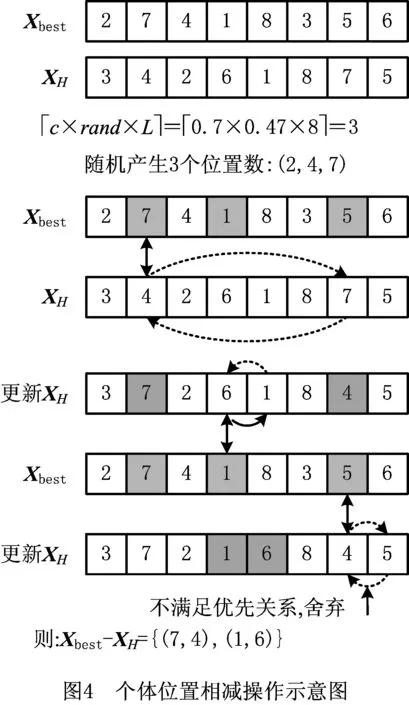
2.3 模拟退火操作

为避免传统CSO算法陷入局部最优，在传统CSO算法的基础上引入模拟退火操作：对完成猫群寻优操作的个体scurrent随机添加一个扰动，使其在当前位置附近局部搜索到达新的位置snew。基于TMDLBP解的编码方式以及任务间优先约束关系的存在，本文采用如下方式进行局部搜索：从当前解scurrent中随机选择一个任务，将该任务随机插入到最近的紧前任务和紧后任务之间，完成局部搜索，形成新解snew。局部搜索示意图如图5所示。

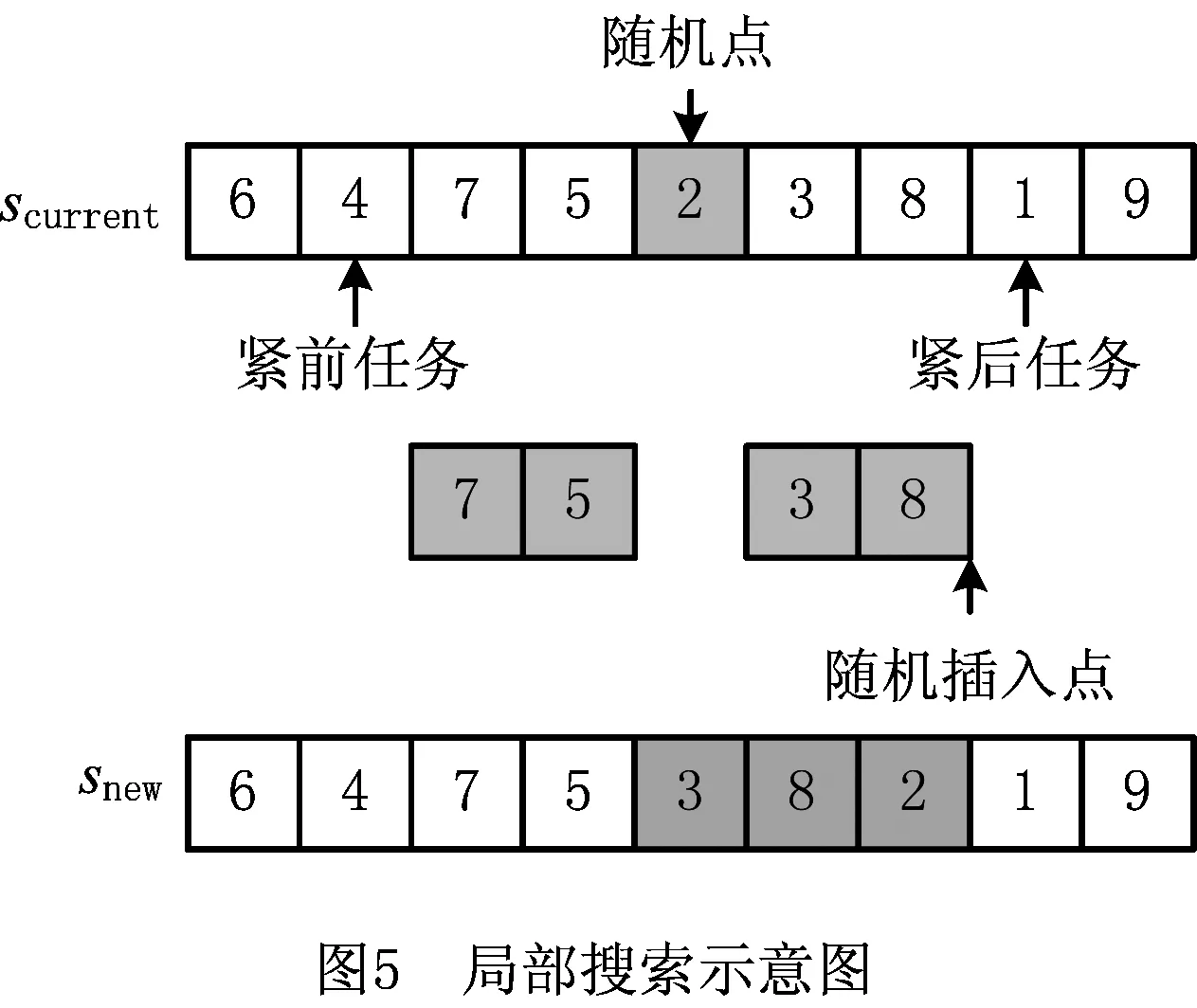
若snew完全优于scurrent，则令scurrent=snew；若snew与scurrent互不占优，则从snew和scurrent中随机选择一个作为当前种群对应个体；若snew劣于scurrent，以一定的概率接受劣解。结合问题特性，采用如下劣解接受准则[27]：

(14)

式中T为当前温度，T=αt×T0，α为降温系数，T0为初始温度，若p>rand，令scurrent=snew；否则scurrent保持不变。

2.4 Pareto非劣解

设多目标问题的可行解s1和s2满足：

∀d∈{1,2},Fd(s1)≤Fd(s2);

(15)

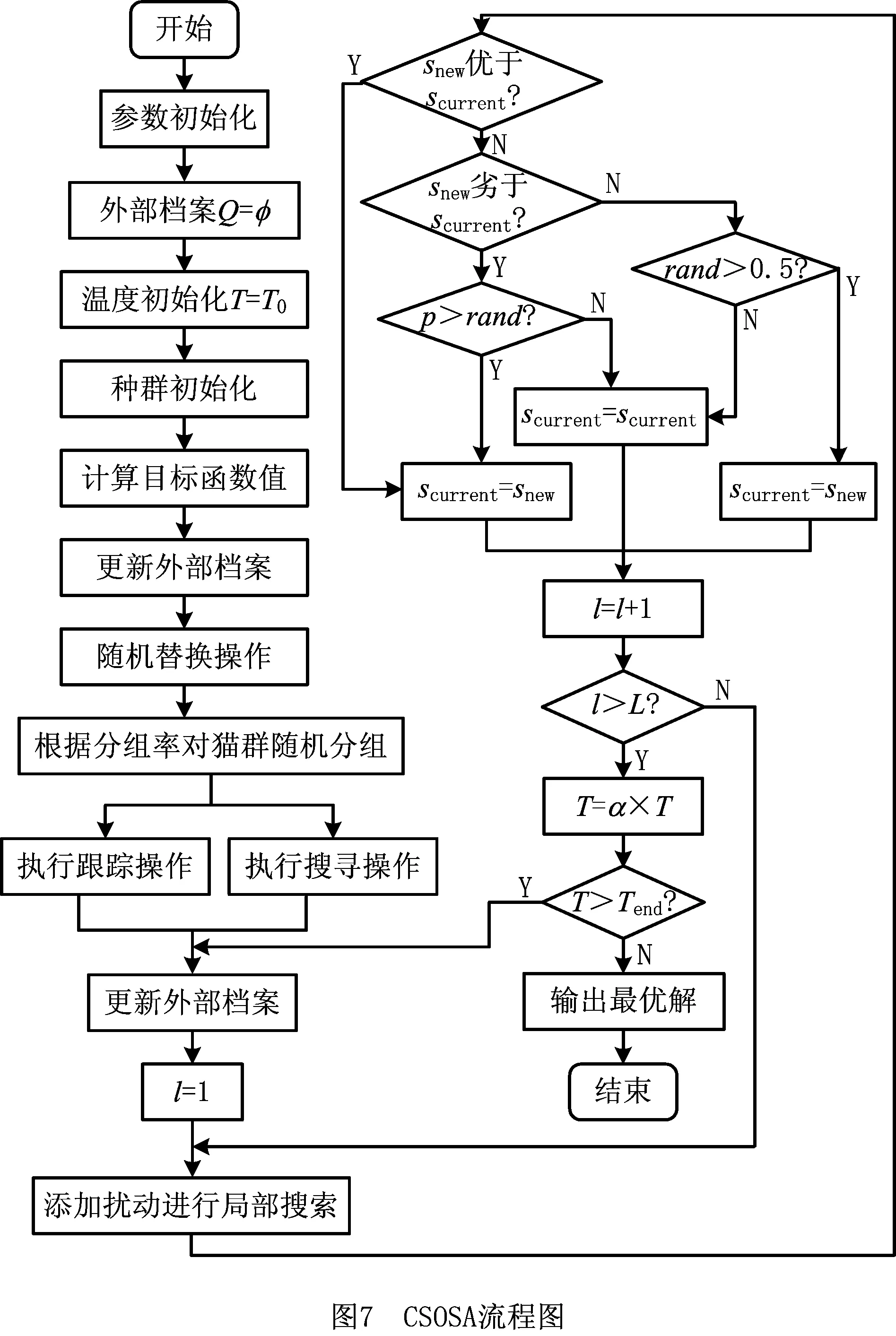
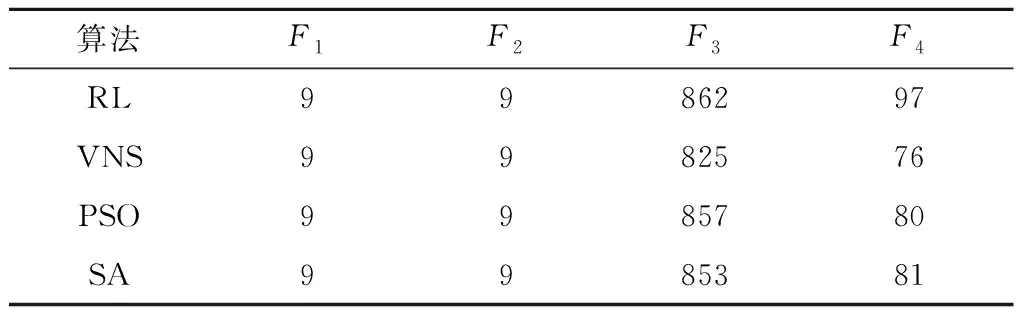
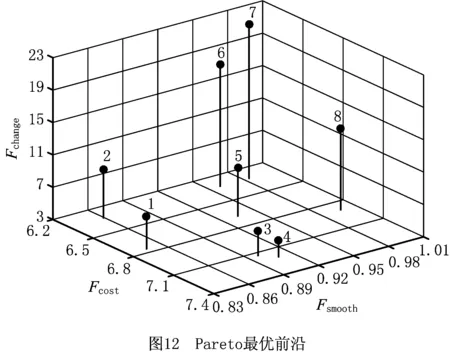
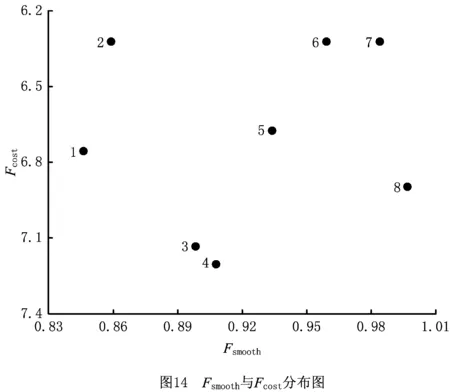
∃d∈{1,2},Fd(s1)

(16)

2.5 外部档案集更新

算法迭代一次完成后，找出外部档案集与当前种群混合集的非劣解集作为新的外部档案集，完成外部档案集的更新。同时采用精英策略，将外部档案集中的种群随机替换掉等同数量的当前种群个体，保证外部档案集中的优秀个体参与到种群迭代循环中，加速算法的收敛。

Pareto非劣解集中的元素规模往往很大，因此应从外部档案集中筛选出具有代表性的子集作为算法输出结果，同时为了使有限的种群尽可能搜索到较多的具有代表性的非劣解，当外部档案集规模过大时需要对外部档案集进行筛选以保证非劣解的多样性。本文采用如下方式对外部档案集进行精简：对目标函数值按升序排列，采用NSGA-Ⅱ机理对每个非劣解进行评价[28]，剔除拥挤距离较小的非劣解，使外部档案集大小等于设定规模，完成外部档案集的筛选。

2.6 算法步骤

猫群算法优化步骤如下：

步骤1算法初始化：种群规模，记忆池大小，分组率，初始温度，降温系数，终止温度，链长，外部档案集规模。

步骤2设定外部档案集为空集。

步骤3温度初始化：令T=T0。

步骤4种群初始化。

财商是一个人判断金钱的敏锐性，以及对怎样才能形成财富的了解。它被越来越多的人认为是实现成功人生的关键。财商和智商、情商一起被教育学家们列入了青少年的“三商”教育。我们从犹太人的财商教育说起，说起犹太人，很多人脑海中想到的第一个国家就是以色列，确实，犹太人的渗透力和生存力非常强，目前，全球经济圈中的很多精英都是犹太人。比如原美联储主席格林斯潘，全球外汇、商品和股票投资家索罗斯，纽约市市长、布隆伯格通讯社创办人布隆伯格……

步骤5计算目标函数值。

步骤6更新外部档案。

步骤7将外部档案集中的个体随机替换当前种群中等同数量的种群个体。

步骤8混合种群，按分组率将种群随机分为搜寻模式和跟踪模式，并分别执行搜寻操作和跟踪操作。

步骤9更新外部档案。

步骤10令l=1。

步骤11对种群个体添加扰动使其到达新位置。

步骤12若snew优于scurrent，则令scurrent=snew，转至步骤16；否则转至步骤13。

步骤13若snew劣于scurrent，转至步骤14；否则转至步骤15。

步骤14若p>rand，令scurrent=snew；否则scurrent保持不变。转至步骤16。

步骤15若rand>0.5，令scurrent=snew；否则scurrent保持不变。

步骤16令l=l+1。

步骤17若l>L，转至步骤18；否则转至步骤11。

步骤18执行降温操作，令T=T×α。

步骤19若当前温度T大于终止温度Tend，转至步骤9；否则执行步骤20。

步骤20输出外部档案集中非劣解集。

步骤21算法终止。

CSOSA流程如图7所示。

3 算法验证与实例应用

为验证算法的有效性以及将本文所提模型和算法推广于实例应用，基于硬件配置为Inter(R)Core(TM)i3-2100 CPU @3.10 GHz，4.00 GB内存的计算机，在Win7系统下采用MATLAB R2014b开发了所提算法的实验程序。

3.1 算法验证

因DLBP的重要研究价值，研究学者结合不同生产情况对DLBP目标模型进行了不断拓展，虽然考虑的目标函数不尽相同，但在求解过程中，只在于解码方式和目标函数值计算的不同，对所采用的求解算法的寻优机制和迭代以及结构不会产生影响，从而不会影响算法的求解性能；同时DLBP模型是TMDLBP模型中工具更换时间为0 s的一种特殊情况，因此采用求解已有DLBP算例来验证所提算法的有效性是可行的。

3.1.1 25规模DLBP算例

文献[11]列出了包含25个拆卸任务的移动电话机拆卸实例(简称P25)的求解信息，其优化目标为：min{工作站数目F1，空闲指标F2，需求指标F3，危害指标F4}。已有的该问题的优化研究均是将多目标问题转换为单目标问题进行求解，求解方法包括强化学习(Reinforcement Learning, RL)算法[11]、变邻域搜索(Variable Neighborhood Search, VNS)[12]、粒子群优化(Particle Swarm Optimization, PSO)算法[17]、模拟退火(Simulated Annealing, SA)算法[29]等，上述4种算法的求解结果如表2所示。

表2 4种算法对P25求解结果

综合考虑所提算法求解性能和该问题求解特性，经不同参数组合下大量运行测试对比后，CSOSA算法参数设置如下：种群规模N=70，记忆池大小Mnumber=7，分组率Grate=0.1，常数c=0.8，初始温度T0=100，降温系数α=0.98，终止温度Tend=0.05，链长L=6，外部档案规模fnumber=7。算法程序运行30次，取其中一次运行结果所求得的7个平衡方案如图8所示。

对比分析表2和图8数据，RL、PSO和SA求解结果中：F1、F2指标均为9，与方案1和方案2对应指标相同；F3指标最小值为853、F4指标最小值为80，分别劣于方案1和方案2，因此可知上述3种算法求解结果劣于方案a和方案b。RL、PSO和SA求解结果与方案3～方案7互不占优，即本文所提CSOSA求解结果中，既有优于上述3种算法求解结果的方案，也有与上述3种算法求解结果互不占优的方案，但没有劣于上述3种算法求解结果的方案，因此可知，本文所提算法优于上述3种算法。

VNS求解结果与本文所求方案2相同，与另6种方案互不占优。但本文所求得的7组方案中，方案1、方案6、方案7的F3指标分别为823、807、802，优于VNS求得的F3指标825；方案3～方案7的F4指标分别为73、72、70、72、72，优于VNS求得的F4指标76。当决策者注重F3指标时，可以选择F3指标为802的方案7；当决策者注重F4指标时，可以选择F4指标为70的方案5。即相比文献[12]，本文引入了Pareto思想并在求解过程中存储了全局非劣解集，能求得分布范围更广、多样性更丰富的方案，能为决策者提供更多的选择，因此可知本文求解质量优于文献[12]所提VNS。

由上述对比分析可知本文所提CSOSA算法优于上述4种算法，同时，相对通过赋予权重将多目标问题转化为单目标求解的不足，本文所提CSOSA一次运算能求得多组平衡方案，且在各个指标上均能取得较好的分布，能为决策者提供更多的决策方案，验证了所提算法在DLBP求解中的有效性和高效性。

3.1.2 52规模DLBP算例

文献[5]、文献[19]和文献[20]分别采用蚁群优化(Ant Colony Optimization, ACO)算法、人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA)和遗传模拟退火(Genetic Simulated Annealing, GSA)算法求解了包含52个任务的DLBP(简称P52)，其求解目标为最小化闲置率Fidle、最大化符合均衡指标Fsmooth、最小化拆卸成本Fcost，其中：

(17)

综合算例特性和算法结构，算法参数设置如下：种群规模N=80，记忆池大小Mnumber=7，分组率Grate=0.15，常数c=0.7，初始温度T0=500，降温系数α=0.97，终止温度Tend=0.4，链长L=5，外部档案规模fnumber=7。算法程序运行30次，取其中一次运行结果如表3所示、Fidle和Fcost对比图如图9所示。

表3 P52拆卸方案

表3中方案编号与图9中方案编号一一对应。上述三种算法在Fidle指标上所求得的值均相同，因此Fidle指标不影响对比结果。对三种算法所求得方案的Fsmooth指标和Fcost指标取平均值进行对比：CSOSA、AFSA和GSA在Fsmooth指标上所求得的均值分别为0.984 2、0.984 9和0.992 3；在Fcost指标上所求得的均值分别为133.625、138.740和137.558。由此可知在Fsmooth指标均值对比中，CSOSA劣于AFSA和GSA，但在Fcost指标均值对比上，CSOSA优于AFSA和GSA。因此通过取均值方式对比可知3种算法求解结果互不占优，但CSOSA在Fsmooth指标和Fcost指标上均能求得比AFSA和GSA求解结果更优的0.998 5和128.718，能为决策者在这两个指标上提供更好的选择。

图9中带标号的方案分别为图中对应算法求解的方案。对CSOSA和AFSA求解结果进行逐一对比分析，方案1与方案8～方案15互不占优；方案2完全优于方案8，与其余7组方案互不占优；方案3完全优于方案8～方案10，与方案11～方案15互不占优；方案4优于方案8～方案12，与方案13～方案15互不占优；方案5优于方案10～方案14，与方案8、方案9、方案15互不占优；方案6优于方案13～方案15，与方案18～方案12互不占优，且方案6的Fsmooth指标0.998 1优于AFSA所求得的所有Fsmooth指标；方案7优于方案15，与方案8～方案14互不占优。即可知，CSOSA求得的部分方案优于AFSA所求得的部分方案，没有完全劣于AFSA的方案，且CSOSA能求得更优的Fsmooth指标和Fcost指标，能为拆卸作业提供更加优良的选择；但AFSA所求得的方案中，没有一组方案优于CSOSA所求得的方案，因此可知通过对方案的逐一对比，CSOSA在DLBP求解中优于AFSA，验证了CSOSA算法的有效性。

由图9可知，方案1～方案3与方案16～方案25互不占优；方案4完全优于方案16～方案20、与方案21～方案25互不占优；方案5完全优于方案16～方案24、与方案25互不占优；方案6优于方案24和方案25、与方案16～方案23互不占优；方案7与方案16～25互不占优。但GSA求解结果中没有方案完全优于CSOSA求解结果中的任何一组，因此可知本文所提CSOSA优于文献[20]所提GSA，且本文所提CSOSA能求得更低的拆卸成本128.178、128.268、129.006、129.096、130.740，相对文献[20]能为决策者提供更低成本的拆卸方案以提升拆卸效益。

3.2 实例应用

为分析本文所提模型实际应用情况，以及进一步验证CSOSA算法的实用性，将所提模型和算法应用于某型号打印机拆卸生产线。该打印机主要包含55个零部件，零部件名称及编号如图10所示。

综合考虑该打印机的结构和零部件拆卸位置，分析零件拆卸过程中的约束和干扰，制定了如图11所示的零部件拆卸优先关系图，箭头表示零件之间的优先关系：箭头末端的任务必须在箭头始端的任务拆卸完成之后才能进行拆卸。

经多次秒表测量取平均拆卸时间，得到表4中各零部件拆卸时间；经统计，该型号打印机拆卸过程中工具有4种，为方便表述，将其分别标号TL1～TL4。表4中拆卸成本经结合市场情况、工厂作业固定成本以及工人劳力成本统计而来。给定拆卸工作站节拍CT=58 s、工具更换一次时间TC=4 s。

表4 包含55个任务的打印机拆卸信息表

兼顾算法求解时间与求解效果，经大量测试不同参数组合后，算法参数设置如下：种群规模N=90，记忆池大小Mnumber=10，分组率Grate=0.15，常数c=0.9，初始温度T0=90，降温系数α=0.98，终止温度Tend=0.1，链长L=5，外部档案规模fnumber=8。程序运行30次，取其中一次求解结果如表5所示，所求方案Pareto最优前沿如图12所示、Fsmooth与Fchange分布图如图13所示、Fsmooth与Fchange分布图如图14所示。

表5 P55拆卸方案

以方案1为例简述工具更换指标：任务42、任务32、任务37、任务29、任务48、任务55、任务53在各自所在工作站内与各自的上一任务所用拆卸工具不同，均需要更换一次拆卸工具；其余工作站中每个工作站均只需使用一种工具，因此无需更换工具。本文所建立模型考虑了工具更换指标，在算法求解优化过程中，工具更换次数更少的方案会被保留在外部档案中，因此求解结果能为决策者提供更低工具更换次数的方案。

由表5可知，针对该型号打印机拆卸线，所提算法一次求得的平衡方案的负荷均衡指标Fsmooth的范围为0.846 3～0.996 9、拆卸成本Fsmooth的范围为6.322 0～7.203 6、工具更换次数Fchange的范围为5～22。由图13～图15可知，所提算法求得的Pareto非劣解集分布较为广泛：当决策者注重负荷均衡指标Fsmooth时，可以选择Fsmooth指标为0.996 9的方案8；当决策者欲降低拆卸成本Fcost时，可以选择方案2、方案6、方案7中的任意一种方案；当决策者欲减少工人无用功、使拆卸线中工具更换次数最小时，可以选择方案4；当决策者综合决策时，可以从方案1～方案8中任意选择一种平衡方案作为实际执行方案。单个产品拆卸时不同方案在某个目标值上差距可能较小，但因拆卸线流水化大规模作业，该差距因素会被放大，因此对拆卸方案进行择优选用。

4 结束语

本文提出了涉及拆卸工具类型及考虑拆卸工具更换对拆卸生产作业影响的多目标拆卸线平衡问题，将拆卸工具更换的时间计入拆卸作业时间，在负荷均衡指标、拆卸成本指标的基础上增加工具更换指标，建立了工具约束下的多目标拆卸线平衡问题数学模型，并设计了一种基于Pareto的多目标CSOSA算法对模型进行求解。针对TMDLBP问题特性和编码方式，提出了基于序列交换的离散跟踪模式；为提高算法的全局搜索能力，引入拥挤距离筛选外部档案和模拟退火机制。经对25规模和52规模算例求解并与其他算法求解结果对比分析，验证了所提CSOSA良好的全局寻优能力。将所提模型和算法应用于55规模的某型号打印机拆卸线设计中，考虑拆卸工具更换时间的拆卸方案更加符合实际生产情况，且求解结果能为决策者提供多样化的决策空间。

本文对考虑工具更换的多目标拆卸线平衡问题以及猫群模拟退火算法展开了研究，所提模型更加符合实际生产工况，同时拓宽了DLBP求解方法。本文所提模型是基于所有零件均为完好的理想的状态，而回收产品中可能存在零件缺失、损坏不易拆卸的情况，下一步拟研究考虑零件不确定性的多目标拆卸线平衡问题。