钢纤维煤矸石混凝土冻融后本构关系试验研究

邱继生，王民煌，关 虓，潘 杜，郑娟娟，张程华

(西安科技大学 建筑与土木工程学院，陕西 西安 710054)

0 引 言

煤矸石是在煤炭形成过程中与煤伴、共生的一类岩石的混合物。其热值较低，成分复杂，难以利用，在煤炭开采加工过程中通常成为工业废弃物。煤矸石约占煤产量的10%～15%左右，约占全国工业固体废弃物总量的40%，我国煤矸石已累计堆存50亿吨以上，且随着我国煤炭产量的持续增加而逐年剧增[1-3]。若无合理的利用，废弃、堆积的煤矸石将会严重污染环境，特别是硫化物和重金属的污染，将会产生巨大的社会、经济损失，同时煤矸石堆积成的矸石山本身也有自燃、滑坡等安全隐患。故而有效、合理利用的利用煤矸石，无疑是诸多国内外煤矿工作者和相关领域研究者们努力的方向。目前比较常见的煤矸石利用方法包括：利用煤矸石燃烧发电、分选矿物作为化工原料以及将煤矸石作为建筑材料。其中，煤矸石作为建筑材料方面，国外已有不少将煤矸石用作工程填充物或水泥替代物的工程实践[4，5]，国内也已有许多关于煤矸石利用的研究成果[6-8]，但煤矸石混凝土的应用仍受到一定的限制，其中最主要的原因是高取代率(30%以上)的煤矸石混凝土的抗冻性能难以满足规范要求[9-11]。另一方面，通过掺入钢纤维增强混凝土是混凝土改性的一种重要手段。为了克服混凝土本身抗拉强度低、易于开裂等缺陷，在混凝土中掺入一定均匀乱向分布的短钢纤维以改善其性能。前人众多的研究结果表明：乱向分布的短钢纤维掺入混凝土中，能够有效地改善混凝土内部孔结构，同时阻碍混凝土内部微裂缝的扩展和宏观裂缝的形成，能够有效提升混凝土的抗拉、抗弯、抗冲击、抗疲劳及抗冻性能[12-19]。故考虑通过在高取代率的煤矸石混凝土中掺入乱向分布的短钢纤维以改善其抗冻性能，从而可以进一步推广应用煤矸石混凝土这一绿色建筑材料。但目前针对钢纤维煤矸石混凝土的相关研究较少，并且尚未有一个被广泛认可的钢纤维煤矸石混凝土冻融后单轴受压本构模型，难以进一步研究钢纤维对煤矸石混凝土的力学性能和抗冻性能的影响。针对该问题，文中通过冻融后的钢纤维煤矸石的单轴受压试验，探讨了钢纤维掺量和冻融循环次数与冻融后钢纤维煤矸石混凝土的应力-应变曲线间的关系，为进一步分析钢纤维煤矸石混凝土的力学性能和推广应用煤矸石混凝土提供依据。

1 试验材料和试验方法

1.1 试验材料

水泥用陕西秦岭股份有限公司P·O42.5R普通硅酸盐水泥；砂用级配合格的河砂，细度模数2.7，堆积密度1 460 kg/m3；碎石用普通碎石，粒径5～16 mm，混合级配；煤矸石用陕西某煤矿所产的煤矸石，粒径5～20 mm，混合级配；钢纤维用波浪型短钢纤维，长25～30 mm，等效直径0.5 mm.

1.2 试件制作及配合比

用煤矸石等体积代替40%的碎石，并掺入钢纤维，为保证钢纤维乱向分布并防止结团，拌合时先干拌后湿拌。参考GB/T50080-2002《普通混凝土拌合物性能试验方法标准》和 GB/T50081-2002《普通混凝土力学性能试验方法标准》的规定，共成型试件4组，钢纤维掺量分别为0%，0.5%，1%和1.5%，每组20个试件，尺寸皆为100 mm×100 mm×300 mm，各组编号及其配合比见表1.试件浇筑后24 h脱模，送入标准养护环境养护28 d.

1.3 试验方法与试验装置

试件养护完成后，根据GB/T50082-2009《普通混凝土长期性能和耐久性能试验方法标准》以快冻法进行冻融试验。试验装置为北京数智意隆仪器有限公司生产的KDR-V9系列混凝土快速冻融试验机。一次冻融循环冻结完成时试件中心温度-17±2 ℃，降温时间1.5～2.5 h，融化完成时试件中心温度8±2 ℃，升温时间1.0～1.5 h，冻融过程中试件中心与表面的温差始终<28 ℃.

表1 钢纤维煤矸石混凝土配合比

根据试验方案，冻融达到一定循环次数时进行质量和动弹性模量的测量。动弹性模量的测量仪器为北京康科瑞有限公司生产的NM-4B型非金属超声检测分析仪，接收灵敏度≤10 μV，测量精度±0.1 μs；质量的测量仪器为常熟市天量仪器有限责任公司生产的LT20K型工业计重天平，分度值0.001 kg.测量完成后取出达到预期冻融循环次数的试件，其余继续冻融。

待试件达到预期循环次数后对其进行单轴受压试验。试验装置为上海华龙测试仪器有限公司生产的WAW-1000型微机控制电液伺服万能试验机，加载速度0.5 mm/min.位移采用电子位移计测量，标距100 mm，分度值0.001 mm.

2 试验结果分析

2.1 冻融损伤

各组试件随着经历冻融循环次数的增加，表面砂浆体出现剥离、细骨料和钢纤维脱落的程度也逐渐加剧，经历不同冻融次数的试件表面特征如图1所示。

图1 不同冻融次数下表面特征对比Fig.1 Surface Comparison in different freeze-thaw cycles

混凝土整体冻融损伤的程度仅通过观察难以全面客观的定量评价，而相对质量损失MXS和相对动弹性模量损失E(t)XS被普遍认为是评价冻融损伤程度的有效指标。图2给出了经历30次冻融循环后，不同钢纤维掺量的各组试件的相对质量损失和相对动弹性模量损失。

图2 冻融损伤情况Fig.2 Freeze-thaw damage

图2表明，各组试件相对动弹性模量损失无显著区别，而掺入钢纤维会使相对质量损失增大。根据现有的研究成果[16-19]，并结合本次试验，说明掺入钢纤维对限制煤矸石混凝土表面材料的剥落作用不大，甚至由于边界效应，当钢纤维表面与胶凝材料结合质量不好时其表面较之砂浆体或细骨料更易剥落，从而导致质量损失较大。此外，通过项目相关的毛细吸水试验表明，由于相对质量损伤是在吸水饱和状态下测量得到的，普通煤矸石混凝土饱和吸水质量增加较多使其质量损失较小，因此掺入钢纤维对减小煤矸石混凝土的质量损失和提高动弹性模量作用不明显。

2.2 应力-应变曲线及其主要参数

F0组和F15组试件经历不同次数冻融后，通过单轴受压试验得到的应力-应变曲线如图3和图4所示。

各组试件未经冻融和经30次冻融后，通过单轴受压试验得到的应力-应变曲线如图5和图6所示。

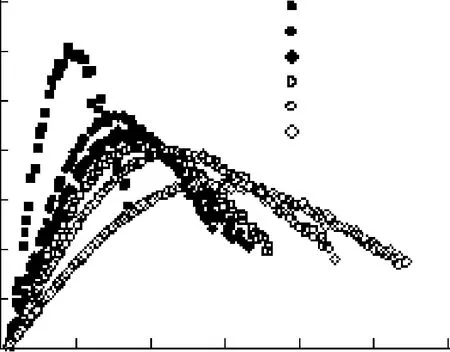
图3 F0组应力-应变曲线Fig.3 Stress-strain curve of the F0 team

图4 F15组应力-应变曲线Fig.4 Stress-strain curve of the F15 team

随着循环次数的增加，F0组和F15组试件峰值应力降低，峰值应变增加，应力-应变曲线趋于扁平，同时初始切线模量和峰值点割线模量同时降低。这是由于冻融作用使混凝土内部出现损伤，这些损伤会随冻融循环次数的增加而积累，在混凝土内部形成大量的微孔洞和微裂缝，使其内部结构逐渐疏松，一方面导致混凝土强度下降，另一方面导致混凝土出现压实效应，刚度下降，应变增加。

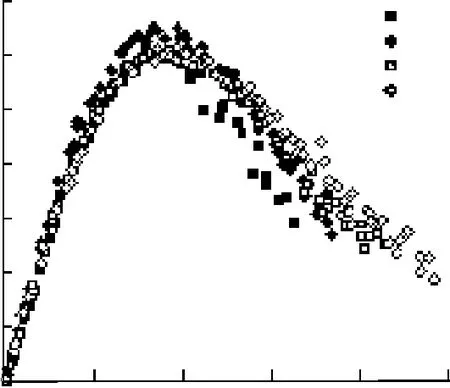
图5 未经冻融时应力-应变曲线Fig.5 Stress-strain curve without freeze-thaw cycles

图6 经历30次冻融后的应力-应变曲线Fig.6 Stress-strain curve after 30 freeze-thaw cycles

随着纤维掺量的增加，各组试件表现出两点较显著的区别，其峰值应变增加，以及下降段的下降速度减缓。这是由于在受压初期，钢纤维对煤矸石混凝土受力性能影响较小，而在接近峰值和之后的下降段中，钢纤维能有效阻碍煤矸石混凝土内部裂缝发展，提供约束，使应力-应变曲线表现出较为较显著的区别。

3 本构方程的建立

已有众多学者提出了多种混凝土受压应力-应变全曲线方程[20-25]，文中参照文献[20]中的混凝土应力-应变曲线方程

(1)

式中σ为应力；E为荷载损伤为0时的弹性模量，即只有冻融损伤的混凝土的弹性模量，简称为弹性模量；ε为应变，单位为1/1 000；m为曲线参数；εpk为峰值应变。现根据试验结果分别确定各参数的取值方法。

3.1 弹性模量E的确定

文中取应力为40%峰值应力时的割线模量为弹性模量E，低应力状态下钢纤维对整体受力性能影响较小，冻融损伤的累积和微裂缝的扩展导致的酥松对混凝土试块的变形有较大影响从而也影响了弹性模量的大小，试验数据表明不同钢纤维掺量的试件的弹性模量随冻融循环次数的变化趋势也基本一致。

故只考虑冻融循环次数对弹性模量的影响，拟合试验数据，得到弹性模量与冻融循环次数之间的关系如下

E=34 400exp(-0.037N)

(2)

式中N为冻融循环次数。试验数据与拟合曲线的关系如图7所示。

图7 弹性模量的试验数据与拟合曲线Fig.7 Test data and fit curves of elastic modulus

3.2 峰值应变εpk的确定

试验研究表明，不同钢纤维掺量的试件，其相对峰值应变随冻融循环次数变化的规律基本相同。故先考虑冻融循环次数对相对峰值应变的影响，拟合试验数据，得到二者之间的关系如下

(3)

式中ε0为未经历冻融时的峰值应变。

各组试件的相对峰值应变随冻融循环次数的变化规律如图8所示。

图8 相对峰值应变的试验数据与拟合曲线Fig.8 Test data and fit curves of relative peak strain

进一步考虑钢纤维掺量对峰值应变的影响，未经历冻融时的试件的峰值应变如图9所示。

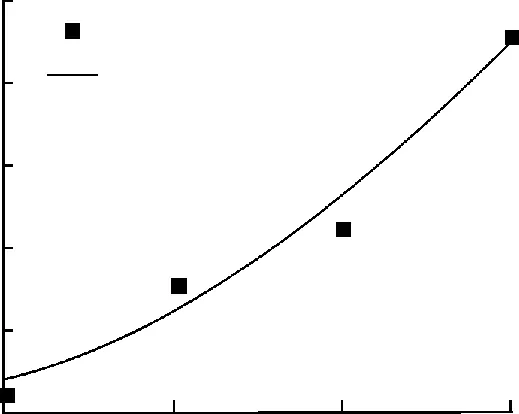
图9 冻融前的峰值应变拟合Fig.9 Fit of peak strain before freeze-thaw cycles

拟合试验数据得到

ε0=(1.67+0.054 8S+0.056S2)

(4)

式中S为钢纤维掺量，单位为1/100.

将式(4)带入式(3)得到峰值应变的计算公式

εpk=(1.67+0.054 8S+0.056S2)exp(0.021 88N)

(5)

3.3 参数m的确定

将式(2)、式(5)带入式(1)，并根据试验数据拟合确定参数m的取值，每组绘制柱状图如图10所示。

图10 m值对比Fig.10 Comparison of the value of m

试验发现同一组不同冻融循环次数下试件的m值相差不大，考虑m值只受钢纤维掺量影响，取钢纤维掺量相同的所有试件的m值的平均值作为该钢纤维掺量的混凝土的m值，结果如图11所示。

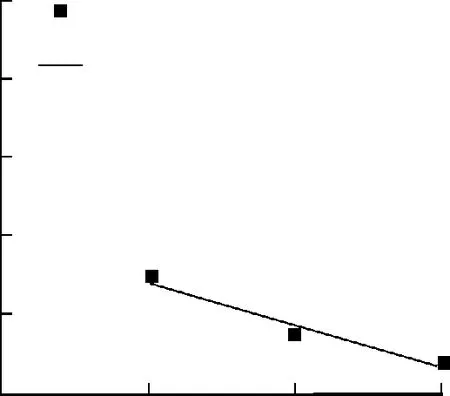
图11 各组试件的m值与拟合曲线Fig.11 Value and fit curves of m of each group specimens

由图11所示，对钢纤维掺量在0.5到1.5之间的钢纤维煤矸石混凝土拟合建立m值与钢纤维掺量之间的关系为

(6)

3.4 验证

通过式(2)、式(5)和式(6)分别求出E，εpk和m，并带入式(1)，即可绘出经历了一定冻融循环的一定钢纤维掺量的煤矸石取代率为40%的钢纤维煤矸石混凝土的应力-应变曲线。

根据式(1)，峰值应力应满足

σpk=Eεpk/exp(1/m)

(7)

式中σpk为峰值应力，即强度。

试验数据与式(7)的预测曲线如图12所示。

图12 强度的试验数据与预测曲线Fig.12 Test data and forecast curves of strength

图12反应出此本构关系对未经冻融的试件的强度预测较差，但此时试件的强度易由其他方法测出，此本构关系能较好的反应出钢纤维煤矸石混凝土冻融后单轴受压的力学性能，且误差基本偏于安全。

故取经历30次冻融循环后，不同钢纤维掺量的各组试件的实测应力-应变关系和采用式(2)、式(5)、式(6)和式(1)绘出的理论应力-应变全曲线对比图如图13所示。

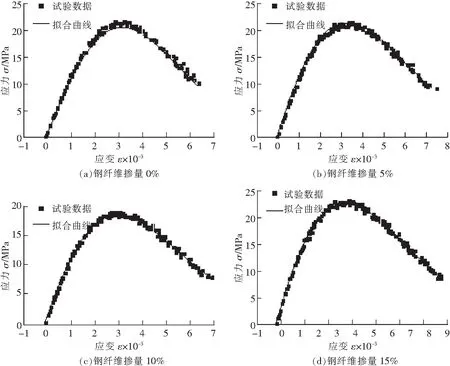
图13 应力-应变的试验数据与理论曲线Fig.13 Test data and theoretical curves of stress-strain

图13表明，在适当的钢纤维掺量和经历一定的冻融循环的情况下，文中给出的本构关系能较有效的描述钢纤维煤矸石混凝土的应力-应变关系，对工程分析和进一步研究有一定的参考价值。

4 结 论

1)随着冻融循环次数的增加，应力-应变全曲线的峰值应力降低，峰值应变增加，弹性模量降低，应力-应变曲线趋于扁平；

2)掺入钢纤维不能显著降低煤矸石混凝土的冻融损伤，但能使煤矸石混凝土峰值应变显著增加，对峰值应力和弹性模量基本没有影响，可考虑加入引气剂进一步改善其抗冻性；

3)钢纤维煤矸石混凝土不宜直接用于严寒地区，但对寒冷地区和夏热冬冷地区而言，其力学性能和耐久性能都已满足工程需求；

4)对经历了一定冻融循环的一定钢纤维掺量的煤矸石取代率为40%的钢纤维煤矸石混凝土，可由文中方法得到其单轴受压时的本构关系。