有学习的高阶DPA攻击

吴震，王燚，周冠豪,2



有学习的高阶DPA攻击

吴震1，王燚1，周冠豪1,2

（1. 成都信息工程大学网络空间安全学院，四川 成都 610225；2. 北京智慧云测设备技术有限公司，北京 102300）

在侧信道攻击中，作为抵抗一阶DPA攻击的对策，掩码策略是当前使用最为广泛的防御方式之一。目前，针对掩码策略，通常使用高阶DPA及高阶模板攻击等攻击方式。但由于高阶DPA攻击的是多种信息的联合泄露，需要对多个位置的能耗进行交叉组合，导致其攻击效率低下。高阶模板攻击则需要在学习阶段了解每次加密中使用的随机掩码，攻击条件往往难以满足。针对目前这些攻击方式的不足与局限性，有学习的高阶DPA采用神经网络建立能耗对无掩中间组合值的拟合模型，基于拟合无掩中间组合值与猜测无掩中间组合值的相关系数进行攻击。这种方法消除了在学习阶段必须了解掩码的要求，同时避免了高阶DPA对能耗交叉组合的需求，降低了攻击条件，且提高了攻击的效率。实验证实了该攻击算法的可行性和高效性。

侧信道攻击；掩码对策；高阶DPA攻击；神经网络

1 引言

在侧信道攻击中，利用到密码设备中能量消耗变化对其中密钥等私密信息进行攻击的方式，称为能量分析攻击。本质上，这种攻击利用了2类能量消耗的依赖性：数据依赖性和操作依赖性。基于该理论，Kocher等[1]在1999年首次提出DPA攻击的概念与方法，使智能卡芯片等密码设备的安全性遭受了巨大挑战。该攻击基于的原理是，密码设备的能量消耗依赖于算法执行过程中所处理的中间值[2]，如AES加密算法中S盒的输出值。基于这点，通过分析能量消耗的轨迹曲线（简称为“能量迹”），即可得到作为攻击目标的某个中间值，并据此进一步得到加密算法中所使用的密钥等私密信息。因为DPA攻击者不需要了解关于被攻击设备的详细知识信息，所以DPA攻击也迅速成为了比较流行和常用的能量分析攻击方式。

DPA攻击之所以会奏效，是因为密码设备的能量消耗变化依赖于设备所执行加密算法的中间值。因此，防御措施的目标，即是消除这种依赖性，让密码设备的能量消耗独立于密码算法的中间值。目前已公开的抗DPA攻击的各种对策在本质上可以分为2类，即隐藏技术和掩码技术。隐藏技术的基本思想是通过更改生产密码设备硬件的过程，使设备的能量消耗特征发生改变，从而消除能量消耗的数据依赖性；而掩码技术的基本思想则是随机化密码设备所处理的中间值，动机是使设备处理被随机化后的中间值所需的能量消耗与处理实际中间值所需要的能量消耗之间相互独立。该技术的优势在于，相对于隐藏策略来说，掩码策略不需要改变处理器能量消耗特征，在实现可行性和成本方面都具有很大优势。因此，该对策在当前的加密设备中，使用最为广泛。经大量理论及实验证实，使用掩码实现的加密算法，不存在任何的一阶泄露，即无法通过DPA攻击而得到密钥等攻击者想要得到的目标信息。

目前，针对加掩实现的密码算法一般使用到的攻击方式是高阶DPA攻击。在Kocher等[1]首先提出了DPA的概念之后，2000年，针对加掩密码算法，Messerges[3]从各方面完善了阶DPA的定义，并首次提出了二阶DPA概念及其实现方法，以加掩的DES算法为例，通过实验证实了该方法的可行性。基于这些理论，针对掩码策略，更多实用的方案和优化方法被提出。2004年，Jason等[4]提出了他们针对二阶DPA的攻击模型以及相应算法，其中还包括一些攻击技巧，该方案在能量迹较短而相关系数较大时能取得较好的攻击效果。2005年，Marc等[5]提出了一套通用的二阶能量分析攻击的理论基础，并通过估计能量迹峰值的精确数值，进行了二阶DPA攻击算法的研究。高阶攻击的原理是基于能量迹中存在的某种联合泄露来进行的一种能量分析攻击。由于实施DPA攻击时并没有能量迹上信息泄露的准确位置，必须使用遍历任意多个位置的能量消耗组合的方式进行攻击，因而攻击的时间复杂度非常高。在频率域进行能量分析攻击是一种提高DPA攻击效率的有效途径[6]。2014年，Belgarric等提出了一种对能量迹进行时频分析的预处理方法。该方法针对具有一阶防护的软加密实现，通过在能迹上确定二阶DPA攻击所需的2个泄露信息的大致位置范围（窗口），采用傅里叶变换，在频域上进行攻击，从而避免对泄露能耗进行交叉组合的预处理，提高了攻击效率。

模板攻击是一种有学习的能量分析攻击方式，也被用于攻击加掩的密码算法。模板攻击利用对训练设备的已知信息，在学习阶段建立对泄露信息的精确噪声模型，从而极大地提高了攻击的效率。2006年，Oswald等[7-8]首次结合了模板攻击的方式，提出了基于模板的DPA攻击。2007年，Lemke-Rust等[9]提出直接使用模板攻击加掩加密算法的方法。该方法利用训练设备，学习关于泄露中间值和掩码的综合模板，在攻击时同时攻击设备的掩码和密钥。2015年，Lerman等[10]提出使用支持向量机建立关于掩码和去掩后中间值的模板。在攻击中利用掩码的模板首先攻击掩码，去掩后再攻击密钥。同年，Gilmore等[11]提出相同的攻击思路，但其模板采用神经网络。这些研究中提出的方法均需要攻击者在学习阶段了解设备在每次加密中使用的随机掩码。这种要求非常苛刻，并不是在所有攻击中都能具备的。

针对高阶DPA攻击时间复杂度高，而模板攻击学习条件不易满足的问题，本文提出有学习的高阶DPA攻击的方法，在不提高模板攻击中对学习条件的要求的前提下，有效提高高阶DPA的攻击效率。该方法在学习阶段只需要了解训练设备的密钥，利用神经网络建立对无掩中间值的拟合模型。攻击中，利用模型获取带掩中间值，然后利用一阶DPA攻击设备的密钥。由于一阶DPA不需要多个泄露位置上能耗的交叉组合，因此该方法可以显著地提高攻击效率。

2 高阶DPA攻击

DPA攻击具有这样的特性：可以预测出某一个中间值，并可以在攻击中利用这一个预测值。因为这些DPA攻击仅利用一个中间值，故称之为一阶DPA攻击。如果表达假设的过程中使用多个中间值,则称相应的DPA攻击为高阶DPA攻击。

高阶DPA攻击的原理是，多个中间值的某种组合值与多个位置上能耗的某种组合值的相关系数不等于0。而具体的中间值组合方式则需要通过理论分析建模以及多次实验尝试来确定，待定目标则是能量泄露模型及中间值联合泄露位置。

基于上述理论，一种较为简易的二阶DPA攻击的算法示意如图1所示，算法步骤如下。

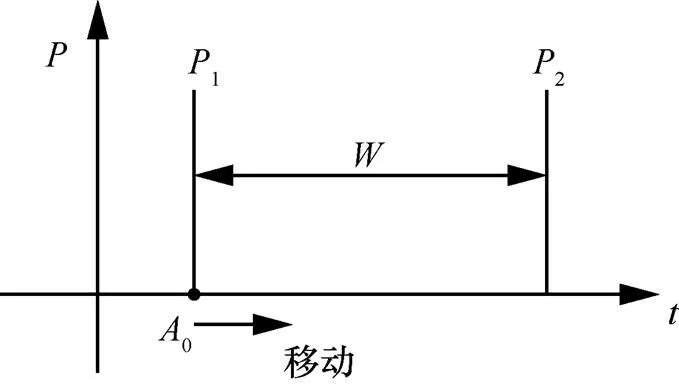
图1 二阶DPA攻击算法示意

该方法基于提出高阶DPA方式的文献，在理论上确实能够适用于掩码实现的加密算法，且在实验中取得了部分效果。但其劣势也很明显，算法在时间复杂度上呈指数形式，攻击成本过大，因为无掩中间组合值与能耗组合值的理论相关系数本身就比较低，这导致了在实践攻击中需要使用更多的攻击能迹。后续我们将结合神经网络算法，重点描述有学习的高阶DPA攻击的实现方式。

3 神经网络

人工神经网络是一种在生物神经网络的启示下建立的数据处理模型，其通过大量的人工神经元相互连接进行计算，并根据外界信息改变自身结构。它的主要工作方式为通过调整神经元之间的权值来对输入的数据进行建模，并最终获得解决实际数学问题的能力。

神经网络最主要的2个特点是自适应性和非线性性。其中，自适应性是指一个系统能够根据外界环境的改变，而对自身结构与作用做出相应的变化的特性；而非线性则是代表具有能够处理显示生活中两者之间非线性关系的能力。在神经网络中，神经元的状态可以表现出数学上的非线性关系，从而可以通过改变神经网络中的权值参数，使神经网络的整体能够完成所需要的非线性映射功能。利用这2个特点，神经网络可以很好地对当前高阶能量分析攻击的方式进行改善，使攻击算法能够具有自适应性，进而保证了攻击的成功率，并且非线性的映射关系能够完美地匹配高阶攻击中的能量泄露模型。

3.1 神经网络类别

根据神经网络的网络结构，可将其分为前向神经网络和递归神经网络。

在前向神经网络中，数据由输入层至输出层单向传播。通常情况下，每层神经元都是全连接到下一层的各个节点，每一个神经元上的激活函数采用sigmoid函数。最简单的一种前向神经网络是“感知器”。感知器神经网络（单层感知器）是一种两层的网络结构，且该结构只能处理线性的数学问题。

其他常用的神经网络类型有线性神经网络、BP神经网络、径向基神经网络、自组织竞争神经网络、反馈神经网络、随机神经网络以及深度神经网络的各种结构等。

本次研究中采用的是前向拟合神经网络，下面专门介绍此类神经网络的结构和训练方法。

3.2 前向神经网络

前向神经网络是对神经元进行分层组织形成的一个具有分层结构的神经网络，其又分为单层前向神经网络和多层前向神经网络。通常情况下，其组织结构中具有多个层，且神经元仅在不同的相邻层之前连接，而不存在同层神经元之间的相互连接。前向神经网络结构示意如图2所示。

图2 前向神经网络结构示意

前向神经网络隐藏层的神经元激活函数一般采用sigmoid函数或tanh函数。

由于神经元的激活函数是非线性的，因此前向拟合神经网络具有非线性拟合能力。在训练中，需要定义一个损失函数，用以计算当前输出与目标值的误差。训练的目标是使该损失最小化。实现的方法是误差反向传播。

各神经元接收前一层的输入，并输出给下一层，传输信号不存在反馈。节点分为2类，即输入节点和计算节点，每一个计算节点可有多个输入，但只有一个输出，通常前向神经网络可分为不同的层，输入与输出节点与外界相连，称为输入层与输出层。其他中间层则称为隐藏层。隐藏层是前向拟合神经网络中位于输入层与输出层之间的中间层，层数为一层或多层。其作用为，把一类输入数据的模式中与其他类输入数据的模式不匹配的属性提取出来，再将提取的属性传递到输出层。最终，将由输出层对数据做出判断。这是一个抽取输入数据属性的过程，本质上实现了输入层与隐藏层之间连接权系数的调整，体现了神经网络结构的自适应性。

在信号传输的同时，采用梯度下降等算法，将误差反向传播到网络中的每个连接上，以此作为更新连接权重的依据。在训练阶段，如果神经网络的输出值与期望值不一致，则将其误差从输出端开始反向传播，在该过程中不断修改各个权值，使输出值向期望值不断靠近，最终完成对神经网络的训练。

4 中间组合值的学习和攻击模型

4.1 基于神经网络的高阶攻击方式

高阶CPA攻击是高阶DPA攻击算法中的一种常用方式。高阶CPA可以攻击采用掩码策略防护后的加密算法，然而由于其攻击中需要计算能量迹上任意多个样本的能耗组合值，其攻击效率很低。为了解决这个问题，本文提出结合神经网络的高阶DPA攻击方法。

高阶DPA攻击方式的效率非常低下。针对这一问题，本文的思路是使用神经网络预测能量迹的中间组合值，进而计算预测中间组合值与猜测中间组合的相关系数。其中的关键在于，在高阶CPA攻击中，将能耗组合值替换为神经网络根据能耗特征向量预测的中间组合值，该神经网络被称为“中间组合值预测网络”，在后文中简称为“预测网络”。预测网络在训练阶段根据训练能耗集，自动习得能耗特征向量与中间组合值的映射关系。理想情况下，神经网络模型能够完全正确地预测中间组合值。虽然在加掩算法中能耗组合值与目标中间组合值之间的相关系数小于1，神经网络将无法完全准确地预测正确的中间组合值，但仍然可以在一定程度上预测正确的中间组合值。这样，预测中间组合值与正确中间组合值之间的相关系数虽然小于1，但仍然大于0。因此，可以将其用于对正确密钥的判断。

这种方法相对于普通高阶CPA攻击的优势如下。

1) 在训练阶段，可以利用神经网络的高度非线性转换能力，自动识别出能耗特征向量中能耗的组合方式，而不需要人为指定能耗组合的计算式。其识别的能耗组合方式有能力排除能量迹特征向量中与目标中间组合值无关的能耗特征，同时对有效的特征提供更好的组合方法。

2) 在攻击时，预测网络直接输入能耗特征向量，例如，指定一段样本区域，就可以得到预测的中间组合值。这样不需要在样本区域中进行全排列以得到能耗组合值，因而极大地提高了攻击效率。

基于神经网络的高阶DPA攻击具体实现步骤分为训练与攻击2个阶段，其中，训练阶段的步骤如下。

1) 针对加掩AES算法能量迹数据及其能量泄露模型，建立相对应的前向拟合神经网络。

3) 利用能量迹数据的能耗特征向量对预测网络进行训练，使之能够将输入的能量迹数据拟合为AES加密过程中的中间组合值。

攻击阶段的步骤如下。

2) 将相关系数降序排列，选择最大相关系数的前个猜测密钥作为候选密钥。

4.2 能迹特征向量的提取与预处理

实验设备采集的能量迹上共包含几十万个样本点，显然，这不可能将所有样本的能耗作为神经网络的输入，并会导致前向拟合神经网络训练的时间复杂度和空间复杂度大为增加。对此，本文需要提取出能迹上包含相关信息泄露的特定样本，从而将能迹转换为能迹特征向量，从而达到保留有效信息、降低数据维度的目的。实现能迹特征向量的提取有2种方案：1) 寻找发生信息泄露的准确位置，称为兴趣点（POI, point of interesting），通过提取兴趣点得到能迹的特征向量；2) 采用能迹上可能发生信息泄露的一段区域，称为兴趣区域（ROI, region of interesting），提取该区域的能耗样本作为能迹的特征向量。

提取兴趣点的方法为采用改进的专用局部搜索算法，对加掩AES密码算法的能量迹数据进行兴趣点查找工作[12]。此方法基于一个由Durvaux等[13]提出的兴趣点检测工具“COSADE 2015 POI”。使用该兴趣点检测算法，就可以明确地找到S盒在输入输出时的信息泄露位置，即兴趣点。该结果将作为第6节中“明确位置的兴趣点输入方式”的实验参数。

采用可视化的方式提取兴趣区域（ROI），根据算法迭代运算在能迹上产生的能耗的规律性变化，确定需要攻击的大致能耗范围。这种方式完全不需要了解训练中使用的掩码，但区域中包含的能耗样本数可能仍然很多，需要采用主成分分析（PCA, principal component analysis）[14-15]进行降维处理。PCA是被各个领域广泛采用的维度缩减方法，其思路是将线性相关的多个特征转换为无关的特征（称为主成分）。主成分包含的信息用方差来表示，方差越大的主成分，包含的原始信息越多。降维时，可以选择方差最大的前个主成分，或选择对方差的贡献率达到某个阈值的前个主成分。

PCA不仅起到维度缩减的功能，其前面几个特征向量包含最多的信息，从而具有最大的信噪比。正因如此，PCA也有提高信噪比的作用。

输入数据归一化处理对前向拟合神经网络非常重要。由于输入的不同位置的能耗存在量级上的差异，PCA处理后得到的主成分也存在量级上的差异，如果直接作为神经网络输入，较大的能量消耗数值在训练中的影响较大，会造成其他能量消耗数据的影响弱化，最终影响神经网络的拟合能力。在本文研究中，由于神经元的激活函数使用到sigmoid函数或tanh函数，其函数值被固定在一个较小的范围之内，因此对数据进行归一化处理是十分必要的。归一化处理技术包括将数据映射为[-1,1]的MapMinMax方法、MVN（mean variant normalization）以及z-score标准化方法等。本文采用z-score标准化对数据进行处理。z-score标准化处理基于数据的均值和标准差，来对数据进行归一化处理。其适用范围是：数据的最大值和最小值均未知，或者是针对超出取值范围的数据。z-score将能耗特征向量的各维映射到均值为0、方差为1的范围。

5 预测网络及其训练

如4.1节所述，预测网络是用于根据能迹特征向量预测加密过程的中间组合值的神经网络。由于能耗数据中包含的噪声很高，信噪比很低，在神经网络的训练中必须采用一些措施才能训练出有效的预测网络。下面，介绍预测网络的模型及其训练方法。

5.1 预测网络模型

由于本文需要使用神经网络来预测中间组合值的具体数值，因此采用拟合神经网络，即神经网络的输出只有一个神经元。一个具有输入层、隐藏层、输出层的前向神经网络结构示意如图3所示。网络各层的神经元采用全连接。其中，输入层的神经元数量等于能迹特征向量的维度，输入层神经元为线性激活函数；隐藏层可以包含多层，其层数和各层的神经元数量与训练数据集的大小、特征的数量相关，需要在实验中确定，隐藏层神经元的激活函数可以采用sigmoid、tanh、ReLU等；输出层仅包含一个神经元，其激活函数为线性函数，输出网络的拟合值。

图3 前向拟合神经网络结构示意

预测网络的输入为能迹特征向量，输出为拟合的中间组合值。在训练阶段，训练的目标是尽可能减小预测网络的拟合中间组合值与真实中间组合值的差异。因此训练的损失函数采用最小均方差（MSE）。

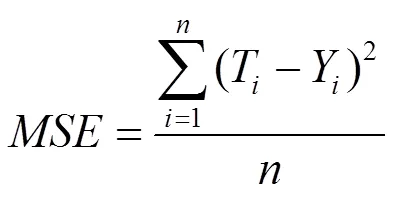
训练中采用误差梯度反向传播更新网络的连接权重。具体的算法可以采用LM（levenberg marquardt）算法或量化共轭梯度（SCG, scaled conjugate gradient）法等。

5.2 训练中防止过拟合

过拟合是指训练得到的映射模型过分与训练数据匹配，导致模型失去了泛化能力。过拟合示意如图4所示。在训练集中，输出与目标拟合程度很高，而对于非训练数据，拟合程度则很差。过拟合现象的表现形式为，当训练过程进行到一定程度时，模型对训练数据和验证数据的损失分布减小到一定程度。此时，如果继续对神经网络进行训练，训练集的损失会进一步减小，而验证集的损失反而开始逐渐增大。

图4 过拟合示意

一般情况下，过拟合由于过度训练，造成模型中体现出过多的、仅出现在训练集中的“特征”。为了避免出现过拟合，神经网络训练时，一般将训练数据划分为2个子集：训练集和攻击测试集。当训练集的性能处于连续上升的状态，而测试集的性能却在同时出现连续下降的状态，就表明出现了过拟合。此时，应该停止对神经网络的训练。这种防止过拟合的方法称为“early ending”。

然而，造成过拟合还有另一个因素，即训练数据中包含了过多的噪声。对于能迹特征向量，其信噪比很低，过拟合在训练的极早期可能出现。此时，验证集的损失仍然非常大，网络的拟合能力非常差。此时，必须采用正则化训练方法来防止此类过拟合。

首先，正则化就是在最小化经验误差函数之上添加约束，该约束可以解释为先验知识，即正则化参数等价于对参数引入先验分布。约束具有引导的作用，在优化误差函数时倾向于选择满足约束的梯度减少的方向，使目标函数的最终解倾向于符合先验知识。

其次，正则化解决了逆问题的不适定性，产生的解是存在且唯一的，同时，也依赖于数据。噪声对于训练的影响就会变弱，训练中就不会出现过拟合现象，而且，如果正则化适当，则训练中数学模型的参数也就更加符合真实情况。

L2正则化项有着使神经网络中权重方差变小的效果。较小的权重方差代表神经网络的复杂程度低，对训练集数据的拟合程度是恰当的，不会存在对训练集数据过多无关细节的拟合。在实际应用中，使用到L2正则化后神经网络的训练效果，通常优于未经L2正则化处理过的神经网络训练效果，即过拟合很大程度上被抑制了。

6 实验分析

为验证4.1节提出的基于神经网络的高阶攻击方法，本文对AES加掩加密设备进行了攻击实验。实验分为2个部分，分别采用发现兴趣点的方法和设置兴趣区域的方法获取能迹特征向量，对神经网络进行训练和攻击，以对比这2种方法的优劣。

6.1 实验目标设备及数据采集

本次实验基于一个执行在智能卡上的AES算法。实验设备由示波器、智能卡及其读卡器、计算机、电源等组成，如图5所示。计算机负责向读卡器下发命令控制智能卡运行AES加密算法，同时，通过USB线向智能卡下发明文信息。并且，在智能卡工作时，给示波器触发信号，用以进行能量迹采集。示波器将采集到的能量迹信息通过双绞线发送到计算机中进行存储。其中，示波器的采样信号为读卡器供电处串联电阻的两端电压。在能量迹数据测量与采样结束之后，再通过相应的分析软件对信号进行进一步的处理。

图5 实验平台结构示意

计算机控制智能卡实现随机明文的加密运算，并通过示波器采集每次加密运算中第一轮运算所产生的能量迹，采样率设为250 MHz。对采集的第一轮运算的功耗进行简单滤波处理，如图6所示。

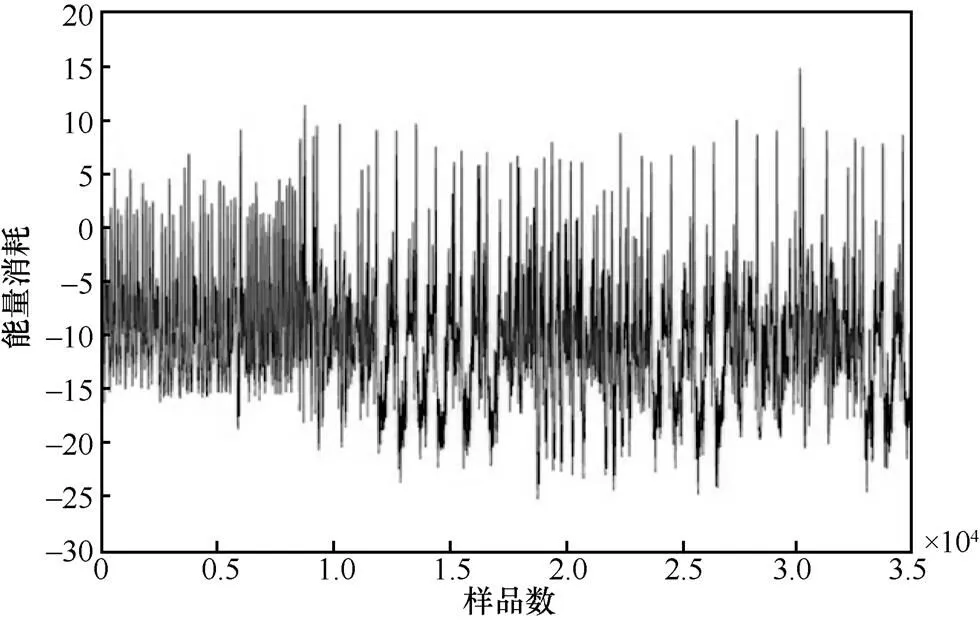
图6 加掩AES算法的能量轨迹示意

本文的攻击对象为S盒的输入输出，对于攻击者来说，有效的信息为关于S盒输入中间数据操作和S盒输出中间数据操作所产生的功耗，为减少无效的功耗信息，提高信噪比，后续可对能量迹数据进行归一化处理。

采样完毕后，我们得到了关于加掩实施AES算法的能量迹10 000条，并将其作为样本进行后续的攻击实验。样本分为训练集和攻击测试集两个部分，其中，8 000条能量迹作为训练集，2 000条能量迹作为攻击测试集。

6.2 能迹特征向量提取与预处理

1) 通过发现兴趣点提取能迹特征向量

根据4.2节中寻找兴趣点的方法，在加掩AES算法的能量迹中第一轮S盒的范围内找到输入与输出部分的2个明确的兴趣点位置。在包含2 000条能量迹的攻击测试集中，该位置将生成2 000×2的能迹特征向量矩阵。

2) 通过指定兴趣区域提取能迹特征向量

通过4.2节中介绍的平均能迹的可视化方法，可以发现轮操作范围及S盒的操作范围。

加掩AES算法第一轮加密的能量消耗轨迹如图7所示。从图7可以明显看出第一轮中的16个S盒操作的能量消耗变化规律。虚线框的范围就是第一个S盒置换操作的样本范围。

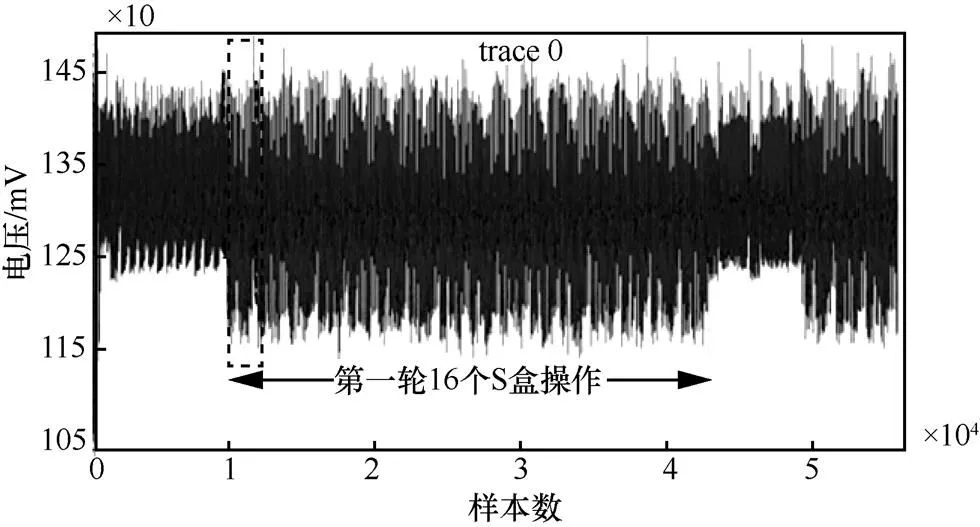
图7 加掩AES算法第一轮加密的能量消耗轨迹

可以看出，一个S盒范围内的样本数较多，其中，兴趣区间中的样本数量达到了4 000左右，即实验中使用到的能量迹数据仍然过于庞大。因此本文中将使用到更加适合基于神经网络的高阶攻击方式的PCA降维技术，对能量迹进行处理。

使用4.2节中描述的PCA步骤，根据可视化的方法选择兴趣区间，对兴趣区间上的数据进行处理，首先进行特征值分解，然后将能量迹转换为特征向量。将贡献度设置为0.8，并将能量迹数据的主成分对应的特征向量作为降维结果，在包含2 000条能量迹的攻击测试集中，可以将2 000×4 000的矩阵缩减为2 000×22的能迹特征向量矩阵。

3) 能迹特征向量的预处理

在得到能迹特征向量之后，使用训练特征向量集中的数据得到z-score的参数，即总体样本数据的数学期望以及标准差，并使用该参数同时对训练特征向量集和验证特征向量集进行归一化处理。

6.3 神经网络结构与训练

实验中采用在5.1节中描述的3层前向拟合神经网络。第一层为数据输入层；第二层为隐藏层，起到非线性转换的作用，其中的神经元具有非线性响应特征，对第一层的输入进行非线性转换，响应函数采用默认的tanh函数；第三层为输出层，仅包含一个神经元，对第二层的输出进行线性转换。其中，输入层的大小（包含的神经元数量）取决于输入数据的维度；隐藏层的大小，一般难以确定最优值。在一般情况下，更大的输入维度和更强的非线性转换，需要更大的隐藏层。但在“需要”的隐藏层大小上再增加其神经元数量，对非线性转换并没有提高作用，却会增加计算量。在实践中，隐藏层的大小通常由多次实验的结果来确定。

在本次实验中，神经网络的输入是能耗特征向量，输出是加密过程的中间值组合值。需要说明的是，对每个需要攻击的子密钥，需要建立相应的神经网络，用于训练针对该子密钥的模板。前向拟合神经网络作为模板时的实验结构如图8所示。

图8 前向拟合神经网络实验结构

具体的训练步骤如下。

接下来，本文以明确兴趣点的攻击方式训练参数为例，介绍fitnet拟合神经网络训练结束条件采用的默认结束条件，训练结束时的各指标状态如图9所示。在训练进行的过程中，该图中数据的变化代表着训练进度。

图9 训练结束时的各指标状态

1) Epoch为训练次数，在其右边显示的是最大的训练次数，本实验中设为1 000，而进度条中显示的是实际训练的次数，从图9可以看出，本次训练进行了8次后结束。

2) Time为训练时长，也就是本次训练进行的时间。

3) Performance为性能指标，在本次训练中为最小均方差MSE。进度条中显示的是当前的，右侧显示的则是设定的阈值（若训练过程中值小于阈值，则结束训练）。

4) Gradiengt为梯度，进度条中显示的是当前的梯度值，右侧显示的则是设定的梯度值阈值（若训练过程中梯度值小于阈值，则结束训练）。

6) Validation Check为泛化能力检查，若连续6次训练中误差未能降低，则结束训练。

上述6个参数中有5个参数代表着训练的结束条件，并且该5个结束训练的条件只需达成一个条件即可结束训练。从图9可以看出，本次训练是因为泛化能力检测而结束，即第二次训练时达到最小值，且在之后的6次训练中未能降低，因此在第8次训练之后结束训练。

本实验对比了2种能量迹特征向量的生成方式，分别是提取兴趣点和使用能量迹中一段兴趣区间。对比实验的目的是为了证实该攻击方式可以在事先不能找到明确的泄露位置时，对加掩实现的AES算法进行成功的攻击。另外，通过比较训练效果及攻击性能等参数，可以证实神经网络能够自动地找到能量迹中更加合适的中间值组合方式。在提取兴趣点作为能量迹特征向量时，神经网络输入层共含有2个节点；在使用兴趣区间作为能量迹特征向量时，神经网络输入层共含有多个节点，在本实验中输入层大小为22。

在拟合神经网络的训练中，使用到的训练集数据被分为train set、validation set和test set这3个部分。其中，train set是用来训练模型或确定模型参数的，如神经网络中的权值等；validation set是用来做模型选择的，即模型的最终优化与确定，如神经网络的结构；test set是用来检验最终选择最优模型性能的，目的是为了测试已经训练好的模型的推广能力。本实验将训练集的70%作为train set、15%作为validation set、15%作为test set，以此方式进行神经网络的训练。

2种方式的训练结果分别如图10和图11所示。其中，在明确兴趣点输入神经网络的训练方式中，最小均方差值为2.061 0；而以兴趣区间上的多点输入神经网络的训练方式中，最小均方差值仅为1.982 8。可以看出，后者的训练效果要优于前者，即后者训练出的神经网络的拟合结果将更为精确。

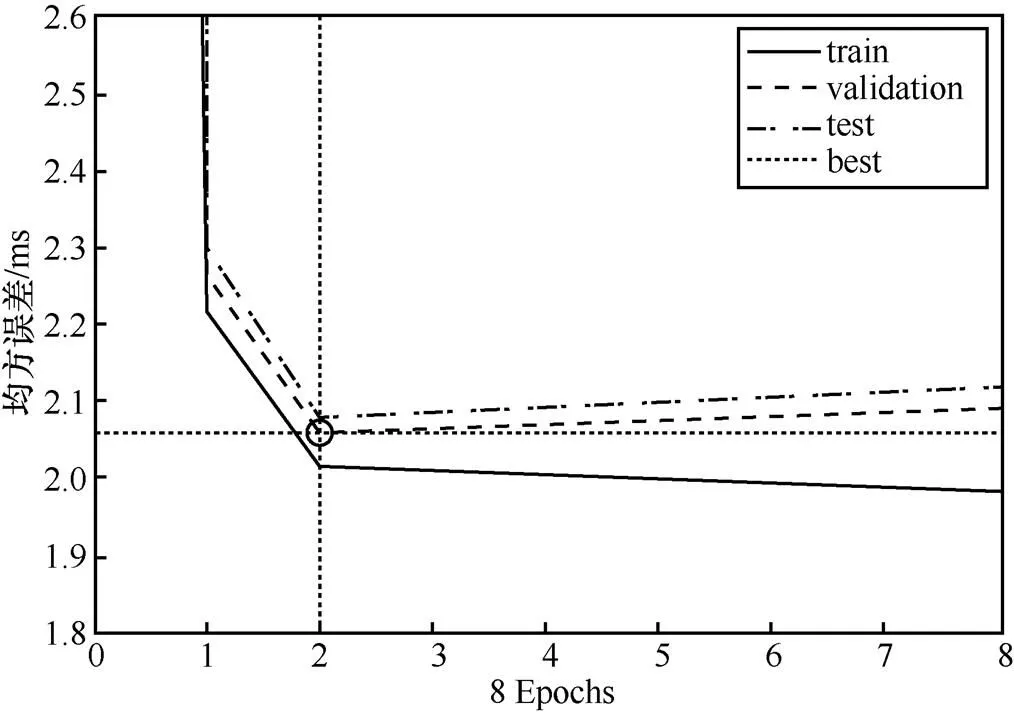
图10 以明确兴趣点输入神经网络的训练结果

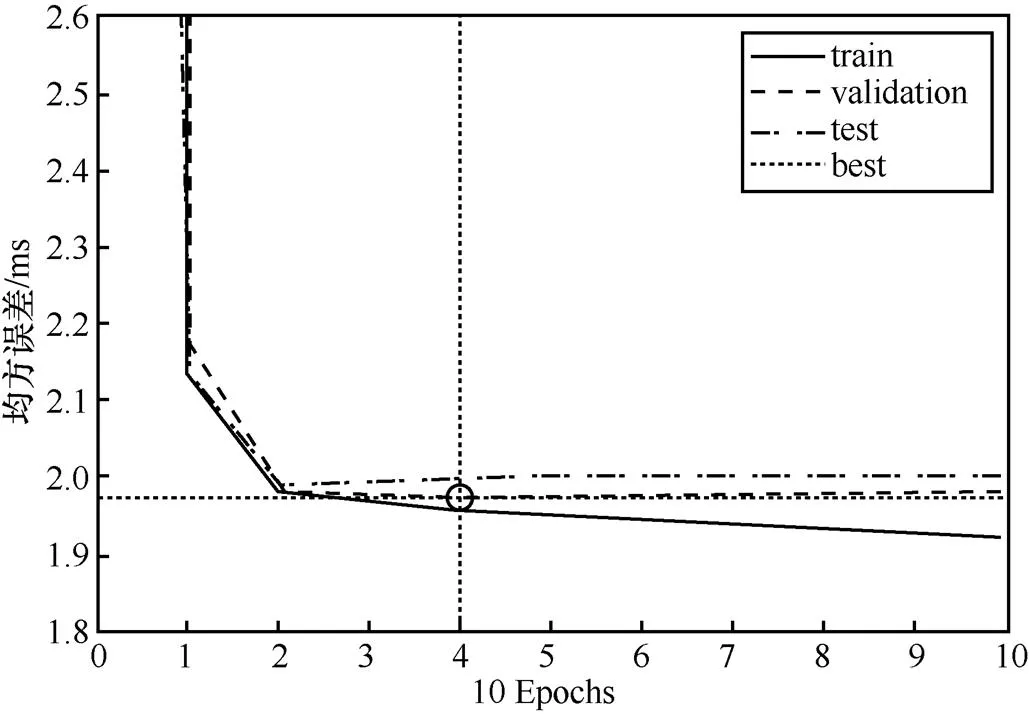
图11 以兴趣区间上多点输入神经网络的训练结果

然后，针对以兴趣区间上的多点输入神经网络的训练方式，我们将隐藏层激活函数由默认的tanh函数改为sigmoid函数做对比实验，其训练结果如图12所示。最小均方差值为1.977 5，其训练结果与隐藏层使用tanh函数作为激活函数的训练结果相差不大。

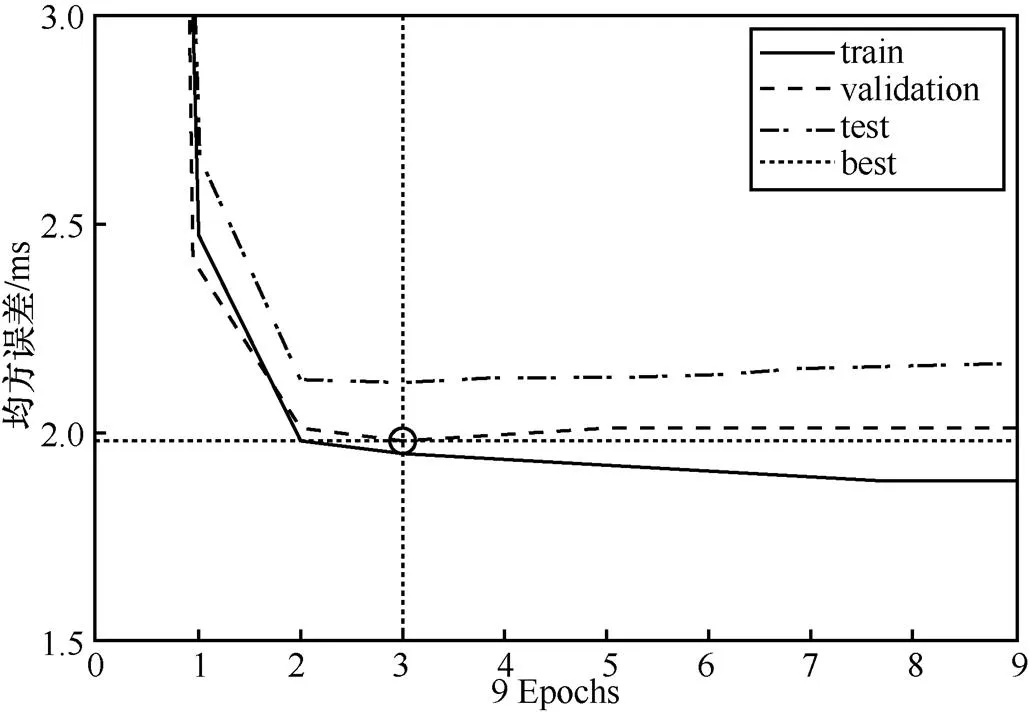
图12 隐藏层使用sigmoid作为激活函数的训练结果

最后，我们将通过修改隐藏层的层数，进行神经网络训练进一步的对比实验。为确保神经网络参数数量基本不变，我们将隐藏层的层数改为2层，其中，每一个隐藏层分别含有40个神经元。该神经网络的训练结果如图13所示。

本次训练中，最小均方差值为2.003 2，其训练结果与相较于单层隐藏层的神经网络而言有所下降。原因是神经网络的层数越多，针对非线性关系的拟合能力就会越强。同时，发生过拟合现象的可能性也将增大。从图13可以看出，在训练的后半部分，随着train set误差的逐步减小，validation set和test set的误差有着明显的升高现象，这是在之前对比实验中未出现的，说明该神经网络的拟合能力过强，从而导致了过拟合现象的发生。由此可以看出，隐藏层的层数及节点数量均需要基于理论分析和大量实验才能够确定。

图13 具有2个隐藏层的神经网络训练结果

6.4 基于神经网络的高阶CPA攻击

在攻击阶段，前向拟合神经网络根据一个输入能耗向量（与训练能耗向量进行同样的归一化处理），输出一个中间组合值的拟合值。获取该特征向量的方式分为2种，即以明确兴趣点作为特征向量与将一段兴趣区间上的多点作为特征向量。

在采用多条能迹进行攻击时，需要计算对某个猜测的子密钥，这些攻击能迹的联合概率。本实验采用隐藏层大小为100的前向拟合神经网络作为模板，输出为汉明重量的拟合值。输入分别使用明确的兴趣点（采用第一轮中第一个S盒的输入和输出的2个准确的泄露位置的能耗）和兴趣区间上的多点这2种方式进行攻击性能对比。

接下来，使用之前训练好的前向拟合神经网络对攻击测试集中的能量迹对加掩的AES算法的加密能迹进行高阶攻击，攻击目标为加掩AES算法第一轮加密中S盒的轮密钥。得到神经网络输出后计算目标相关系数并排序，将正确的轮密钥与排序结果进行对比。

具体的攻击步骤如下。

基于神经网络的高阶DPA攻击算法流程如图14所示。

图14 基于神经网络的高阶DPA攻击算法流程

在攻击测试集包含2 000条能量迹的攻击中，以明确兴趣点作为输入的方式，神经网络输入层大小为2，正确的轮密钥排在结果中的第一位，相关系数为0.089 1，排在第二位的猜测轮密钥的相关系数为0.070 8。而以兴趣区间上的多点作为输入的方式，神经网络输入层大小为22，正确的轮密钥排在结果中的第一位，相关系数为0.177 1，排在第二位的猜测轮密钥的相关系数为0.075 0。

由于第二种攻击方式得出正确结果的相关系数与错误结果相差更大，而第一种攻击方式的结果中各个猜测密钥之间的相关系数相差很小，这证明了使用兴趣区间上的多点作为神经网络输入的方式，攻击性能要明显优于使用明确兴趣点作为神经网络输入的方式，不同能耗特征向量生成方式的实验对比如图15所示。从图15中2种输入方式的结果比较可以看出，输入为兴趣区间上多点的方式，得到正确密钥对应的相关系数，与错误猜测的密钥相比，（横轴为1的函数值与其他位置的函数值相比）差距更加明显，使攻击的成功率得到了很大的提高。

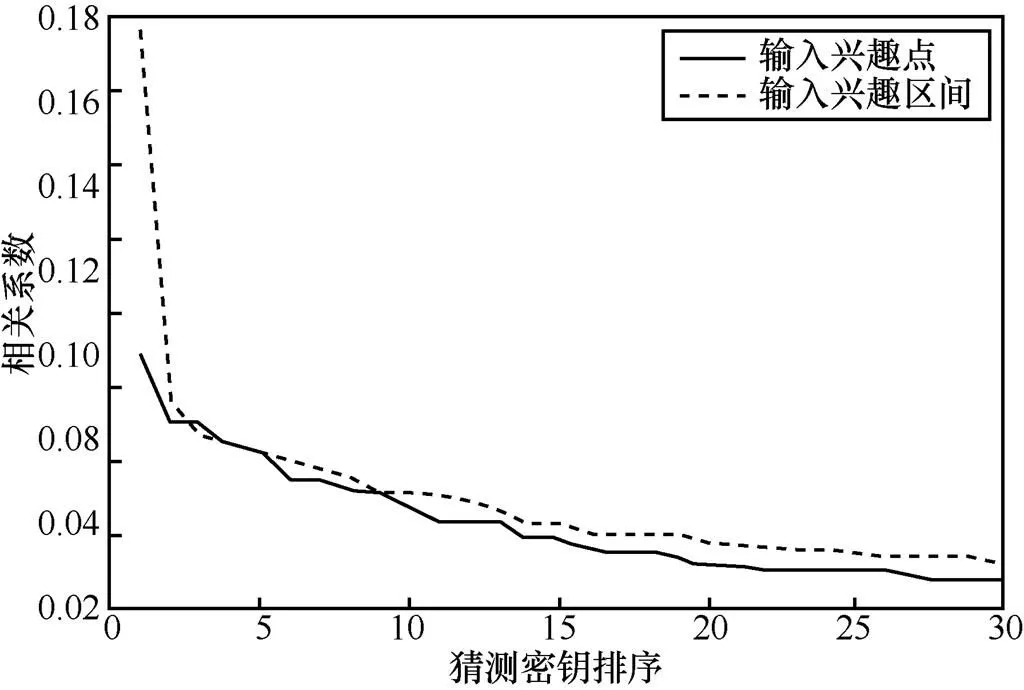
图15 不同能耗特征向量生成方式的实验对比

以上结果证明，虽然2种输入方式都可以攻击成功，但以兴趣区间上的多点作为输入的方式，攻击性能要明显优于以明确兴趣点作为输入的方式。这是因为，仅通过2个兴趣点来提取信息会导致大量泄露信息的丢失，而使用到兴趣区域的提取方式则能够更好地保留这些泄露信息，并通过神经网络来有效组织它们的组合方式，最大程度地利用了能迹上的泄露信息。

为了验证本文提出的基于神经网络的高阶DPA攻击的攻击能力，我们又进行了最少攻击能迹的实验。实验中，我们将不断减少攻击中采用的攻击能迹数，以正确密钥出现在攻击的候选密钥第一位时所需的最少能迹数量来衡量攻击的能力。最终，可以确定该方案至少需要使用500条能量迹方可对加掩的AES算法攻击成功。相较于二阶DPA攻击方案中攻击成功所需的1 000条能量迹而言，该方案在攻击条件上已有大幅度提高。这是因为神经网络强大的非线性拟合能力及自适应性使该攻击方式能够在与高阶DPA攻击相同的条件下，找到能耗组合值与中间值组合值更大的相关系数，从而提高了攻击效率。

7 结束语

神经网络在高阶DPA攻击中体现出较为明显的优势，这是因为神经网络具有较强的非线性映射能力，能够自动发现输入能耗数据与目标值（接近）最佳的非线性映射方式。

在能量分析攻击中，我们主要研究了前向拟合神经网络在高阶DPA攻击中的应用，并在攻击质量上取得了明显的提高。实验表明，神经网络具有强大的特征识别能力和非线性转换能力，能够提供比其他机器学习算法更好的学习效率及拟合结果，有利于减少训练和攻击能量迹的数量。在高阶攻击中，特别在我们设定的训练数据未知掩码的情况下，对于能耗与中间组合值的相关性，目前运用的神经网络方法已可有效地进行学习及拟合过程。

在今后的研究中，我们将致力于探索深度神经网络提取更多特征，以便于提高与中间组合值相关性的方法。

[1] KOCHER P, JAFFE J, JUN B. Differential power analysis[C]//Annual International Cryptology Conference. 1999: 388-397.

[2] POPP T, MANGARD S, OSWALD E. Power analysis attacks and countermeasures[J]. IEEE Design & test of Computers, 2007, 24(6): 535-543.

[3] MESSERGES T. Using second-order power analysis to attack DPA resistant software[C]//International Workshop on Cryptographic Hardware and Embedded Systems. 2000: 238-251.

[4] WADDLE J, WAGNER D. Towards efficient second-order power analysis[C]//International Workshop on Cryptographic Hardware and Embedded Systems. 2004: 1-15.

[5] JOYE M, PAILLIER P, SCHOENMAKERS B. On second-order differential power analysis[C]//International Workshop on Cryptographic Hardware and Embedded Systems. 2005: 293-308.

[6] 王敏, 吴震, 饶金涛, 等. 针对密码芯片频域互信息能量分析攻击[J]. 通信学报, 2015, 36(Z1): 131-135.

WANG M, WU Z, RAO J T, et al. Mutual information power analysis attack in the frequency domain of the crypto chip[J]. Journal on Communications, 2015, 36(Z1): 131-135.

[7] OSWALD E, MANGARD S, HERBST C, et al. Practical second-order DPA attacks for masked smart card implementations of block ciphers[C]// Cryptographers’ Track at the RSA Conference. 2006: 192-207.

[8] OSWALD E, MANGARD S. Template attacks on masking— resistance is futile[C]//Cryptographers’ Track at the RSA Conference. 2007: 243-256.

[9] LEMKE-RUST K, PAAR C. Gaussian mixture models for higher-order side channel analysis[C]//International Workshop on Cryptographic Hardware and Embedded Systems. 2007: 14-27.

[10] LERMAN L, BONTEMPI G, MARKOWITCH O. A machine learning approach against a masked AES[J]. Journal of Cryptographic Engineering, 2015, 5(2): 123-139.

[11] GILMORE R, HANLEY N, O'NEILL M. Neural network based attack on a masked implementation of AES[C]//2015 IEEE International Symposium on Hardware Oriented Security and Trust (HOST). 2015: 106-111.

[12] DURVAUX F, STANDAERT F X. From improved leakage detection to the detection of points of interests in leakage traces[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. 2016: 240-262.

[13] DURVAUX F, STANDAERT F X, VEYRAT-CHARVILLON N, et al. Efficient selection of time samples for higher-order DPA with projection pursuits[C]//International Workshop on Constructive Side- Channel Analysis and Secure Design. 2015: 34-50.

[14] 张洪欣, 李静, 张帆, 等. 基于能耗旁路泄露的密码芯片模板攻击算法研究[J]. 电波科学学报, 2015, 30(5): 987-992.

ZHANG H X, LI J, ZHANG F, et al. A study on template attack of chip base on side channel power leakage[J]. Chinese Journal of Radio Science, 2015, 30(5): 987-992.

[15] 阮越, 陈汉武, 刘志昊, 等. 量子主成分分析算法[J]. 计算机学报, 2014, 37(3): 666-676.

WAN Y, CHEN H W, LIU Z H, et al. Quantum principal component analysis algorithm[J]. Chinese Journal of Computers, 2014, 37(3): 666-676.

High order DPA with profiling

WU Zhen1, WANG Yi1, ZHOU Guanhao1,2

1. Institute of Cyberspace Security, Chengdu University of Information Technology, Chengdu 610225, China 2. Beijing Intelligent Cloud measuring equipment Technology Co., Ltd., Beijing, 102300, China

In side channel attack, the masking implementation is one of the most popular counter measures again first order DPA. Presently, high order DPA and high order template attack are often used to attack against masking counter measures. High order DPA, however, targets joint leakage of multiple types of information and therefore needs cross combination of powers at corresponding positions, which is the root of the inefficiency of high order DPA. High order template attack, on the other hand, has to know the random mask in each encrypting at its learning phase, which is rarely satisfied for most adversaries. Be aware of these shortcomings and limitations, the algorithm of high order DPA with profiling used neural network to establish the model of fitting the combination of un-masked intermediate values. Attacking was based on the correlation coefficient between the fitted combination intermediate value and the guessing combination intermediate value. This method eliminated the requirement of knowing the masks at the learning phase of template attack and the requirement of cross combination of powers for high order DPA, and therefore lowered the requirement of learning as well as improved attacking efficiency. Experiments have confirmed the feasibility of this algorithm, as well as its efficiency.

side channel attack, mask countermeasure, higher order DPA attack, neural network

TP309.1

A

10.11959/j.issn.1000−436x.2018164

吴震（1975−），男，江苏苏州人，成都信息工程大学副教授，主要研究方向为信息安全、密码学、侧信道攻击与防御、信息安全设备设计与检测。

王燚（1968-），男，四川成都人，博士，成都信息工程大学教授，主要研究方向为机器学习、侧信道攻击与防御、自然语言处理。

周冠豪（1993-），男，江西南昌人，北京智慧云测设备技术有限公司技术工程师，主要研究方向为信息安全、机械学习、侧信道攻击与防御、物联网安全。

2018−04−03；

2018−07−28

王燚，wangyi1177@cuit.edu.cn

国家重大科技专项基金资助项目（No.2014ZX01032401-001）；四川省科技计划基金资助项目（No.2017GZ0313）；四川省教育厅科研基金资助项目（No.17ZB0082）

The National Science and Technology Major Project of China (No.2014ZX01032401-001), Sichuan Science and Technology Programmer (No.2017GZ0313), Sichuan Provincial Education Department Scientific Research Project (No.17ZB0082)