基于EAHP的地面无人作战平台性能评价方法
2018-10-18孟凡凯马海宁俞锦涛孙少辉
孟凡凯,马海宁,俞锦涛,孙少辉
(陆军炮兵防空兵学院,安徽 合肥 230031)
无人作战平台是指无人驾驶的、完全按遥控操作或预编程序自主运作的、携带进攻性或防御性武器遂行作战任务的一类平台[1]。地面无人作战平台是无人作战平台的一种,主要包括军用无人战斗车辆、通用后勤服务无人车辆和小型单兵机器人等[2]。地面无人作战平台能够代替士兵独立遂行侦察、攻击等各种军事任务,可减少人员伤亡和提高战斗效率。地面无人作战平台非常灵活,可以穿越复杂地形,可以装备多种类任务载荷,能极大提高部队的战斗力[3]。鉴于以上优点,近年来,地面无人作战平台得到各国军方的关注。但在平台实际研发过程中,不同研发机构对地面无人作战平台的评价体系不一致,致使其作战性能得不到公正评价。显然,制定一套统一的评价体系对地面无人作战平台的性能进行评价是十分必要的。本文主要从地面无人作战平台的自身机动能力和智能感应能力两个方面对其综合性能进行评价。
1 指标评价体系的建立
通常讲,地面无人作战平台应具有三种能力:自身机动能力、智能感应能力和完成任务能力,我们从这三个能力出发构建指标评价体系。但是,地面无人作战平台完成不同作战任务需要配置相应任务载荷,因此,不同任务类型的地面无人作战平台完成任务能力不具备可比性。所以,本文只针对地面无人作战平台的自身机动能力和智能感应能力进行评价。
1.1 自身机动能力
自身机动能力是指作战平台从一个位置移动到另一个位置的能力,可由快速机动能力、灵活机动能力、越障能力三个子能力进行评价。
1) 快速机动能力:可由作战平台的最高速度和平均速度来评价;
2) 越障能力:可由爬坡能力、松软地面通行能力、涉水能力、跨壕能力和最长行驶距离来评价;
3) 灵活机动能力:可由加速能力、制动能力、转向能力来评价。
1.2 智能感应能力
各国对智能感应能力的定义不一,美国“无人系统自主级别(ALFUS)工作小组”将其定义为:为了实现操控人员通过人机接口所赋予的目标,无人系统自身所具有的感知、分析、通信、规划、决策和执行等综合能力[4]。国内学者将其定义为:在复杂多变的未知环境中主动地执行预定任务,通过环境感知、决策规划,有计划、有目的地产生智能行为以适应环境、改变现状,从而达到预定的目标[5]。通过以上表述,我们可知地面无人作战平台智能感应能力的本质是感知外界环境变化、获得输入信号、做出智能决策、生成执行指令,进而对环境变化做出反应。综上可知,平台的智能感应能力可从环境感知能力和环境反应能力两个方面进行评价。
1) 环境感知能力:是指地面无人作战平台通过传感器感知外界环境变化,并通过数学模型将其转化为作战平台可接受的数字信号,可由感知范围、建模精度、模型更新频率来对环境感知能力进行评价。
2) 环境反应能力:是指地面无人作战平台通过输入的数字信号进行正确判断,做出智能决策,生成执行指令,并执行指令的能力。主要表现在两个方面:一是地面无人作战平台被赋予使命任务后,根据外部环境和内部信息准确有效地进行任务分解形成元任务集,并根据当前元任务快速地做出正确的行为决策;二是表现在自主导航能力方面,地面无人作战平台能够根据环境的变化、自身所处位置的变化和任务的变化,实时进行局部路径的合理规划,并发出机动指令来跟踪这些路径。因此,环境反应能力可由任务规划与决策能力、平台定位精度、路径规划正确率、指令执行速度、指令执行精度对环境反应能力进行评价。
综上所述,可建立如图1所示的指标评价体系。
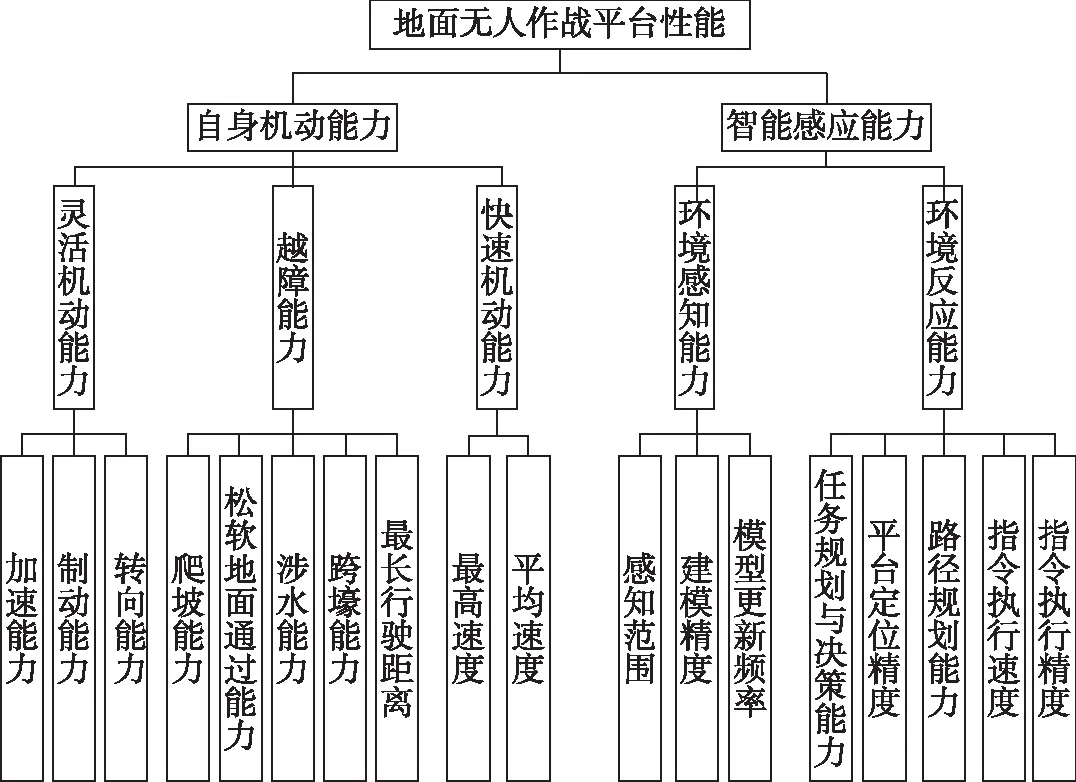
图1 地面无人作战平台指标评价体系
2 评价指标的打分及归一化处理
得到指标评价体系之后,我们可对各评价指标进行打分,然后根据各个指标的权重,对平台的性能进行综合评价,下面介绍各评价指标的打分及归一化处理方法。
2.1 自身机动能力
2.1.1 灵活机动能力
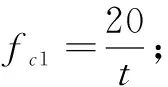


2.1.2 越障能力

2) 松散地面通过能力:平台通过地面时,平均接地压强。接地压强越小,通过松散地面的能力越强。按照定性评估,分为5个等级,差,较差,中、较好、好,归一化后的评价值分别为0、0.3、0.5、0.7、1。
3) 涉水能力:平台所能通过的涉水深度占规定宽度水面的最大深度为h,通常以1 m为界,高于该标准的归一化值都为1,其他为fc6=h;
4) 跨壕能力:平台所能通过的涉水深度占规定宽度水面的最大深度为w,通常以1 m为界,高于该标准的归一化值都为1,其他为fc7=w;

2.2 环境感应能力
2.2.1 环境感知能力

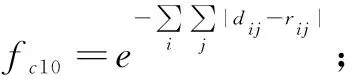
3) 模型更新频率:在规定的战场环境下,模型的更新次数以单位时间更新8次为适中值,归一化后的更新评价值:
2.2.2 环境反应能力
1) 任务规划与决策能力:用地面无人作战平台正确规划与决策的次数占总规划与决策次数的比例fc12来衡量;
2) 平台定位精度:在规定的战场环境下,用地面无人作战平台定位的坐标与实际坐标误差的归一化均方差来衡量,记为fc13;
3) 路径规划能力:用地面无人作战平台在运行过程中成功规划路径的百分比来衡量,记为fc14;

5) 指令响应精度:可用路径规划精度来衡量,即规划路径与既定路径(长度一定)之间的面积S,归一化后用fc16=e-S表示。
3 权重计算
获得各评价指标的分值之后,通过专家打分的方式确定各指标的权重,在确定权重时,通常采用层次分析法(AHP,Analytic Hierarchy Process)。但是AHP存在一定缺陷,即模糊判断矩阵明确化和需要一致性检验。我们使用可拓展的层次分析法(EAHP,Earp Analytic Hierarchy Process),用区间数代替点值数构造可拓展判断矩阵,克服了模糊判断矩阵明确化的问题。
3.1 构建可拓判断矩阵
在同一准则层下,专家按照SAATY 提出的互反性 1-9 标度法对各个指标的重要性进行两两比较,依次,可以建立可拓判断矩阵:

3.2 计算判断矩阵的权重
下面计算矩阵A=
1) 求A-,A+最大特征值所对应的具有正分量的归一化特征向量x-,x+;
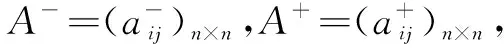
(1)
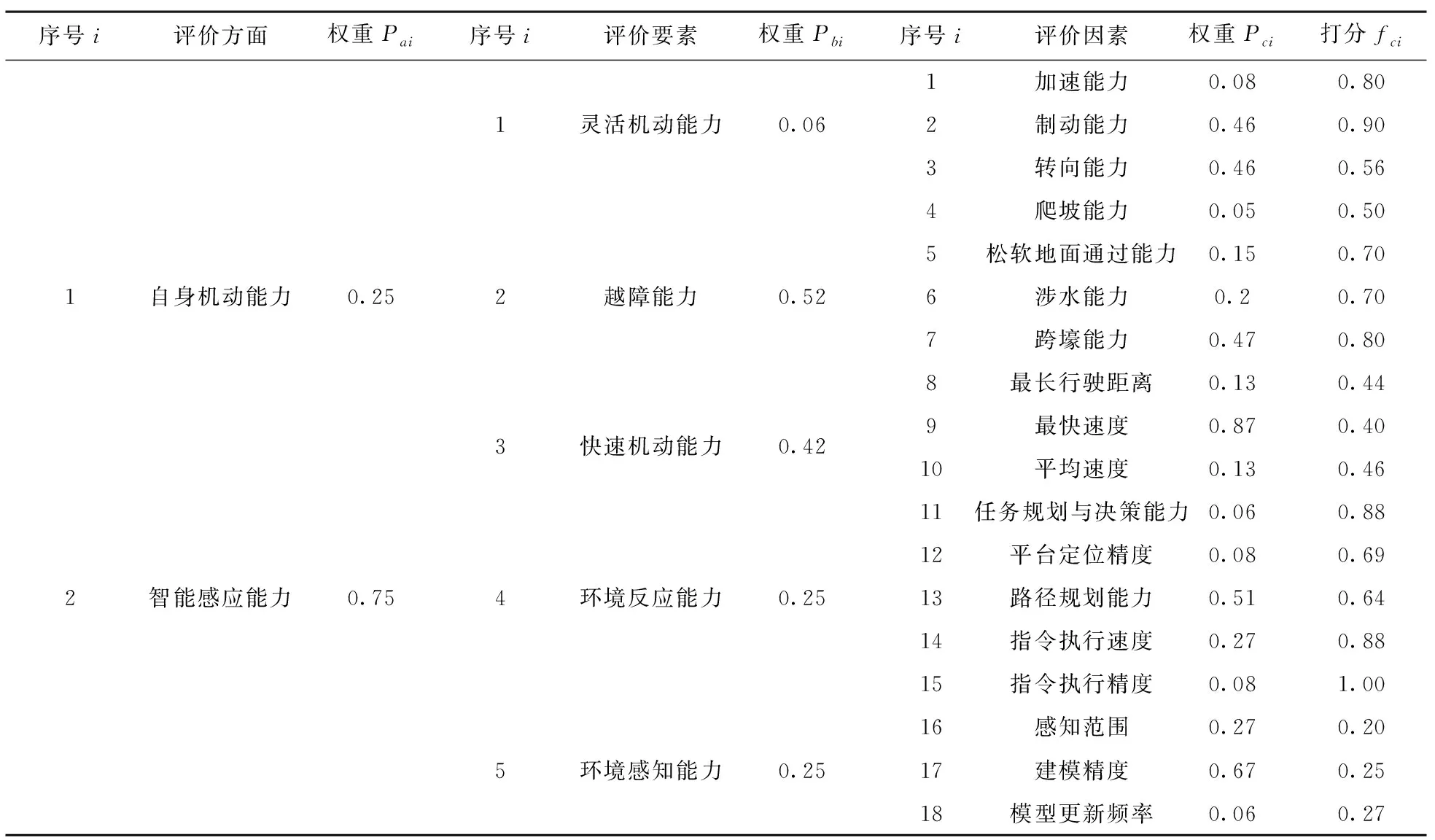
其中k,m为全体正实数,且k,m满足0 3) 一致性判断。当0 4) 计算权重 S=(S1,S2,S3…Snk)T= (2) 其中,Snk表示第k层,第n个元素对上一层的某个因素的可拓区间权重。 (3) 其中i,j=1,2,…,n,i≠j; Pi为第i个元素对其上一准则层的某因素的权重; P=(P1,P2,P3,…Pn)T表示某一准则层上n个因素分别对上一准则层的某因素的权重向量; 当h=1,2…,nk-1时,可得矩阵: (4) (5) Wk=PkPk-1…P3W2,W2即是单项排序向量[6]。 假设某科研机构,研发一台地面无人作战平台,经测试,其各项评价指标的性能经过归一化处理之后如表1所示。 表1 评价指标分数表 现按照所建立的模型对该平台的性能进行评价。 根据指标评价体系中的各个评价指标,按照1-9标度法构建可拓区间数判断矩阵,如表2所示。 我们由上至下对评价体系中每个准则层进行比较,得到可拓区间判断矩阵,然后计算出各指标权重系数。详细数据见表3。 表2 权重打分表 由表2可知: 计算可得 m=1.0545,X-=(0.1815,0.4712,0.3473)T 按照同样的方法可得 k=0.9414,X+=(0.1768,0.4773,0.346)T 其中,0≤k≤1≤m,所以可拓区间判断矩阵的一致性较好。 由式(3)得 S1=<0.1709,0.1864>,S2=<0.4436,0.5033>,S3=<0.3269,0.3649>。 可得 V(S2≥S1)=8.8404,V(S3≥S1)=7.2523。 根据式(4),有 P1=1,P2=8.8404,P3=7.2523。 通过归一化处理,可得3个评价指标对总目标的权重: P=(0.0585,0.5172,0.4243)。 依此类推,逐级计算其他指标结果见表3。 5个评价要素(灵活机动能力,越障能力,快速机动能力,环境反应能力,环境感知能力)的得分: 表3 权重表 同理可得,自身机动能力和智能感应能力的得分别为 该平台的总得分: 以100分为满分,该平台的总体性能评价较低,从各评价指标的得分来看,其环境感知能力较弱。主要原因是,该平台的感知范围、模型的更新频率以及模型的计算精度较差,且智能感应能力在整个性能评价体系中占据的权重较大。在今后的研究开发中,应该针对平台的智能感应能力,尤其是平台的探测硬件和软件进行有重点的开发,进而提升作战平台的整体性能。 本文针对同一任务类型地面无人作战平台的自身机动能力和智能感应能力两个方面对其综合性能进行评价。基于灵活机动能力、越障能力、快速机动能力、环境感知能力和环境反应能力,建立了地面无人作战平台的综合性能评价指标体系,在此基础上利用可拓展的层次分析法确定了评价指标的权重,提出了平台的综合性能评价模型,并用实例检验了模型的有效性和可用性。3.3 对某一准则层的因素进行排序
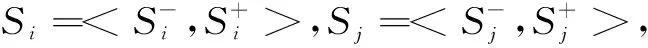
3.4 对所有准则层的因素进行排序

4 实例计算

4.1 指标权重的确定

4.2 各评价因素分数的确定
5 结束语
