基于任务逻辑和战位匹配的作战流程优化

尤俊郎,李胜勇,陈佳俊,宗思光

(海军工程大学,湖北武汉 430033)

作战任务逻辑是作战系统在不同态势下执行的动作流程,对指定的作战系统,在一定作战态势下,作战流程是固定的[1]。为缩短作战系统执行复杂作战任务时的时间,需要对其生成的作战流程进行优化。目前对作战流程优化的研究主要集中在对作战资源的管理、作战模型的构建和流程中节点的信息交互设计。文献[2]从军事需求的角度出发,描述模型之间的导入导出模块的接口关系,设计了基于平台运行的防空作战流程,给出了防空作战流程的模型验证方法; 文献[3]以UM建模方法为基础,以不确定环境作战为背景,研究了不确定作战环境因素对作战流程产生的影响;文献[4]通过提供一种基于规则的资源约束机制,实现舰艇编队防空作战过程中资源管理调度冲突的发现与解决;文献[5] 以DoDAF作战视图为研究工具,通过建模为新型驱逐舰防空武器系统顶层设计和风险控制提供技术支撑。

本文通过构建作战任务的逻辑模型,得到作战流程执行时间计算方法,根据战位——元任务匹配关系,得出所有的作战流程,通过对各流程执行时间和战位——元任务匹配关系分析,找到影响整个流程执行时间的关键节点,利用甘特图验证优化流程的可行性,最终选出最优流程,并得到实现最优流程的基本途径。

1 战位及元任务模型

战位即作战人员进行战斗活动的位置,这里是指具有完成作战任务的能力的战斗人员或战斗人员与装备的组合。战位主要根据作战需要,配备相应的装备和人员,通过人员操作装备来达到履行职责的目的[6]。战位模型主要包括战位名称或编号和可执行的任务。因此,战位可形式化为以下二元组:

Posj={ID,Opej}

式中，ID表示战位的编号,Opej表示战位Posj可执行的元任务集合。

作战任务是指在特定战场时空中,为达成作战目标而执行的作战行动集合。作战任务可按层次分解为若干层子任务,子任务可分解至元任务。其中子任务是作战流程的中间节点,元任务是作战任务的底层,不可再分解,通常是由战位直接执行的具体作战行动。作战流程是元任务有序执行的过程。元任务可形式化为三元组:

Opei={ID,Posj,tj-i}

式中，ID表示元任务的编号;tj-i表示元任务Opei由战位Posj执行时所需的时间值;Posj表示执行元任务Opei的战位。

2 作战任务逻辑模型构建

任务分解细化得到战位可执行的具体元任务,分解细化后的具体元任务不是离散孤立的,是存在逻辑关系关联的,这种逻辑关系确保了具体元任务的有序性,使得所有元任务的有序执行能够达到整个任务的完成。元任务之间的关系是一种横向的“兄弟”关系,集合Ope={ope1,ope2,…,open}中的元任务opei在行动执行的先后上表现为时序关系,包括顺序关系中的连续、间歇关系,以及在行动成败对任务成败的影响上表现为逻辑关系,包括与、或、选择、异或关系。综合考虑这两类关系,得到作战行动间的时序逻辑关系。元任务执行时序逻辑描述可采用统筹图形式进行描述,如图1所示。图中节点即元任务,图中的链接即元任务间序列关系。

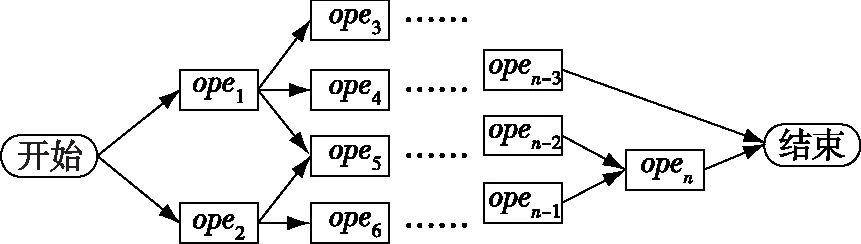
图1 任务统筹示意图

元任务的时序转换主要有四种情况:“一对一”、“一对多”、“多对一”和“多对多”四种情况[7]:

1) “一对一”的情况,即opei的下一节点只有opej,且opej的上一节点也只有opei,则opei和opej为顺序与的关系,只有当opei与opej都执行成功时,这条路径才能继续向前推进,此时opei与opej为连续的逻辑关系。如图2所示。

图2 “一对一”示意图

在此情况下,从

ope

i

至

ope

j

的任务执行时间值按照以下公式计算:

t=ti+tj

2) “一对多”的情况,即opei的下一节点有多个元任务,而opej(j=1,2,3,4)的上一节点只有一个元任务。当opei执行完毕后,opej(j=1,2,3,4)中所有元任务都开始执行,则opej(j=1,2,3,4)中各任务间为并发与的逻辑关系。如图3所示。

图3 “一对多”示意图

当opej(j=1,2,3,4)中各元任务间为并发与的逻辑关系时,opej(j=1,2,3,4)中各任务开始时间不存在先后顺序,则tj的大小取决于opej(j=1,2,3,4)中执行时间最长的任务,因此,从opei至opej的任务执行时间值按照以下公式计算:

t=ti+tj=ti+max(t1,t2,t3,t4)

3) “多对一”的情况,即opej的上一节点有多个元任务,而opei(i=1,2,3,4)的下一节点只有一个元任务。当opei(i=1,2,3,4)中只要有一个元任务执行成功,其他任务中止执行,立即执行opej时,opei(i=1,2,3,4)中各元任务是异或关系。当opei(i=1,2,3,4)中所有任务必须全部执行完毕后,才能执行opej时,opei(i=1,2,3,4)中各元任务是与关系。如图4所示。

图4 “多对一”示意图

当opei(i=1,2,3,4)中各元任务间为异或的逻辑关系时,则ti的大小取决于opei(i=1,2,3,4)中执行时间最短的任务,因此,从opei至opej的任务执行时间值按照以下公式计算:

t=ti+tj=tj+min(t1,t2,t3,t4)

当opei(i=1,2,3,4)中各任务间为与的逻辑关系时,则ti的大小取决于opei(i=1,2,3,4)中执行时间最长的任务,因此,从opei至opej的任务执行时间值按照以下公式计算:

t=ti+tj=tj+max(t1,t2,t3,t4)

4) “多对多”的情况,即opei(i=1,2)的下一节点有多个元任务,而opej(j=3,4)的上一节点也有多个元任务。当ope1和ope3或ope2和ope4执行成功时,ope2和ope4或ope1和ope3不需要执行,路径即可向前推进,且当ope1和ope4或ope2和ope3执行成功时,ope2和ope3或ope1和ope4不需要执行,路径即可向前推进,则此时opei和opej中各任务之间为选择的逻辑关系;否则可以将其分解为“一对多”和“多对一”的组合。如图5所示。

图5 “多对多”示意图

当opei和opej中各任务之间为选择的逻辑关系时,则ti的大小取决于opei(i=1,2)中执行时间最短的任务,则tj的大小取决于opej(i=3,4)中执行时间最短的任务,因此,从opei至opej的任务执行时间值按照以下公式计算:

t=ti+tj=min(t1,t2)+min(t3,t4)

综上所述,完整作战任务流程中元任务之间的关系不外乎以上4中情况,在已知各元任务执行所需时间和元任务间逻辑关系的基础上,不难求出整个作战流程完成所需的时间T。在实际作战中,不同的战位执行同一元任务对整个作战流程具有不同的影响,因此,可以将战位作为变量对作战流程进行灵敏度分析,并利用计算软件完成所有组合的穷举,生成甘特图。为确保流程的合理性,需排除不符合实际的情况,排除条件为实际作战过程中的规则和条令,如:一个战位不能同时执行两个元任务,以此选择该流程的最优路径,实现流程的优化。由于实际作战中作战流程具有特殊性,各元任务之间逻辑关系相对固定,因此作战流程优

化的求解主要通过示例来说明。

3 战位-元任务的匹配

战位-元任务的匹配是指战位与元任务的关联,即任务分解得到的元任务由什么战位来执行。匹配关系通过战位功能建立了元任务集合与战位之间的映射关系,战位是功能的提供方,元任务是功能的需求方。战位与元任务一般是一对一的映射关系,即每个战位负责本战位主要作战任务,但在实际作战中,为提高作战系统的抗毁伤性和稳定性,往往会为作战流程中的关键任务节点预备具有复用功能的战位,当执行该任务的主要战位发生故障或被摧毁后,复用战位在空闲状态下能够替代主要战位执行该任务,从而确保作战流程顺利向前推进,此时战位与元任务时一对多的映射关系,即一个战位可以执行多个元任务。

4 作战流程优化

本文创建一个15个元任务节点的作战流程进行分析计算,流程如图6所示。

图6 作战流程示例

在该作战流程中,共有15个战位执行以上15个元任务,战位-元任务匹配如表1所示。

表1 战位-元任务匹配表

对作战流程进行分解,得出2条分路径，如图7、8所示。

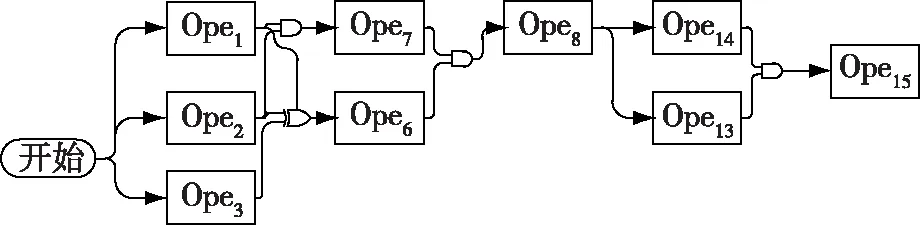
图7分路径A

由以上路径可得分流程A的执行时间TA:

TA=max((min(t1,t2,t3)+t6),(max(t1,t2)+t7))+t8+max(t13,t14)+t15

(1)

图8 分路径B

由以上路径可得分流程B的执行时间TB:

TB=max(t3,t4)+t5+min((min(t9,t10)+t12),(max(t9,t10)+t11))+t15

(2)

可得,总流程T的执行时间:

T=TA+TB=min(TA,TB)

(3)

将表1中数值代入式(3)中,通过Matlab软件计算出总时间T,可得表2。

表2 作战流程全举表

从表2可得,未经优化的作战流程执行总时间T=31,甘特图如图9所示。

图9 未优化作战流程甘特图

从表2可知,作战流程执行总时间最短为T=29.7,这四种情况中,元任务Ope6由战位Pos4执行,元任务Ope8由战位Pos5执行,元任务Ope9由战位Pos6或Pos9执行,元任务Ope10由战位Pos7或Pos10执行,共有以下四种情况:

流程标号13:元任务Ope9由战位Pos6执行,元任务Ope10由战位Pos7执行，如图10所示。

流程标号14:元任务Ope9由战位Pos6执行,元任务Ope10由战位Pos10执行，如图11所示。

流程标号15:元任务Ope9由战位Pos9执行,元任务Ope10由战位Pos7执行，如图12所示。

流程标号16:元任务Ope9由战位Pos9执行,元任务Ope10由战位Pos10执行，如图13所示。

图10 作战流程甘特图(流程编号13)

图11 作战流程甘特图(流程编号14)

图12 作战流程甘特图(流程编号15)

图13 作战流程甘特图(流程编号16)

从以上四种选优结果可知,元任务Ope5和Ope8是整个作战流程中的关键节点,这两个元任务都是承接上下阶段任务的单节点,它们的执行时间直接影响了整个作战流程的执行时间,而且在实际作战中,由于单个战位不可能同时执行两个以上的作战任务,因此以上选优结果在实际中不能实现,即元任务Ope8必须由战位Pos8来执行。由表2可知,当元任务Ope8由战位Pos8来执行,且元任务Ope10由战位Pos7来执行时,可以实现作战流程的优化,即编号为2、4、10、12的流程为优化后的流程。

从以上选优过程可以看出:通过作战任务逻辑模型的构建,寻找出影响作战流程执行时间的关键节点,通过调配作战能力更强的战位来执行关键节点元任务或提升战位执行关键节点元任务的能力,可以缩短作战流程的执行时间,最终实现作战流程的优化。如在上例中,可以通过提高战位Pos5的作战效能,缩短战位Pos5执行元任务Ope5的时间,使元任务Ope5的结束时间小于元任务Ope8的开始时间,最终实现最优作战流程。提升作战任务执行效能的核心途径是人员装备的有效结合,但在装备确定的情况下,作战人员将会是影响作战任务执行效能的主要因素,因此在军事活动中,提升作战能力的主要途径就是提高战位人员的操作熟练程度,强化作战人员完成任务的能力。

5 结束语

本文通过构建作战任务逻辑模型,计算出作战流程的执行总时间,并通过战位与元任务匹配关系调配,找出影响作战流程执行总时间的关键节点,在作战流程相对简单的情况下能够实现最优作战流程的遴选,并为缩短流程时间提供初步的实现途径。但是，作战过程中元任务间逻辑关系更为复杂,不仅需要满足作战流程的减时需求,而且要考虑实际作战过程中战位执行任务成功率和作战装备技术性能发挥的不确定性对作战任务的影响,还需找到更加合理的算法,使其更贴近作战过程实际。