动力定位预测控制器船舶模型试验研究

， ， ，，

(中国船舶科学研究中心，江苏 无锡 214082)

0 引言

动力定位系统主要包括测量系统、控制系统以及推进系统，其中控制系统是动力定位系统的核心。其原理是按照测量系统测得的船舶当前位置与设定位置之间的偏差，以一定的控制方法计算出船舶到达设定位置所需的推进器推力和力矩，再通过推进系统中的推力分配算法将计算的推进器推力合理的分配到船舶各个推进器上。对于实际的船舶控制，由于模型参数的时变性以及环境力的影响，再加上船舶控制中的各种约束条件，动力定位系统对于船舶的控制会产生超调现象，控制效果并不令人满意，对于约束条件较为苛刻的工程应用来说危险性极大。为了解决模型参数以及环境力影响的问题，业界学者也提出了包括自适应模型参数或者控制参数整定[1-2]、非线性模型[3-4]以及模拟环境力前馈[5]等方式来解决。然而这种控制方式无法确保对船舶的控制满足理论约束。

本文中控制系统使用的是预测控制理论。预测控制起源于工业生产过程当中，一般具有三个基本特征分别为：预测模型、滚动优化、反馈校正。工业生产过程当中所控制的对象大都具有非线性和多约束的特点，和船舶的控制特性类似；同时，预测控制对船舶的运动可以作短时的预测，通过在滚动优化中增加约束条件，可以同时保证控制结果的最优性和约束性。因此，将预测控制应用于动力定位控制器的设计有着极大的优越性。

国内对于动力定位预测控制器已经有了不少的研究，比如说王元慧[6]、钱小斌[7]、苏义鑫[8]等人，但是这些研究大都只是停留在算法仿真阶段，由于仿真是在一种充分理想的状态和环境下进行的，仿真算法的实用性和有效性有待获得模型试验的验证。本文针对仿真条件的不足利用仿真算法设计了船舶模型试验。

1 动力定位预测控制器设计

传统的预测控制器使用的是不变的预测模型，然后直接补偿的方式进行反馈校正。然而，在实际动力定位预测控制器的设计中，考虑到船舶运动时参数的时变性，设计了如下图所示的预测控制器。

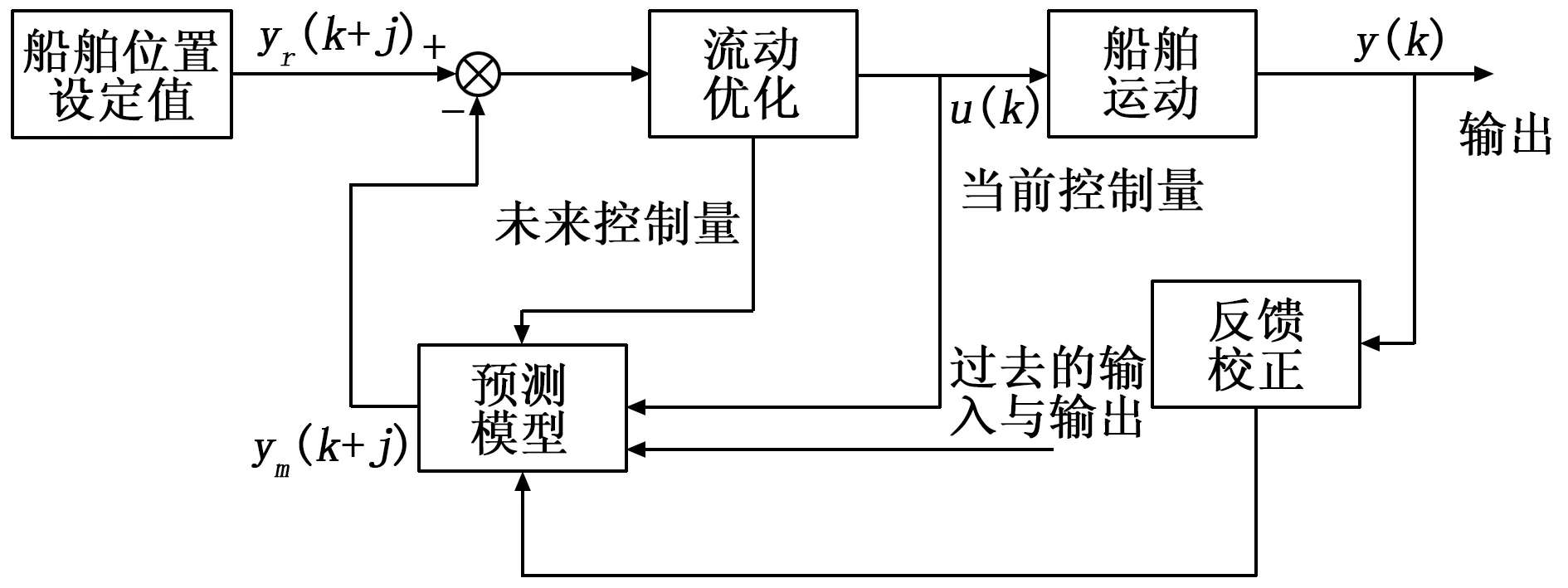
图1 广义预测控制器结构图

1.1 预测模型

由于船舶参数的时变性，在控制器的设计当中，我们选取了参数较少的受控自回归滑动积分平均模型(CARIMA)作为预测模型[9]。该预测模型的一般结构为：

A(z-1)y(k)=z-dB(z-1)u(k)+C(z-1)ξ(k)/Δ

(1)

其中：A(z-1)=1+a1z-1+a2z-2+...+anaz-na,B(z-1)=b0+b1z-1+b2z-2+...+bnbz-nb，ξ(k)为白噪声，Δ=1-z-1作为差分环节，一般假设系统延时d=1，C(z-1)=1。

为了得到船舶k+j时刻的运动预测值，将下列多番图方程带入式(1):

(2)

可得:

y(k+j)=Fj(z-1)y(k)+Gj(z-1)Δu(k+j-1)+

Hj(z-1)Δu(k-1)+Ej(z-1)ξ(k+j)

(3)

如此，我们可以得到船舶j时刻的位置与过去的船舶位置和推进力之间的关系，可以证明用多番图方程获得的船舶未来时刻的位置估计是最优的[10]。

用CARIMA模型获得的船舶运动预测模型结构简单，参数较少，更加方便参数的辨识；这种结构摒弃的传统预测控制算法中的多阶矩阵迭代，由此减少了算法计算量，提高了算法的实时性；模型结构中包含了船模的过去的输入输出参数，可以将环境力的影响以及船舶推进器的效率问题都包含在船舶的运动模型当中，使得整个系统鲁棒性更好。

1.2 滚动优化

滚动优化主要是用来计算最优推进力和力矩。由于在预测模型中获得的船舶位置预测值是一个和未来船舶推进力有关的代数式，需要在滚动优化中以一定的性能指标计算出最优推进力。

一般预测控制中滚动优化的性能指标函数都是以预测的船舶位置与设定的目标位置之间的偏差最小以及船舶到达目标位置所使用的推进器推力最小设定的，其性能指标函数如下:

(4)

通过对此性能指标函数施加一系列约束比如位置约束、速度约束以及推进器推力(变化)约束，求得一组最优推进力。将每次求得的一组最优推进力的第一项作为当前时刻船舶的最优推进力。在仿真过程中发现，采用这种形式的性能指标函数并不能充分的利用推进器推力，而且对于速度进行过小的约束，必然就减小了动力定位系统的控制效率。考虑到以上因素，在该控制器中对传统的性能指标函数进行了修改，在原有的基础上加入了位置微分项，和PID控制的微分参数功能类似，这种方式使位置偏差项和船模速度项在船模向设定位置运动的过程中各占权重；与PID控制不同的是，这种方式利用了预测控制中对船舶位置的预测，因而对船舶的控制不会存在滞后现象。修改后的性能指标函数如下:

(5)

1.3 反馈校正

由于船舶运动时阻尼和附加质量的时变性，实际控制中环境力的慢变性，因而在本预测控制器设计中采用的是递推最小二乘法来对预测模型参数进行更新[11]。将船舶三自由度运动分别研究，单自由度的预测模型可以写成如下形式:

y(k)=-a1y(k-1)-...-anay(k-na)+

b0u(k-1)+...+bnbu(k-1-nb)+ξ(k)=

φT(k)θ+ξ(k)

(6)

其中:

(7)

随着时间的增长，采用最小二乘法会产生数据饱和的现象，而且对于船舶的非线性运动，船舶过去的输入输出对现在的船舶模型参数参考意义不大，因此在反馈校正中选择带遗忘因子的递推最小二乘法来加强新数据对船舶参数的影响。具体步骤如下:

(8)

这种递推的方式的实质是将船舶的非线性运动局部线性化，然后用线性系统的控制方法来控制船舶运动。

2 试验装置与试验方法

本次模型试验的设备主要有带棱镜的全站仪一台，自主设计的带操纵杆的中控机一台，笔记本电脑一台，其关系如图2所示。

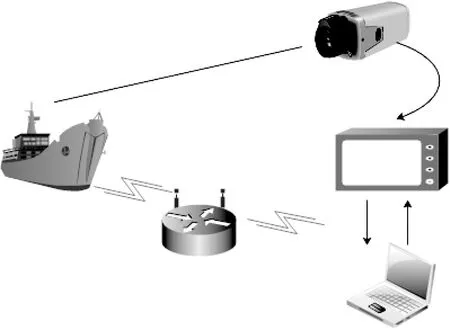
图2 试验机构原理图

本次模型试验使用的船舶模型是一艘航标船模型，其结构如图所示。该船舶模型有一个槽道推进器(艏部)和一对全回转推进器(艉部)，其质量矩阵和阻尼矩阵分别为:

(9)

图3 试验用船舶模型

全站仪是本次试验的位置测量仪器，其测量的位置是相对于以自身为原点，平行于水池边的方向为Y轴，垂直于水池边的方向为X轴确定坐标系下的坐标。通过发射激光并接受安装在船舶重心上的棱镜的反射解算船模的当前位置，其位置测量精度可达1 mm。船体坐标系是以船模的重心位置为原点，艏向方向为y轴，横向方向为x轴。

中控机使用的是本试验室自主研制的动力定位人工操作台，该操作台集成了动力定位系统的所有功能，既可以选择使用内部控制算法或者外部算法进行自动控制，也可以通过台面上的操纵杆进行手动控制。本次试验中为了防止模型失控，保证设备安全，选用外部计算机作为进行控制算法运算的同时，保留了自动手动切换功能。

笔记本电脑上面运行的是本次试验的控制算法。试验中需要嵌入中控机的必须是基于LabVIEW环境下的可执行文件，试验前，通过LabVIEW中的Matlabscript控件，我们将Matlab语句整个移植到LabVIEW中，并加入了数据采集以及控制量显示功能。整个控制流程如图4所示。

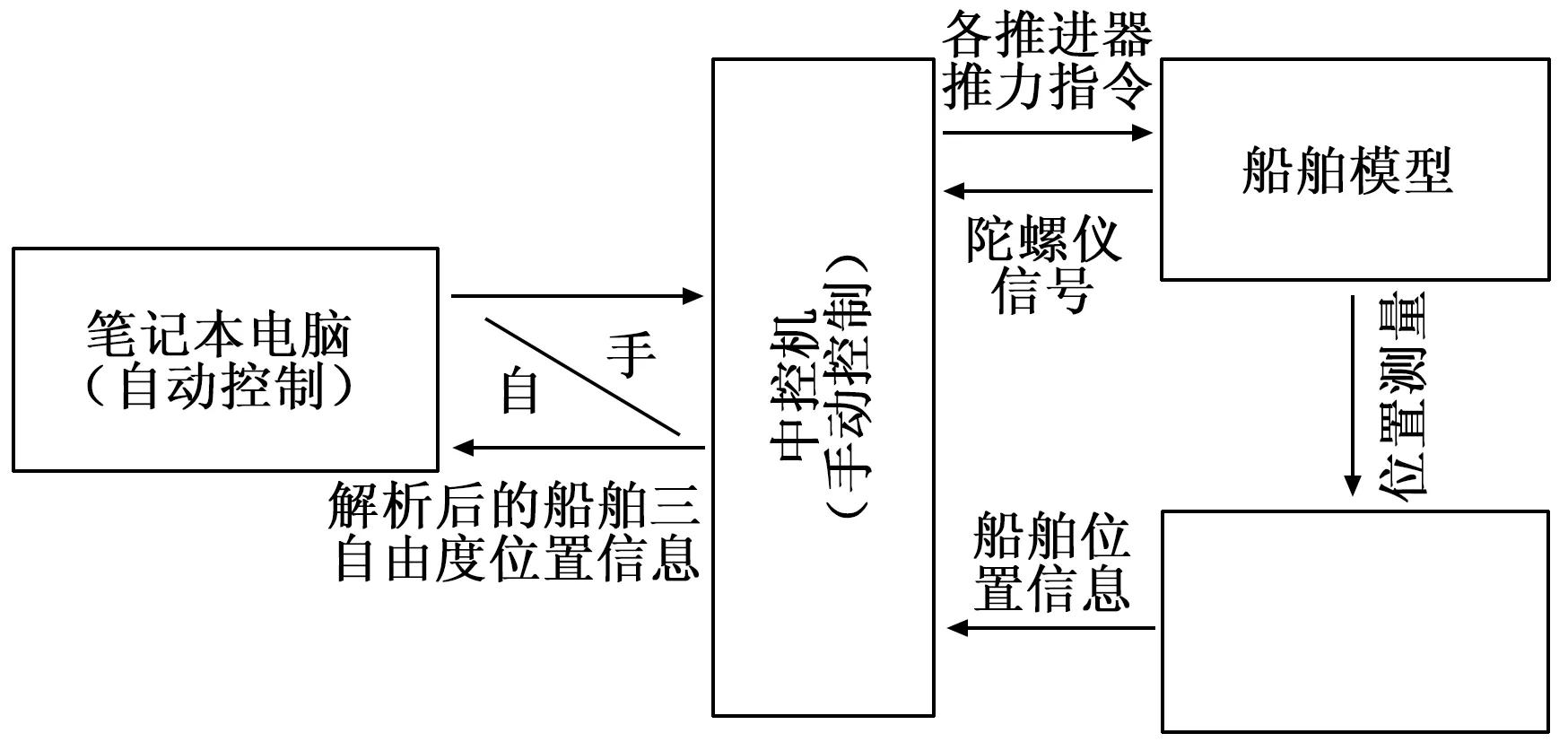
图4 控制流程图

全站仪和陀螺仪将测量信号发给中控机进行数据解析，中控机将解析后的数据发送给笔记本电脑进行控制运算，笔记本电脑将计算好的推力数据发送给中控机进行推力分配，中控机将分配好的推进力以指令的形式发送给船模。船模与中控机之间通过无线路由器连接，其他设备之间都是有线直连。

3 船舶模型试验与结果分析

按照仿真中设置的系统参数，滚动优化中的性能指标函数中位置偏差权值三自由度都为0.5，位置变化权值船舶x、y方向的权值设置为40、艏向方向为60；反馈校正中的遗忘因子设置为0.97。根据螺旋桨的所能产生的最大推力以及船模主要参数，我们将船舶的推力和力矩约束分别设置成了±10 N和±10 N·m，每次推力和力矩的变化设置成了±1 N和±1 N·m。

为了方便研究预测控制器控制参数与船舶各自由度运动之间的关系，采用控制变量法设置了下列一组试验，船模x方向的位置变化为2 m～0 m～2 m～2 m，船模y方向的位置变化为-8 m～10 m～10 m～7 m，船模的艏向角度变化为80°～50°～50°～50°。船模从初始位置到第一目标位置三自由度位置同时改变；从第一目标位置到第二目标位置是仅改变船舶x方向位置；从第二目标位置到第三目标位置是仅改变船舶y方向位置。试验结果如图5所示。

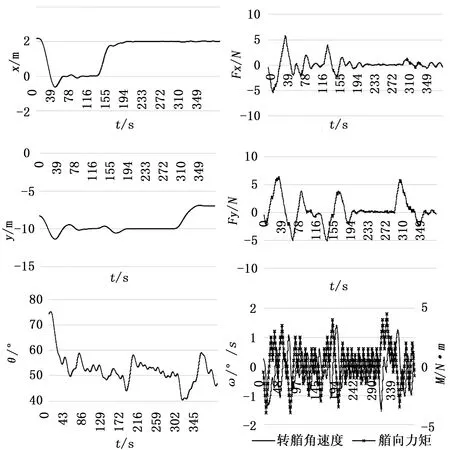
图5 船舶模型三自由度运动轨迹及最优推进力图

从试验结果可以看出，第一阶段，船舶三个自由度位置同时改变时，对船舶x方向和y方向位置的控制都不同程度出现超调，到达稳态的调节时间较长，船舶艏向角度偏离目标位置处于震荡状态，稳态误差较大；第二阶段，仅改变船舶x方向位置时，对于船舶y方向位置以及艏向位置的影响都相对较小，船模的艏向角度仍然处于震荡状态；第三阶段，仅改变船舶y方向的位置时，对船舶x方向位置的控制无影响，而却使得船舶的艏向角度在其目标位置附近产生了大幅的波动，直到船舶y方向的位置趋于稳定，船模艏向角度大幅波动的现象才得到有效的减缓，但是波动的状态仍然在持续。

总结上述的船模运动特征主要有如下几点：第一，船模艏向角度一直处于不稳定状态；第二船模y方向的运动或者艏向角度的改变会对对方的运动造成比较大的影响。针对艏向角度控制不稳定，首先考虑的就是艏向角度的控制参数设置的过小，从而控制中计算性能指标函数的最优解时所得到的最优解并不能使艏向角度维持现状；而船模y方向运动对船模艏向角度的影响，我将其归结于船舶横荡和艏摇的耦合现象，由于在算法中去除了横荡和艏摇的耦合项，因此，不能消除船模运动中耦合现象的实际影响。

为了提高对船舶艏向角度的控制效果以及减小耦合现象对船舶运动的影响，在滚动优化中将位置偏差权值0.5(x方向)，4(y方向)，4(艏向)，位置变化权值80(x方向)，100(y方向),100(艏向)。在改变控制参数之后，又进行了下面一组试验，船模x方向变化为-2 m～0 m，船模y方向变化为-10 m～8 m，船模艏向角度变化为40°～50°，试验结果如图6所示。

图6 改参数后船舶模型三自由度运动轨迹及最优推进力图

改变参数后，船模最终到达其指定位置，但是由于船模x方向位置偏差权值相对较小，因而船模x方向的到达指定位置的过程时间偏长；船模横荡和艏摇的耦合现象有了一定的改善，但是耦合现象仍然存在，由于增大了艏向角度变化权值，艏向角度的波动幅值得到有效减小。即使如此，改变参数后的控制算法对于船舶位置的控制效果有了极大的改善，艏向角度的稳态误差也进一步减小。

4 结束语

本文针对现有动力定位算法缺少模型试验支撑的现状，通过船舶模型试验验证了所涉及控制算法的有效性。试验中根据船舶的运动情况对控制参数的修改使得船舶模型的运动基本达到预计要求，具有一定的工程实践意义。然而，从试验中标还是显示出一系列亟待解决的问题：由于船舶横荡和艏摇之间的耦合对船舶的控制影响比较大，其一就是解决船舶运动时必然存在的运动耦合问题；其次控制算法中两组控制参数(位置和速度)之间时相互影响的，如何选择合理的控制参数，寻求控制效果和控制时效之间的平衡也是后期研究中需要重点探讨的；再者由于本次试验只是静水试验，基本不存在环境力干扰的问题有环境力干扰时算法的实际控制还有待检验。