基于惯导/数据链的动态相对定位方法

,,

(卫星导航系统与装备技术国家重点实验室，石家庄 050081)

0 引言

无人机通过机间信息交互实现机间信息共享，进行无人机共同执行任务，并且增加无人机探索方式，实现资源优化配置，从而有效提高无人机工作性能[1]。无人机协同工作时，需要互相了解各自的相对位置情况，因此高精度的无人机相对定位是无人机机间协作的前提[2]。

目前对于无人机协同工作，可通过卫星导航系统得到各个无人机间的绝对位置，从而获得无人机间的相对位置信息，达到无人机机间相对定位的目的[3]。但是，随着现代科技技术的飞速发展，电子信号干扰技术发展迅速，而卫星导航系统传输链路脆弱易受欺骗干扰，在复杂干扰环境下依靠卫星导航系统进行导航定位的无人机协同工作模式已经不能得到可靠地保障。找到一种复杂环境下可靠的导航定位方法尤为重要。惯性导航系统是一种隐蔽的自主导航系统，通过无人机自身惯导信息也可以获得无人机间相对位置关系，但是惯性导航系统存在误差随时间累积的问题，长时间工作情况下定位精度不能保障[4]。数据链同样具有很强的抗干扰能力，并且可以满足复杂环境下的无人机之间的通信与测距功能[5]。针对上述问题，将机间测距与惯性导航系统结合使用，提出一种可以实现复杂环境下适用于高运动状态的机间相对定位算法，实现复杂环境下可靠的相对定位能力。该方法可在卫星导航系统不可用时作为应急备份导航系统。

1 机间惯导/数据链协同定位原理

惯导系统的定位误差呈正态分布，并且惯导定位误差随时间积累。为每架无人机装备高精度测距数据链，用来进行无人机间实时相互测距，并传输无人机之间惯性导航系统输出的信息和无人机之间的测距信息[6]。通过机间惯性导航系统提供的现在时刻和前两个时刻的速度信息与数据链测距信息协同建立最小二乘相对定位方程，估计出无人机间相对位置信息。以数据链测距值与最小二乘相对定位结果的差值作为观测量，通过秩亏网平差算法对相对定位误差进行估计，进一步修正相对定位结果。

1.1 机间协同相对定位原理

在动态条件下无人机相对运动时，可将无人机间相对位置变化看作由无人机相对运动速度引起的伪距变化，无人机运动在足够短时间内将无人机相对速度矢量在机间相对位置矢量上的投影作为无人机相对矢量的变化。因此，进行惯导数据链协同相对定位时，由惯导系统输出的速度信息得到机间近似伪距变化率，将数据链测距值作为机间伪距真值，由此建立惯导速度与数据测距值间的数学关系式。具体推导过程如下。

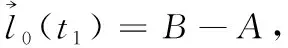
(1)

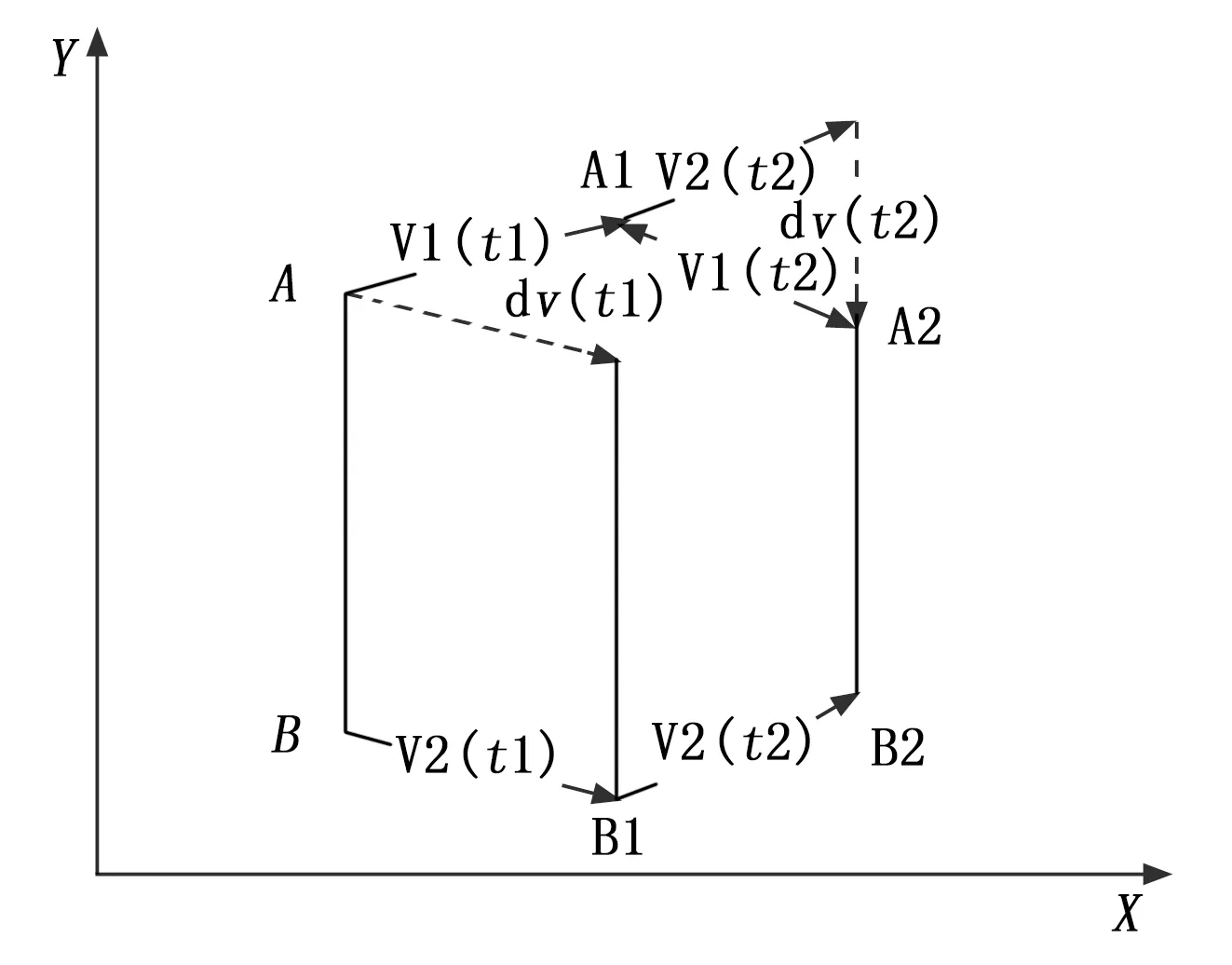
图1 相对位置关系示意图

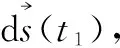
(2)

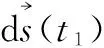
1.2 机间测距原理

对于集群飞行器，由于机间数据链信号传播距离短，并且可采用点波束等形式进一步加强接收功率，因此相对于卫星导航信号，在干扰环境下机间数据链具有更高的抗干扰能力，适用于在复杂环境下无人机获取机间观测量信息。通过数据链进行机间测距并利用数据链通信将无人机间的测距信息和惯导系统输出的信息在无人机间进行交互。

机间数据链测距是通过机间发射无线电信号进行测距，无线电测距的实现包括单向单程测距、双向双程测距和双向单程测距。由于单向单程测距方法实现全局同步需要高精度晶振，代价高昂。双向双程测距方法，需要以相应的次序进行无人机机间测距，这种测距方法不能实现高速实时测距能力，并且这种测距方法的设备组成较为复杂。基于上述原因，针对机间测距本文采用一种非相干无线电测距方法——双向单程测距方法[8]。

采用双向单程测距方法，无人机之间可通过通信获得各无人机间时钟不同步值得方法，实现无人机间时间同步。因此，每个无人机只需要有自己的时钟即可，并且每个无人机在接收其他无人机的测距信号时，同时发送测距信号，这种测距方法，不需要复杂的设备，并且能够进行高速实时的测距，具体测距算法如下。

无人机i通过数据链向其他无人机发送测距信号，并且接收其他无人机传送来的测距信号。假设无人机间测得的测距信号传输时间为tij，两无人机之间的时钟差异为Δtij，无人机i接收到的测距信号时间为，无人机j接收到的测距信号时间为，则可得以下关系式：

T1=tij+Δtij

(2)

T2=tij-Δtij

(3)

则由式(2)和(3)计算得:

(4)

(5)

通过以上公式可知，机间测距值可通过机间测距信号传播时间乘机间测距信号传输速率得到。由此可以看出，双向单程测距既可以实现机间信息传递，又可以实现机间测距，并解决了机间时钟不统一的问题。

2 机间相对定位模型与算法

机间惯导误差对数据链信号观测的影响表现为由相对速度误差引起的多普勒误差和由相对位置误差引起的伪距误差[9]。设无人机搭载的惯导系统误差近似一致，利用机间数据链进行测距，并与惯导输出的信息建立机间相对定位方程，估计机间相对定位误差。针对方程的求解，提出最小二乘相对定位算法。

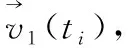
(6)

t2，t3时刻两节点间相对位置分别由两点在空间中的相对速度对时间进行积分可近似为t2，t3时刻两点间相对位置空间矢量。

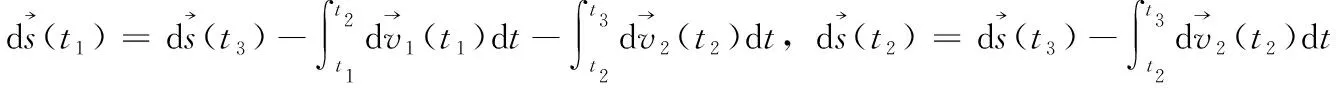
(7)

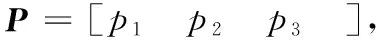
则可得到机间相对定位方程为：

GX=P

(8)

X=(GTG)-1GTP

(9)

由于最小二乘相对定位算法是基于机间相对速度在机间相对位置矢量上投影的运算，相对定位运算时间是瞬时而不是周期内伪距变化，相对定位时间频率越低，等效于伪距差观测的误差越大，时间频率越高，越接近于多普勒变化，得到的相对定位结果误差越小[10]。

利用最小二乘法求解出的机间相对定位结果仍然存在一定误差，通过最小二乘相对定位结果与机间数据链测距值为基础建立秩亏网平差误差方程，来估计机间相对定位误差，对最小二乘相对定位结果进行修正，从而将机间相对定位精度提高到更高水平[11]。

由于惯导定位误差呈现出正态分布，并且多套惯性导航系统使用在同一平台，通过将惯导输出值进行加权平均可以减少惯性导航系统定位误差，国外在高价值有人机应用中有所研究，但对于载荷、成本有限的小型化无人机，搭载多套惯导系统并不现实，因此将加权平均的思想引用到无人机集群中。由无人机间惯导系统提供的速度信息计算得到的无人机间距离和利用数据链测距得到的测距值之差作为量测量，结合测绘平差中秩亏自由网平差算法，来估计计算得到的无人机之间相对位置误差，实现无人机集群相对定位误差精度的提高。机间相对定位误差模型及秩亏自由网平差校正算法如下。

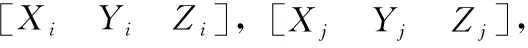
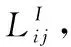
(10)

(11)

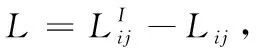
(12)

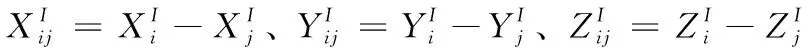
设代求参数向量为x=[δxij,δyij,δzij]T，将式(12)写成矩阵形式为:

L=Bx+Δ

(13)

由于机间相对定位中各个节点坐标均为待定点，上述方程起算数据不足，缺乏必要起算点，并且系数矩阵为秩亏矩阵，在计算时结合测量平差理论，利用秩亏网平差算法进行计算。

V=Bx-L

(14)

式中，V为Δ估计值，L为观测值，B为系数矩阵。

由于系数矩阵B为奇异矩阵，利用最小二乘准则得到法方程为：

Nx=W

(15)

式中，N=BTPB，W=BTPL，由于系数矩阵B为秩亏矩阵，法方程系数矩阵N也为奇异矩阵，法方程解不唯一。为了得到相对定位误差参数的唯一解，由最小二乘最小范数准则，xTPxx=min得最小范数解：

(16)

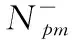
3 仿真分析

仿真条件设置如下：两架无人机分别编号为1、2；无人机1初始位置坐标为[100,100,100]，初始速度为200 m/s；无人机2初始位置坐标为[1,1,100]，初始速度为200 m/s；机载数据链传输无人机间的相互测距值，机间数据链测距精度为1 m；无人机均装载相同精度的惯性导航系统，陀螺随机常值漂移为0.01°/h。相对定位的计算周期为1 s。在仿真中认为无人机装备的惯性导航系统均为同精度，在仿真计算中取等权值，仿真计算流程如图2所示。

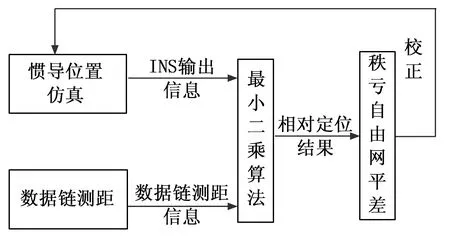
图2 机间惯导数据链相对定位仿真流程图

仿真结果如图3和图4所示。图3是机间惯导数据链协同相对定位结果。图4是机间惯导/数据链相对定位误差结果。

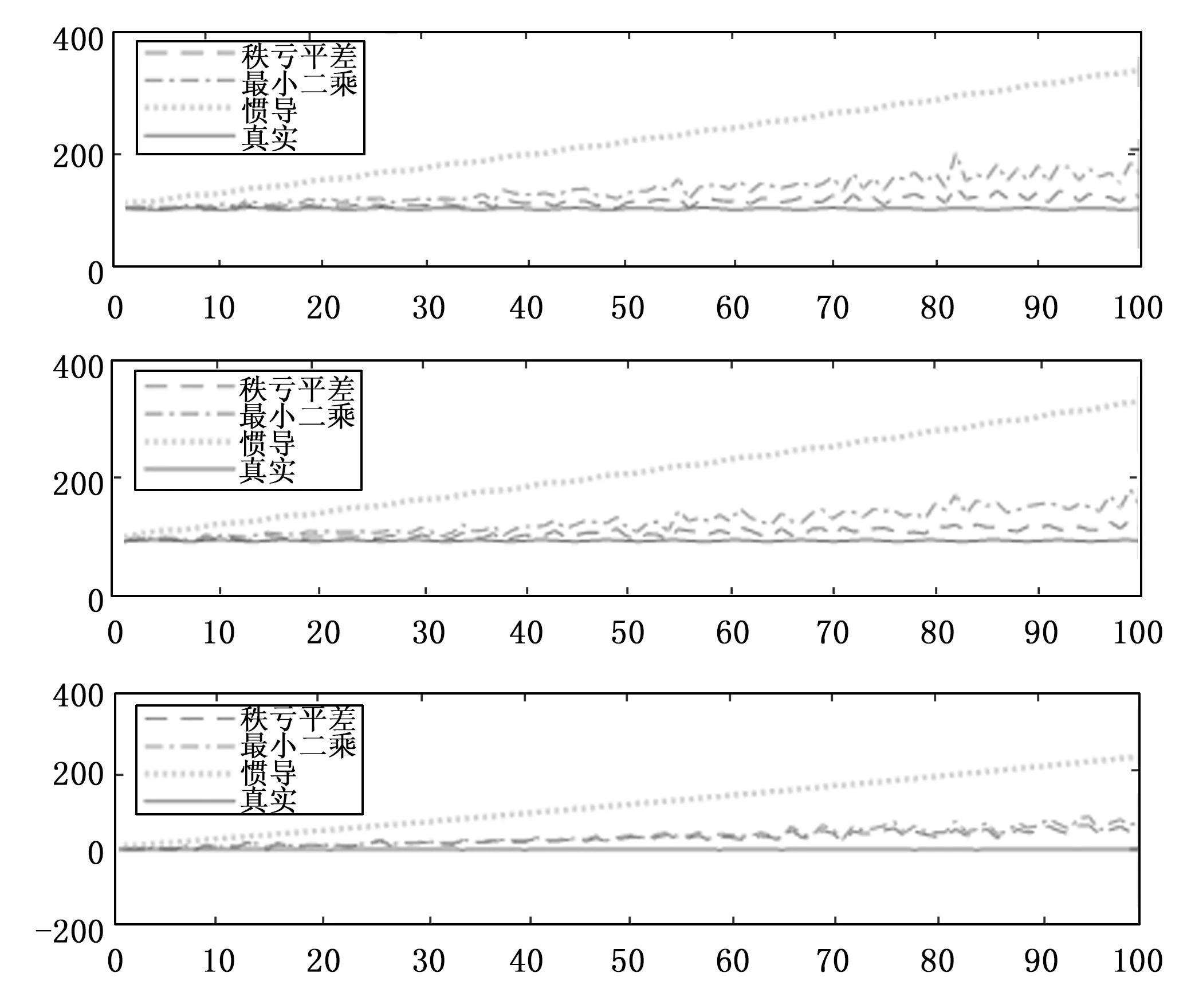
图3 相对定位结果

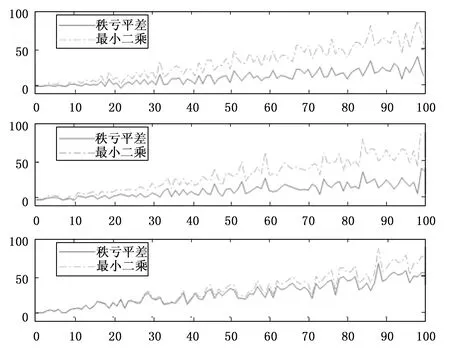
图4 相对定位误差

图3中点虚线表示由惯导系统输出的相对定位结果，点横线表示由最小二乘相对定位方法得到的相对定位结果，短虚线表示经过秩亏网平差算法修正后得到相对定位结果，实线表示无人机之间实际相对定位结并且果。从图3中可以看出，通过最小二乘相对定位方法将惯性导航系统的相对定位发散速度降低，同时提高了相对定位精度。利用秩亏网平差算法对最小二乘相对定位结果进行校正使相对定位结果发散速度趋于平稳，使相对定位结果更接近真实情况。

图4中虚线为最小二乘相对定位误差曲线，实线为秩亏网平差校正后相对定位误差曲线。从图中可以看出，通过秩亏网平差算法降低了最小二乘相对定位误差发散速度，并提高了相对定位精度。

从表1中可以看出，惯导系统在100 s内的相对定位统计误差为346.87 m，通过最小二乘算法得到的相对定位结果统计误差为104.51 m，将惯导系统相对定位精度提高了3.32倍。再经过秩亏网平差算法对相对定位结果的校正，相对定位统计误差为43.91 m，将最小二乘相对定位精度提高了2.38倍。综上所述，通过惯导数据链协同定位算法，将惯导系统相对定位精度提高了7.89倍。

表1 相对定位统计误差

4 结论

针对复杂环境下无人机协同执行任务能力，提出了通过机间数据相互测距的距离信息与惯导信息结合的无人机机间相对定位系统，可以实现无人机间两点相对定位，通过最小二乘定位算法有效延缓了惯导位置误差发散速度，并且通过秩亏自由网平差算法实现了惯导信息相对位置误差的修正，将机间动态相对定位精度提高到原来的7.89倍。基于惯导/数据链的动态相对定位算法解决了纯惯导条件下的单链路惯导协同相对定位问题。并且基于机间数据链与惯导结合的机间动态相对定位系统，具有很强的抗干扰能力，在卫星导航系统不可用时，可作为应急备份导航系统。

本文提出的基于最小二乘的相对定位算法具有线性误差，使用最小二乘相对定位算法需要无人机间具有很高的相对运动状态，对于运动平稳的情况得到的相对定位结果误差较大。秩亏网平差算法解决了系数矩阵秩亏问题，但是在两点间惯导协同相对定位中具有一定局限性，秩亏网平差算法在有多个节点的网络，具有多个修正参考值，对于相对定位误差修正更加准确，因此本文提出的机间惯导数据链协同相对定位算法，可以应用到无人机集群网络中，通过加权秩亏网平差算法实现无人机集群的相对定位。