改进的等权值抗混淆算法

,燕威,

(1.中国民航大学 职业技术学院，天津 300300；2.中国民航大学 电子信息与自动化学院，天津 300300)

0 引言

在20世纪70年代中期，电路板的测试是通过在线测试进行的，表面贴装技术对板上互连测试造成了更大的困难。为了找到解决测试问题的方案，一批科学家在1980年中组建联合测试行动小组(JTAG)。1990年，JTAG推出了基于边界扫描的测试技术，被称为IEEE1149.1标准[1]。边界扫描技术的发展带动了边界扫描算法的而不断的发展。

目前国内外相关的边界扫描测试算法很多，各有其优缺点，通常可分为三类，第一类是采用无限制短路故障模型的常规测试算法，第二类是采用有限制短路故障模型的结构测试算法，第三类是利用测试过程中所获取的信息对测试向量集进行优化的自适应算法[2]。本文在分析了常规测试算法等权值互连测试算法的基础上，将结构测试算法的思想应用到等权值算法上，提出了基于有限制短路故障关系的改进等权值互连测试算法。

1 等权值算法

1.1 等权值算法概述

1.2 等权值算法分析

抗误判定理[4]：权值为W的一个固定权值诊断算法的测试集(Matrix of Test Vectors，MTV)是一个独立的贯序测试向量(Sequential Test Vector,STVs)矩阵。

推论[4]：由独立STVs组成的测试集MTV对如下故障无征兆误判现象：

1)S-A-0/1，S-D-k；

2)W-A/O。

由于等权值算法生成的测试向量具有固定的权值，通过上述的抗误判定理和推论可以得出该算法不存在征兆误判。等权值算法和改良计数算法具有相同的紧凑性指标，并且具备较强的故障检测能力[3]。等权值算法减少了征兆误判的出现，但是征兆混淆率还是较高，并且征兆混淆主要发生在相似的STV之间[5]。以表1中测试矩阵为例说明，假设n3和n7短路在一起，n4和n6也短路在一起，它们的贯序测试响应向量(Sequential Response Vector，SRV)均为11011，无法判断是哪两组网络之间发生短路,即发生混淆。等权值算法同传统的改良计数算法、WOA算法在测试生成的过程中均未能充分利用电路板的结构信息[3]，即该算法的前提仍然是假设电路板中的所有网络均可能发生短路故障。

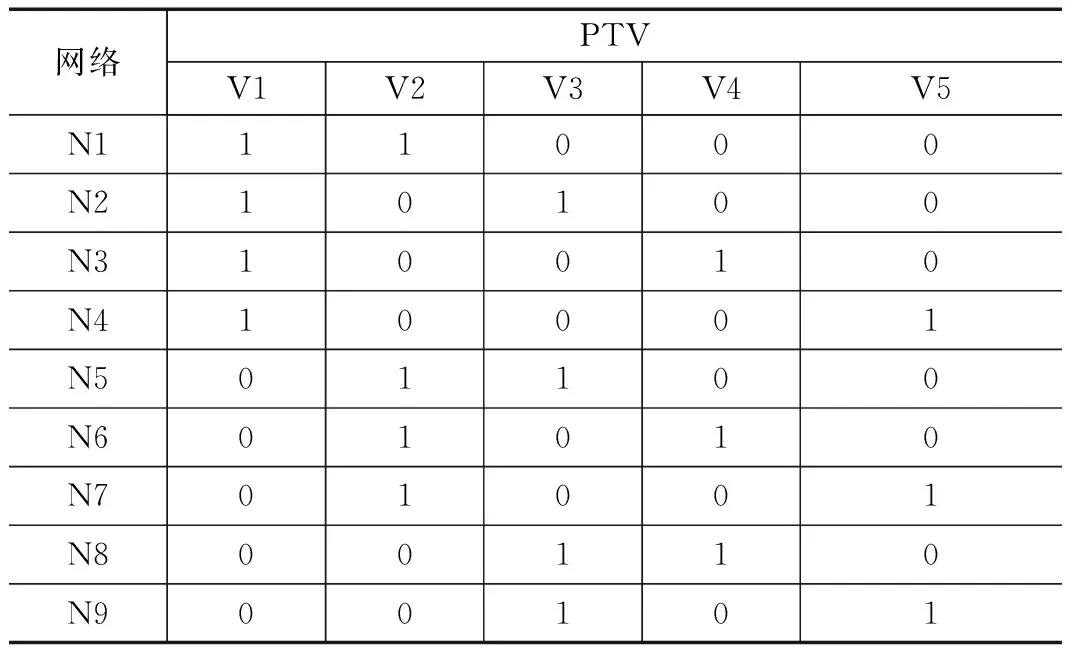
表1 等权值算法测试矩阵

2 算法改进思路及过程

2.1 算法改进思路

产生误判和混淆需要同时满足两个条件:1)算法生成的测试向量本身存在发生征兆误判和征兆混淆的可能；2)分配到发生短路网络上的STV能够满足征兆误判和征兆混淆的发生条件[8]。因此，有两种避免发生误判和混淆的方法:第1种，提高算法生成的测试向量自身抗误判和抗混淆的能力；第2种，在算法生成测试向量不变的条件下, 为网络分配STV，使误判和混淆发生条件不满足，从而降低误判和混淆的发生概率。以表1说明，如果把n2和n3的STV互换，则n3和n7短路的SRV为11101，n4和n6短路的SRV为11011，则不发生混淆。因此，若是能够对STV进行分组，将不易发生混淆的STV分在一组。同时利用电路板的结构信息对电路板网络进行适当分组，将发生短路概率大的网络分在一组。最后将把不易发生混淆的STV组分配发生短路概率大的网络组，从概率的角度上则可以降低误判和混淆发生的可能性。

目前边界扫描测试算法优化包括两类典型的问题，第一类是满足完备性指标寻找紧凑性指标最小的测试向量集，第二类是确定紧凑性指标寻找完备性指标最佳的测试向量集[6]。因此目前的算法优化方向主要集中在如何在紧凑性和完备性指标之间折中，寻求征兆误判和征兆混淆率低的测试向量集，而利用电路板结构信息优化测试向量的方法较少。

综合以上内容，陶瓷与酒的结合在历史上由来已久，对于现代酒类包装设计工作的展开来说，设计人员必须能在确保陶瓷这一传统文化元素发挥出自身作用的同时，保证酒类产品外包装设计的创新性。

2.2 算法改进过程

如前面章节中所述，分组的目标是将不发生混淆的STV分在一组，同时将易发生短路故障的网络尽可能分在同一组内。因此优化分组的过程主要分为两步，即首先是对STV分组，然后对电路板网络进行分组。

2.2.1 STV分组

通过对表1的STV进行分析可以发现，由于分配给各网络的STV具有相同的权值，网络N1、N2、N3和N4的第1位相同，第2至5位是移位“1”序列。同样N5、N6和N7的前两位相同，第3至5位是移位“1”序列，因此我们可以定义测试相似组对STV进行分组。

定义1(测试相似组[9])测试相似组是指组内的测试向量前i位值相同，i+1位至最后位由移位“1”算法组成。

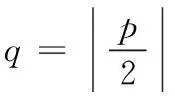
根据定义可将表1 的测试矢量集分为三个测试相似组，如表2所示。由于每个测试相似组中，相异部分由移位“1”序列组成，所以相似组内不会产生征兆混淆，不同的测试相似组之间才会产生征兆混淆。

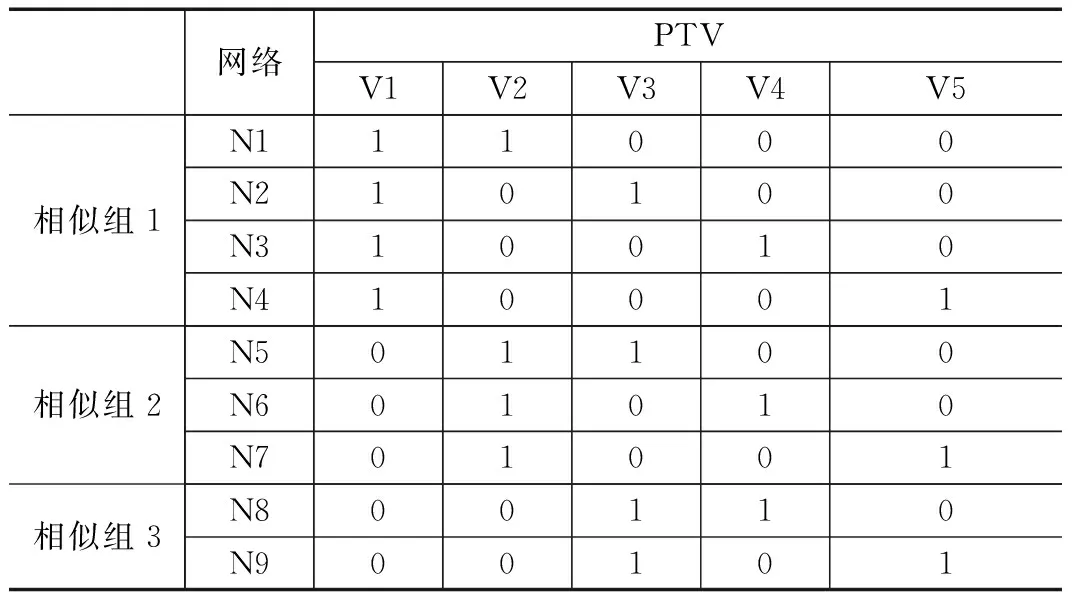
表2 测试相似组

2.2.2 电路板网络分组

研究表明,电路板的管脚之间距离的长短会对管脚之间发生短路的概率产生影响。这种影响关系可以采用衰减函数来描述,如公式(1)[7]：

(1)

其中：pm和pn代表两个任意的管脚，L0代表两个管脚间的最小距离(取决于制造工艺)，Lm代表管脚间发生短路的最大可能物理距离，L为任意两管脚间的实际距离，T0为最邻近的两个管脚间发生短路的可能性，A为远大于1的衰减系数，代表相对于管脚距离的增大短路的概率衰减大小。通过衰减函数可以看出来，不同的网络之间短路的概率不同，因此电路板网络之间的短路故障是有限制。

网络由相互连接的多个焊点构成，网络之间发生短路的可能性为各焊点短路的可能性的概率和，网络之间发生短路故障的可能性为：

(2)

将式子展开，并忽略无穷小项，可得网络之间的短路概率eij：

(3)

网络之间发生短路的可能性可以通过上式进行计算，给定阈值∂T0(不同的电路板阈值∂T0的选取不同)。当eij<∂T0时,可认为网络之间会发生短路。当eij≥∂T0时,认为网络之间不会发生短路。

通过上述计算方法，获取各网络之间的短路概率,在此基础上，建立网络短路关系图G=(V,E)，其中V={v1,v2,…,vn}，E=eij。其中vi表示网络，E=eij表示vi与vj之间短路概率，图1是某电路板的网络短路关系图[7]，下章节中将用此短路故障图为研究对象进行网络分组。图中Ni代表网络，图中网络间的权值代表短路概率，β是与电路板制造工艺有关的常数，图中权值为0的网络之间的边进行了省略。

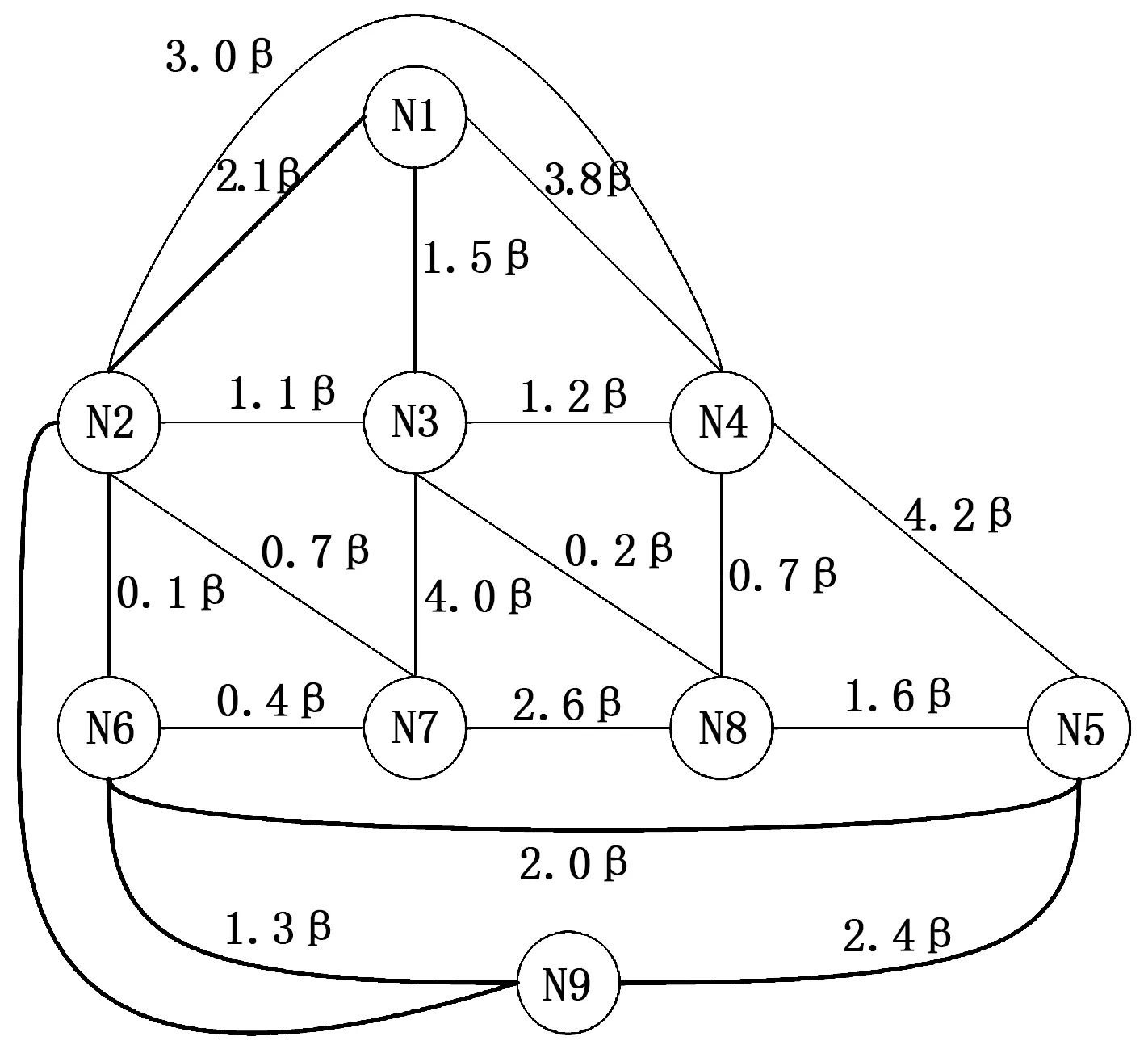
图1 某电路板的有限制网络短路关系图

2)网络分组

通过对图1的电路板的网络短路关系图的分析，可以将其等价为一个具有n个节点的无向完全图G(V,E)，其中V={v1,v2,…vn}代表网络，E=eij代表权值，即网络间短路概率。对于该无向完全图G，边集E的权值之和是个常数，因此将网络分组问题转换为无向完全图G的分割问题。即为求满足不同子图间的边权值之和最大值的分割，即满足公式(4)：

(4)

该问题是带权无向图的k-最大割问题，是NP-hard问题，目前没有多项式时间内的精确求解算法[11]。对于具有大规模网络的电路板来说，需要采用一种能够在较短的时间内获得较好的网络分组策略的方法。因此本文采用启发式分组算法。

算法的思想是，首先计算各网络之间的权值矩阵D，然后计算单个网络与其他所有网络的权值之和，根据权值之和对网络进行降序排序，选择权值之和最少的分组构造初始分组，最后再对分组结果进行优化。

对于给定的分组数k，启发式算法的主要步骤如下：

a)计算网络之间的权值矩阵D。

b)对于每一个网络vi，计算其与其它所有网络的权值之和ei=∑eij，并根据ei对网络进行降序排序。依据排序结果顺次对网络进行分组。

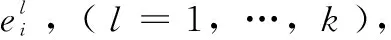
d)对分组进行优化。检查是否存在网络vi，将其从当前分组移动到另一分组时，总的权值会下降。如果存在则对vi行移动，直到找不到在这样的网络。

通过章节2.2中的电路板网络分组算法对图1所示的电路板网络短路关系图进行分组，最终分组结果为G1={n4,n1,n8,n6}，G2={n5,n7,n9}，G3={n2,n3}。

2.2.3 STV补偿

网络分组结果与章节2.2.1的STV分组结果结合，得到优化后的测试矩阵如表3所示。

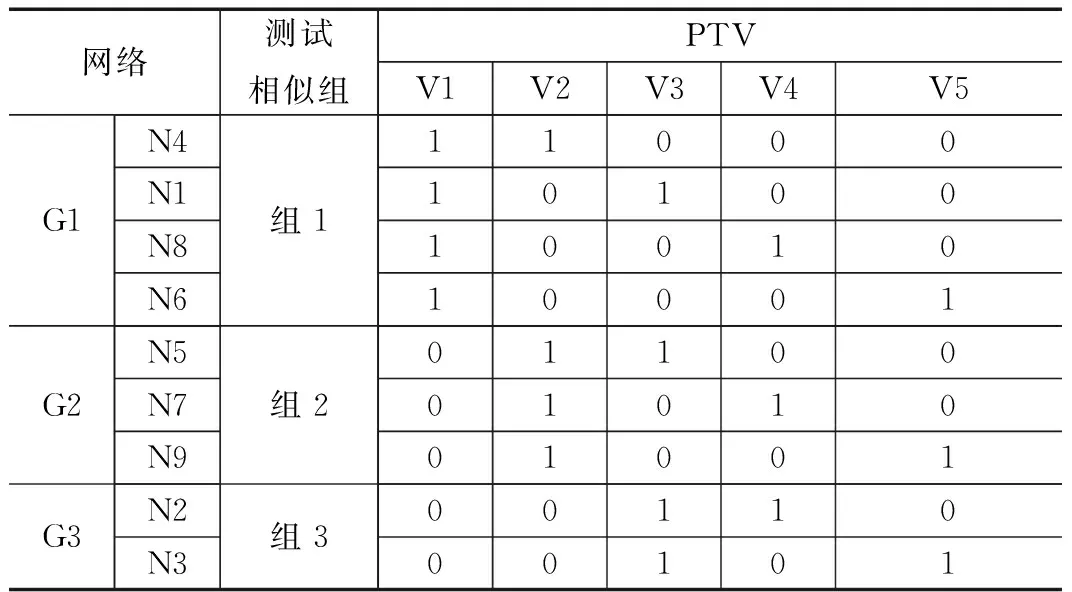
表3 优化后的测试矩阵

考虑到网络分组只是将短路概率大的网络分在同一组，而不同的网络组之间仍存在短路的可能，为了减少组间可能出现混淆，可以通过增大测试向量集的紧凑指标，从而达到完备性指标提高。由于走步“1”算法是完备性算法，可以选择走步“1”序列作为补充向量，为了满足向量的紧凑性指标要求，补充向量的个数应尽可能少，因此可以选择组间走步“1”序列，补充向量的个数与测试相似组的个数相同。表4为最终改进后的等权值测试向量集。

3 改进的算法分析

改进的等权值算法的测试向量集如上表所示，改进的算法的紧凑性指标为(P+N)，其中N为测试相似组的数目。与等权值算法相比，紧凑性指标提高了，表5给出了不同网络下数目下，两种算法的紧凑性指标。

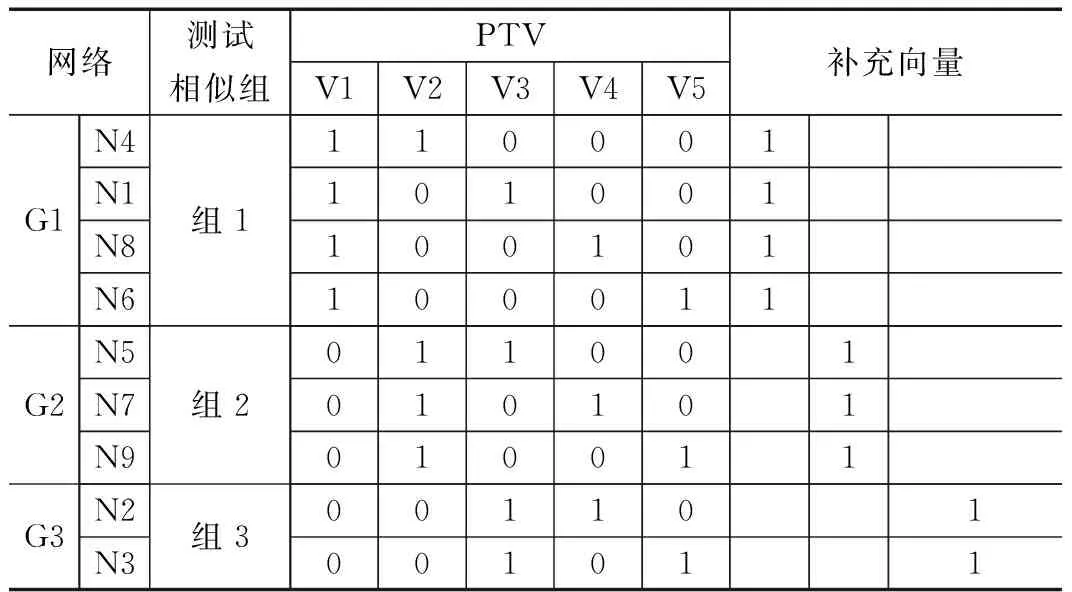
表4 最终改进后的测试矩阵

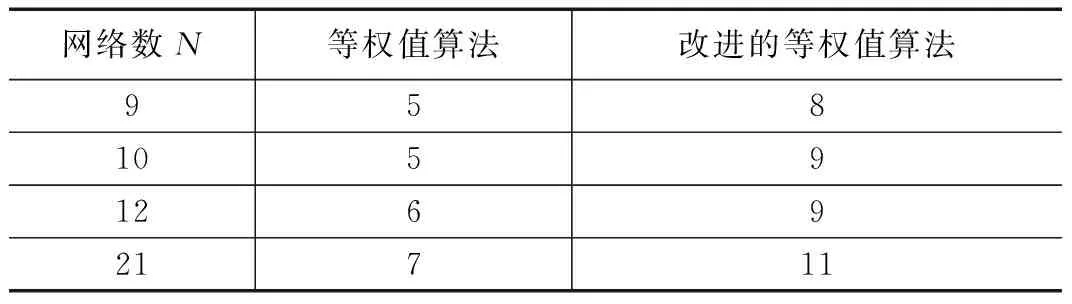
表5 两种算法的紧凑性指标比较

表6给出了不同网络下不考虑网络分组情况下的两种算法的征兆误判率和征兆混淆率。但是由于网络的合理分组，给测试相似组分配了短路概率大的网络组，因此征兆混淆发生的概率降低，改进的等权值算法的实际征兆混淆率应比表6中的数据远低。

表6 两种算法的征兆误判率和征兆混淆率

4 结论

针对等权值算法在利用电路板结构信息方面的不足,提出了一种基于网络有限制短路故障关系的改进等权值算法。与等权值算法相比,本文提出的算法充分利用了电路板结构信息，通过对测试矢量和电路板网络进行分组，给短路故障发生概率高的网络组分配不发生混淆的测试向量组，虽然不能完全避免混淆的发生，但是可以从概率的角度降低征兆混淆发生几率，从而提高等权值算法的测试能力。