动态惩罚分解策略下的高维目标进化算法
2018-10-18王丽萍张梦紫章鸣雷
王丽萍, 张梦紫, 吴 峰, 章鸣雷,叶 枫
1(浙江工业大学 信息智能与决策优化研究所, 杭州 310023)
2(浙江工业大学 经贸管理学院, 杭州 310023)
1 引 言
高维目标优化问题一直是研究的热点与难点之一.一方面,在多目标优化问题中,随着维度的增加,目标空间中的Pareto前沿性状愈加复杂,种群规模不足,使得解集难以分布整个前沿[1].另一方面,维数增大存在收敛性不足的问题,算法在平衡多样性与收敛性方面面临更严峻的挑战[2].
多目标进化算法主要分为三类[3]:
1) 基于支配的多目标进化算法,如Deb提出的NSGA-II[4]和Zitzler提出的SPEA2[5],这类算法在二维和三维问题上效果很好,但高维问题中几乎所有解都是非支配关系,搜索能力随着目标个数增加表现出明显衰减,甚至停滞[6];
2) 基于指标的多目标进化算法,如SIBEA[7]等,此类算法如超体积指标的计算成本会随着目标维度增加而呈指数型增长[8];
3) 基于分解的多目标进化算法,该类算法将多目标问题分解为多个单目标子问题,并同时优化所有子问题,有效降低计算成本,并可拓展至高维,典型算法有Zhang等人提出的MOEA/D[9]和Cheng等人提出的RVEA[10].
MOEA/D通过聚合函数将多目标问题分解成一系列单目标子问题,聚合函数与权重向量有关,由于权重向量的设置影响解在前沿的分布[11],从而聚合函数也会影响解的质量[12].
聚合函数主要有三种[13]:加权和聚合法(WS),切比雪夫聚合法(Tch)以及基于惩罚的边界交叉聚合法(PBI).WS搜索能力比Tch强[14],但WS不适用于凹形前沿问题[7],Tch虽然可以同时适用于凹形前沿与凸形前沿,但是在前沿形状较为复杂的问题中效果极差[15],而PBI在超过2维的优化问题中优于WS和Tch.
但是PBI聚合法存在一个重要缺陷,该方法对于算法收敛性与多样性的平衡由惩罚参数θ控制,而θ值是人为预设值,θ越小越倾向于提高算法收敛性,θ越大则越倾向于提高解的多样性[13],且θ越小在非凸前沿上效果越差[16].Sato等人曾提出一种反向PBI(Inverted PBI)策略[17],由于缺失边界点等原因,参考点可能会偏离真实理想解较远,种群难以逼近真实前沿,反向PBI策略通过寻找距离目标空间中最差解的收敛方向最远且分布方向最近的点来解决这个问题,然而该策略并未考虑惩罚参数θ值自身对于算法性能的影响.许多使用PBI策略的算法中都将惩罚参数值设置为原始MOEA/D算法中的θ=5.0[18],然而Ishibuchi提出在多目标knapsack问题中,θ=1.0比θ=5.0的效果更好[16],设置单一惩罚参数值解决多目标优化问题并不合理[19].因此, Yang等人提出一种自适应PBI(Adaptive PBI)策略[20],对传统PBI聚合法中的θ值进行自适应变化,使其随着算法迭代代数的增加而从小增大;设置θ值的变化范围为[1,10],目的是将θ=5.0包含在内.
但是,上述对传统PBI策略所做的研究与改进并没有对θ值的影响考虑全面,惩罚参数在整个算法进化过程中应同时考虑两方面,一方面是θ值对不同位置子问题的影响,另一方面为如何使θ值更合理地平衡算法收敛性与多样性.对此,本文提出一种基于动态惩罚分解策略的高维目标进化算法MOEA/D-DPS,使得惩罚参数θ在每个子问题上随算法迭代而各自变化.首先,根据每个权重向量分量的极值差来确定不同子问题上所绑定的θ值,然后在算法进化方向上,引入参数k来引导聚合函数进行自适应选择,从而使每个子问题上的θ值都有各自合适且不同的变化范围,动态调整不同子问题的搜索能力,保证算法在搜索早期加快收敛速度,后期尽可能维持解的多样性.
本文主要工作如下:简述了MOEA/D算法和PBI聚合方法,重点分析了PBI方法的缺陷并提出改进策略,将改进策略DPS与原始PBI策略,以及同样对惩罚参数θ进行改进的SPS策略[21]和APBI策略融入到原始MOEA/D算法中,通过仿真实验进行对比分析.实验结果表明:MOEA/D-DPS算法与其他算法相比,在大部分测试函数上所得解集整体质量更优.
2 相关背景
2.1 MOEA/D算法
Zhang等人[9]提出的基于分解的多目标进化算法(MOEA/D)基于如下m维最小化多目标优化问题:
MinimizeF(x)={f1(x),f2(x),…,fm(x)}T
Subject tox∈Ω
(1)
其中x是决策变量,Ω是决策空间,F:Ω→Rm为m维目标向量,Rm表示目标空间,fi(x)是第i个待优化的目标函数,F(x)为所得目标解集.
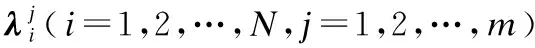
MOEA/D算法描述如下:
输入:
1) 多目标优化问题;
2) 算法停止条件;
3)N:MOEA/D中包含的子问题个数;
4)λ1,…,λN:均匀分布的N条权重向量;
5)T:每条权重向量邻域中包含的权重数量;
输出:PF:{F(x1),F(x2),…,F(xN)}.
Step1.初始化
Step1.1.计算任意两条权重向量的欧氏距离,并为每条权重向量选出T条距离最近的权重向量.对每个i=1,2,…,N,设置邻域B(i)={xi1,xi2,…,xiT)},其中λi1,λi2,…,λiT是λi的T条最小距离权重.
Step1.2.随机生成初始种群x1,x2,…,xN,设FVi=F(xi).
Step1.3. 初始化z=(z1,z2,…,zm)T.
Step2. 迭代更新
当i=1,2,…,N时, 执行以下步骤:
Step2.1. 繁殖:从B(i)中随机选择2个个体,使用遗传算子生成新解y.
Step2.2. 修正:采用启发式的改进策略修正y,生成y′.
Step2.3. 更新z:若zj Step2.4. 更新解:如果存在gte(y′|λj,z)≤gte(xj|λj,z),则设xj=y′,FVj=F(y′),j∈B(i). Step2.5. 更新PF:将PF中所有被F(y′)支配的向量移除,加入非支配F(y′). Step3. 停止条件:如果满足所有停止条件,则停止迭代,并输出PF.否则,返回Step 2. MOEA/D有多种聚合函数,本节主要讨论PBI聚合法,该策略适用于连续型多目标优化问题,在超过2维的问题中,尤其是权重向量数目不多的情况下,可以得到比切比雪夫聚合法更均匀的解[7]. 图1 PBI方法示意图Fig.1 PBI strategy illustration PBI聚合函数表示为[23]: mingpbi(x|l,z*)=d1+θd2 (2) (3) d2=‖F(x)-(z*-d1λ)‖ (4) 其中θ>0是人为预设惩罚参数,z*为理想参考点.如图1所示,PBI聚合方法由两个部分组成:d1表示F(x)在权重向量λi上的投影到参考点的距离,通过最小化d1使候选解在搜索过程中逼近最优Pareto前端,带动算法收敛;d2是F(x)与权重向量λi之间的垂直距离,用来调整解在目标空间中的分布.惩罚参数θ则定义了适度值中收敛性与分布性的比例. 3.1.1 基于同一子问题的影响 惩罚参数θ对算法性能的影响显著,其值过大或过小都会弱化算法性能.图2直观地表示了θ在不同取值下,目标函数等高线形状不同,其中阴影部分代表个体i的占优区域,即阴影区域内的个体无法支配个体i,空白区域内的个体可以支配个体i.从左到右依次对比三幅图可以发现,随着惩罚参数增大,个体i的占优区域扩大,即个体i成为非支配个体的概率增加(一个个体成为非支配个体的概率=阴影区域面积/(空白区域面积+阴影区域面积)),从而使个体i在迭代过程中更容易保留到下一代,有利于维持种群的多样性.反之,惩罚参数越小,可以支配个体i的个体数量越多,个体i在迭代过程中被替代的可能性增加,从而有利于促进种群迭代,加快算法收敛速度. 图2 θ=0,θ=1,θ=2时PBI等高线示意图Fig.2 Illustration of PBI contour lines with θ=0,θ=1,θ=2 3.1.2 基于不同子问题的影响 图3示意图中有7条代表不同位置的权重向量,表示7个不同的子问题,加粗实线表示惩罚参数为1的情况,加粗虚线表示惩罚参数为5的情况,以权重向量λ1和λ4为例.向量λ1位于边界处,λ2与之相邻,解A和解B分别为向量λ1和向量λ2对应子问题上的理想最优解,解B在解A邻域范围内,当惩罚参数为1时,如解A处实线所示,解B在实线与坐标轴区域范围内,即解B的目标函数值小于解A的目标函数值,所以在更新替代过程中解A点将被解B替代;当惩罚参数为5时,如解A处虚线所示,解B在虚线与坐标轴区域范围之外,表示解B的目标函数值大于解A,所以更新时解A将被保留进入下一次迭代.显然,对于边界子问题而言,惩罚参数过小容易丢失边界点,难以维持前沿形状,最终损失了解的多样性. 图3 不同子问题上的解在θ=1和θ=5时的更新示意图Fig.3 Update illusion of the solutions on different sub-problems with θ=1 and θ=5 权重向量λ4位于中间位置,解C是该向量上所绑定的解,解D是该向量邻域内的解,相对于解C和解D来说,解D距离标准前沿比解C近得多,解D若可以保留进入下一次迭代有利于算法收敛到前沿,但当惩罚参数为5时,即如解C处虚线所示,解D位于解C的目标函数等高线之外,表示解D的目标函数值比解C处大,所以更新时解D将不会被保留;当惩罚参数为1时,如解C处实线所示,解D目标函数值比解C处小,此时解D可能进入下一次迭代.所以对于中间位置的子问题来说,较大的惩罚参数值不利于带动解的收敛,若惩罚参数值过大甚至可能导致解无法收敛到Pareto前沿. 采用PBI策略时如果设置一个固定的惩罚参数,则该参数值对于临近边界的子问题来说容易偏小,从而丢失边界点,而同样的参数值对于位于中间的子问题来说也许偏大,阻碍了解的收敛.基于以上对PBI策略中惩罚参数值的缺陷分析,本文提出一种基于动态惩罚分解策略的高维目标进化算法MOEA/D-DPS.该问题可以通过改变惩罚参数的性质来解决,使惩罚参数值在算法初始化时,根据权重向量位置的不同,对每条权重向量分别绑定一个合适的值,即使惩罚参数值从中间向量向边界向量逐渐递增,由此给每个子问题都分配了一个合适的惩罚参数. 但是,若每条权重向量上所绑定的惩罚参数在算法进化过程中为固定值,那么中间向量所绑定的惩罚参数从算法迭代开始到结束始终维持在很小的值,在算法后期不利于解的均匀分布.同样,边界向量所绑定的惩罚参数若始终维持较大的值,在搜索早期将阻碍算法收敛,甚至导致边界点收敛不到前沿.该问题可以在算法迭代的过程中通过动态调整各个子问题上所绑定的惩罚参数来解决,在搜索早期采用较小的参数值,确保算法的收敛性,在算法后期采用较大的参数值,更好地平衡算法的收敛性与多样性.由此每个子问题上绑定的惩罚参数在算法进化过程中都有各自合适的变化范围. 改进后的惩罚参数公式如下所示: θi=e(kmin→kmax)wi (5) (6) λmid={λp|arg minwi} (7) λbou={λp|arg maxwi} (8) 其中,公式(5)中的θi表示第i个子问题上绑定的惩罚参数值,k表示一个由小增大的正数,用于引导θi随算法进化而动态调整,设kmin=1,kmax=10,确保动态变化过程中包含θ=5这个基本值.wi∈[0,1]是第i条权重向量的向量分量极值差,即通过计算该权重向量的向量分量最大值与最小值之差所得,所以公式(5)中的wi在算法初始阶段可以通过公式(6)计算得出,因此,惩罚参数θi的大小在算法进化过程中的变化由k值的变化决定.公式(7)中的λmid代表中间向量,即位于中间位置的权重向量,公式(8)中的λbou代表边界向量,即位于边界位置的权重向量,中间向量的wi趋于0,比如二维目标中的向量(0.51,0.49),边界向量的wi趋于1,比如向量(0.99,0.01).由此,每个子问题上都绑定了一个不同的惩罚参数,且随着算法进化都有各自不同的变化区间,不仅提高了不同位置解的质量,还平衡了不同搜索时期算法的收敛性与多样性. 正如惩罚参数公式(5)-公式(6)所示,惩罚参数值随算法进化而动态调整是由k值的变化决定.k值在算法搜索早期较小,目的是促进候选解的收敛,之后随着进化代数逐渐增大,使算法在促进收敛的同时,尽可能维持算法的多样性不下降.本文对k值做三种最典型的变化[23],通过仿真实验进行对比,选择实验结果最优的一种变化趋势带入改进的动态惩罚分解策略, 在后文中与其他算法进行仿真实验对比. 三种k值变化公式如下: (9) (10) (11) 其中kmax为k值最大值,本文中设置为10,目的是使算法迭代过程中包含θ=5. 图4k值的三种线型变化示意图 klin、kexp、ksig三个公式分别表示k值作线性变化、指数变化和S型变化.其中S型变化中的σ设为0.5,该参数取值将在后文参数分析中加以说明.图4是三种k值变化线型示意图,直观地表示了三种曲线的增长趋势. 为验证改进后的动态惩罚分解策略在算法中的性能有效性,本文选用一种测试高维目标优化问题较普遍的DTLZ1-4系列测试函数进行仿真实验,并与基于PBI策略的原始MOEA/D算法,即MOEA/D-PBI[9],以及同样对惩罚分解策略进行改进的MOEA/D-APBI[20]和MOEA/D-SPS[21]进行对比分析. 由于PBI策略适用于2维以上问题,所以本节选择在3、5、8、10维四个目标维度上进行仿真实验.其中邻域大小T=20,杂交算子pc=1.0,杂交位置为2,变异概率pm=1/n,n为决策变量个数,变异位置为5.目标维度为3维时,最大进化代数在测试函数DTLZ1-2和DTLZ4上设为500代,DTLZ3设为1000代,目标维度为5、8、10维时,最大进化代数在测试函数DTLZ1-2和DTLZ4上设为1000代,DTLZ3上为2000代,原因是在DTLZ3测试函数上,初始种群距离前沿很远,需要更大的进化代数.种群大小N在3、5、8、10维上分别为105、126、156、275,仿真实验在所有测试函数上各运行20次, 所有指标均取20次结果的均值及标准差. 实验结果用IGD[24]指标(Inverted generational distance)、HV[25]指标(Hyper Volume)、GD[26]指标(Generational Distance)和SP[27]指标(Spacing)来衡量解集质量.其中IGD指标和HV指标可以评估解的综合性能,IGD值越小,解的整体质量越高,而HV值越大,则算法综合性能越好;GD指标用来衡量算法收敛性,值越小,算法所得解集越逼近PF,表明算法收敛性越好;SP指标衡量所得解在PF上的分布均匀性,值越小,分布越均匀,算法多样性越好. 4.2.1σ参数分析 本文对k值做了三种变化,首先对S型变化中的σ进行参数分析.σ取值范围设为[0.1,1.0],仿真实验在3维DTLZ1-4四个不同性质的测试函数上进行,计算所得解集的GD值和SP值,每个σ值代入公式(11),算法独立运行20次取均值,所得结果如图5所示. (a) DTLZ1-4测试函数的SP指标对比图 (b) DTLZ1-4测试函数的GD指标对比图图5 DTLZ1-4测试函数的SP(a)和GD(b)指标对比图Fig.5 SP(a) and GD(b) values of the analysis of σ 从图5(a)的SP指标对比结果来看,σ=0.5时在DTLZ3和DTLZ4上得到最小SP值,表示此时算法多样性最优,σ=0.2、σ=0.7、σ=0.9和σ=1.0时,SP值明显大于σ其他取值时所得结果,且σ=1.0时SP指标远大于σ=0.1处,折线图总体以0.5为低峰向两边增大;在DTLZ1-2及DTLZ4上,σ值的变化对SP指标影响较小,但也能发现DTLZ4上σ=5时SP值最小,DTLZ1上σ=1.0处SP值显然呈上升趋势. 从图5(b)的GD指标对比图来看,在DTLZ3上,σ在[0.1,0.5]上的GD值呈下降趋势, 且斜率较大,σ在[0.5,1.0]上的GD值呈上升趋势,且变化幅度比[0.1,0.5]区域小,GD值以σ=0.5为最小值向两边递增;在DTLZ1-2及DTLZ4上,σ值的变化对SP指标影响不大. 综合来看,在4个测试函数上,GD值和SP值的变化在DTLZ1-2和DTLZ4上变化不大,在DTLZ3上的变化较大,其原因可能是因为DTLZ3测试函数是多峰函数,而本文所提出的动态惩罚分解策略由于考虑了不同位置的权重上应设置不同的惩罚参数,所以对多峰函数的优化效果更显著.此外,DTLZ3上的SP和GD值都呈现出两边高、中间低的变化趋势,究其原因在于公式(11)的S型变化公式中分母随算法进化代数增加而产生的变化对于σ取值有局限性.当σ=0.5时,gen>(1/2)*Maxgen代之后,k值才开始逐渐趋向最大值,即算法的搜索周期正好被一分为二,前半个周期中k值很小,从而使得惩罚参数θ值始终处于较小的变化范围,算法趋向于促进解的收敛,在后半周期中反之,k值突然增大,使得惩罚参数θ值增大,算法逐渐以维持解的多样性为主. 表1 MOEA/D中融入k值三种线型HV指标对比结果Table 1 HV value by MOEA/D using three different lines of k 然而,当σ=0.1时,在gen>50代开始,k值就逐渐开始向最大值逼近,但此时目标空间中的解集可能并未收敛到前沿,k值的快速增大为时过早,损害了算法的收敛性,导致GD指标值过大.同理,当σ=1.0时,在进化代数达到最大进化代数的时候,k→0.5×kmax,即此时的k值最大值只能取到当σ=0.5时的k值最大值的1/2,从而导致惩罚参数θ值偏小,算法始终强调收敛性,无法合理调整解在目标空间中的分布,导致SP值过大,丢失了解集的多样性.由此,本文设S型变化中的参数σ=0.5来进行后续仿真实验. 4.2.2k值变化仿真分析 表1是将使用三种不同k值变化的动态惩罚分解策略分别融入原始MOEA/D算法后,在3、5、8、10四个目标维度的DTLZ1-4系列测试函数上求得的HV指标值.实验结果表明:在3维DTLZ1、10维DTLZ2和DTLZ3、以及5维DTLZ4上,MOEA/D-Klin或MOEA/D-Kexp所得结果最优,而MOEA/D-Ksig次之;在3维DTLZ3上,线性变化MOEA/D-Klin和指数变化MOEA/D-Kexp均优于S型变化MOEA/D-Ksig;除此之外,所有结果中,S型变化MOEA/D-Ksig所得HV均值均为最大值,可见MOEA/D-Ksig算法所得解集质量为三者最优.这可能是因为当k值呈指数变化时,惩罚参数值在大部分时期都较小,仅在迭代快结束时突然增大,使得算法过于强调收敛,损失了解集多样性,导致算法性能下降;当k值呈S型变化时,惩罚参数值在算法前期始终处于较小的值,有利于算法完全收敛到前沿位置,在算法中期变化较大,使得惩罚参数在中后期的值维持在一个较大的值,充分保证了解集在目标空间中的均匀分布,所以算法所得解集整体质量更优;而当k值呈线性变化时,惩罚参数值随着进化代数增加而均匀增大,可能会产生未完全收敛到前沿的结果.因此,在k值的三种变化中,S型变化最合适,本文后续仿真对比实验将选择对k值采用S型变化. 图6 4种算法在DTLZ1-4系列测试函数上的IGD走势图Fig.6 Change of IGD value on DTLZ1-4 by four different algorithms 为了验证使用动态惩罚分解策略的算法性能,减少随机因素对算法的影响,在每个测试函数上,MOEA/D-PBI、MOEA/D-APBI、MOEA/D-SPS及MOEA/D-DPS四种算法各自独立运行20次,取HV平均值与标准差作为最终HV指标实验结果,以及绘制IGD值最小时的IGD走势图,以便直观地表示出各算法在3、5、8、10维DTLZ1-4系列测试函数上的算法性能,从而衡量解的整体质量和算法的收敛效果. 4.3.1 基于IGD指标的比较 图6是四种对比算法在DTLZ1-4系列测试函数上的IGD值随进化代数增加而变化的趋势图,且每张图都包含了1/2进化代数后的IGD趋势子图,清晰又直观地展现了各算法的IGD走势,其中三角形、星形、正方形、圆形线条分别表示MOEA/D-APBI、MOEA/D-SPS、MOEA/D-DPS和MOEA/D-PBI四种算法. 首先纵向分析图6子图,对比同一测试函数、不同目标维度上的IGD值,可以发现随着目标维度的增大,算法最终所得IGD值逐渐增大,这说明算法性能随着维度的增加会逐渐衰减,其原因在于随着目标维度的增加,Pareto前沿性状越来越复杂,算法收敛到Pareto前端需要更多的进化代数,而改进后由动态惩罚分解策略引导的MOEA/D-DPS算法随着目标维度增加所得最终IGD值仍然严格优于其他三种对比算法,说明改进后的算法随着目标增加所得解集的整体质量仍然比其他三种算法更高. 综合来看,1、在3维DTLZ3、8维DTLZ1上MOEA/D-DPS算法所得IGD值在算法前期较大,而在算法后期逐渐减小至小于其他三种算法,这可能是因为这两个测试函数均为多峰性状,而DPS策略中每个子问题初始的惩罚参数由权重向量的位置决定,且随算法进化而动态调整,尤其位于峰谷附近的子问题所关联的惩罚参数值相差更大,所以多峰函数易使惩罚参数的分布更加不规则, 从而增加算法前期的不稳定性;2、在10维DTLZ2和DTLZ4上MOEA/D-DPS算法所得IGD值在算法前期同样较大,而在算法后期优于其他三种算法,这可能是因为目标维度较大,增大了DPS策略在算法运行过程中的不稳定性;3、除此之外,MOEA/D-DPS算法在其他所有测试函数上的IGD值均严格优于其他三种算法,且随着算法进化代数的增加,IGD值的趋势平稳.这说明MOEA/D-DPS算法性能更优. 4.3.2 基于HV指标的对比 表2是四种算法在3、5、8、10维DTLZ1-4系列测试函数上的HV指标仿真实验结果,其中加粗部分是同一测试函数上所得HV最大值,表示其对应算法所得解集的整体质量优于其他三种算法.分析表3结果可以得到:1、在3维DTLZ2和8维DTLZ4上,MOEA/D-SPS和MOEA/D-PBI算法所得HV指标均值最大,MOEA/D-DPS次之;2、在3维DTLZ3和5维DTLZ4上,MOEA/D-DPS算法所得结果弱优于其他三种算法的HV值;3、在其他所有测试函数上,MOEA/D-DPS算法所得HV均值均严格优于其他三种算法;4、MOEA/D-APBI 算值均严格优于其他三种算法;4、MOEA/D-APBI 算法在所有测试函数上的HV指标都为最小值,算法性能最差,这是因为在PBI策略中仅仅使惩罚参数随着进化代数呈现自适应变化是远远不够的,尤其是在高维目标问题中,没有对测试函数形状、权重向量位置等因素加以考虑,无法有效平衡算法的收敛性与多样性,而MOEA/D-DPS算法在为不同位置的子问题分配合适的惩罚参数的基础上,使其根据算法的进化而动态调整,从而使所得解集的整体质量比MOEA/D-APBI算法更高, 且大部分结果亦优于MOEA/D-PBI算法和MOEA/D-SPS算法. 表2 MOEA/D-DPS算法与MOEA/D-PBI、MOEA/D-SPS、MOEA/D-APBI的HV指标对比结果Table 2 HV value of MOEA/D-DPS、MOEA/D-PBI、MOEA/D-SPS and MOEA/D-APBI 本节给出了四种算法在DTLZ4测试函数上的仿真前沿图,图7是各算法独立运行20次之后所得IGD值最小的一组前沿对比.在3维前沿图中,"+"代表标准前沿,实心圆点代表算法所得真实前沿.在5、8、10维前沿图中,所示线条即为算法所求解集. 图7 各算法在DTLZ4测试函数上的前沿对比Fig.7 Pareto fronts of four different algorithms on DTLZ4 由图7可知,在3维真实前沿上,MOEA/D-PBI和MOEA/D-APBI的解集集中分布在各顶点附近,中间位置难以收敛,MOEA/D-SPS可以收敛到距离中心较近的区域,而由动态惩罚分解策略所引导的MOEA/D-DPS算法则收敛到了中心区域,可见其多样性相比其他算法更好.在5维上,MOEA/D-PBI的前沿线条浓度最浓,表示位于同一位置的解较多,提供其他位置信息的能力相比其他三种算法而言不足;而MOEA/D-DPS的前沿线条浓度较淡,原因在于其所得位置信息最多,解的分布范围广,多样性优,比如在[0.8,1.0]区域获得了4个位置信息,而其他三种算法只能够得到3个位置信息.目标维度为8时,在[0.15,1]区域中,MOEA/D-SPS和MOEA/D-DPS的均匀性更好,MOEA/D-PBI和MOEA/D-APBI的线条较杂乱,而在[0,0.15]区域中,MOEA/D-DPS的解集较为清晰地分出了两个层级位置,MOEA/D-PBI只分出了一层,而MOEA/D-SPS和MOEA/D-APBI在这一区域中解集十分混乱,无法分出层级,这说明MOEA/D-DPS算法在8维目标维度上所得多样性更优.在10维上,四种算法在[0,0.15]区域中的线条都较杂乱,但相比之下,MOEA/D-DPS与MOEA/D-PBI两种算法所得线条清晰度更好,且MOEA/D-DPS所得线条浓度比MOEA/D-PBI淡,说明所得解集位置信息更多,即此时解集多样性优于MOEA/D-PBI.因此,改进后所得MOEA/D-DPS算法性能优于其他三种算法. 为了优化PBI策略,更好地平衡算法收敛性与多样性的冲突,提高高维目标优化问题中解集的整体质量,本文提出一种基于动态惩罚分解策略的高维目标进化算法MOEA/D-DPS.该算法通过计算每条权重向量的向量分量极值差,为每个单目标子问题绑定合适的初始惩罚参数,并且随着算法进化对该参数进行动态调整,从而提高边界点的多样性与中间点的收敛性,同时使算法在搜索早期促进收敛, 后期以维持多样性为主,由此提高解集的整体质量. 仿真实验证明:MOEA/D-DPS算法所得解集质量更优,改进后的动态惩罚分解策略对算法性能的提高是有效的.在未来的工作中,我们将继续研究优化高维目标问题和具有复杂Pareto前沿的多目标优化问题,并应用到实际问题中.2.2 聚合方法


3 改进策略
3.1 PBI聚合缺陷分析
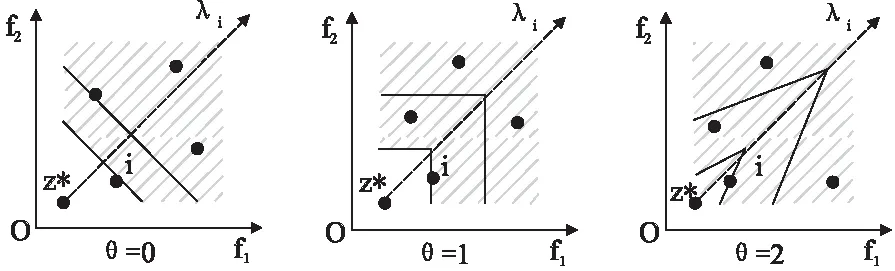
3.2 动态惩罚分解策略

3.3 k值变化


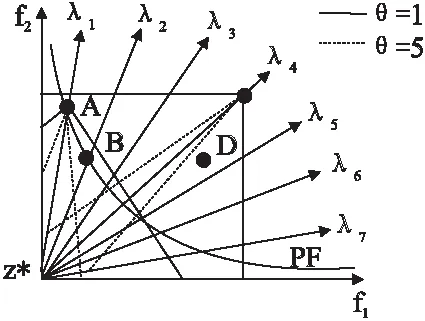
Fig.4 Three different lines or curves ofk4 实验结果与分析
4.1 实验设置
4.2 k值三种变化仿真结果
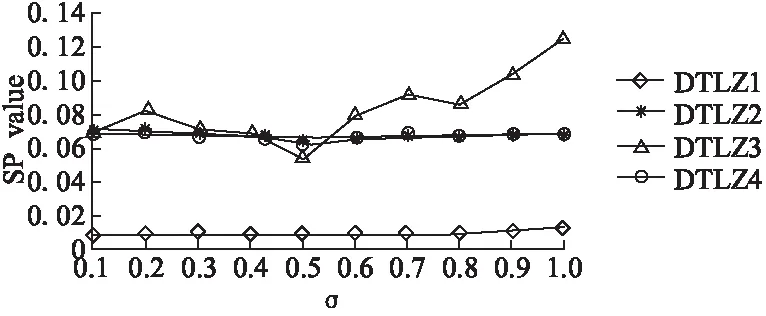

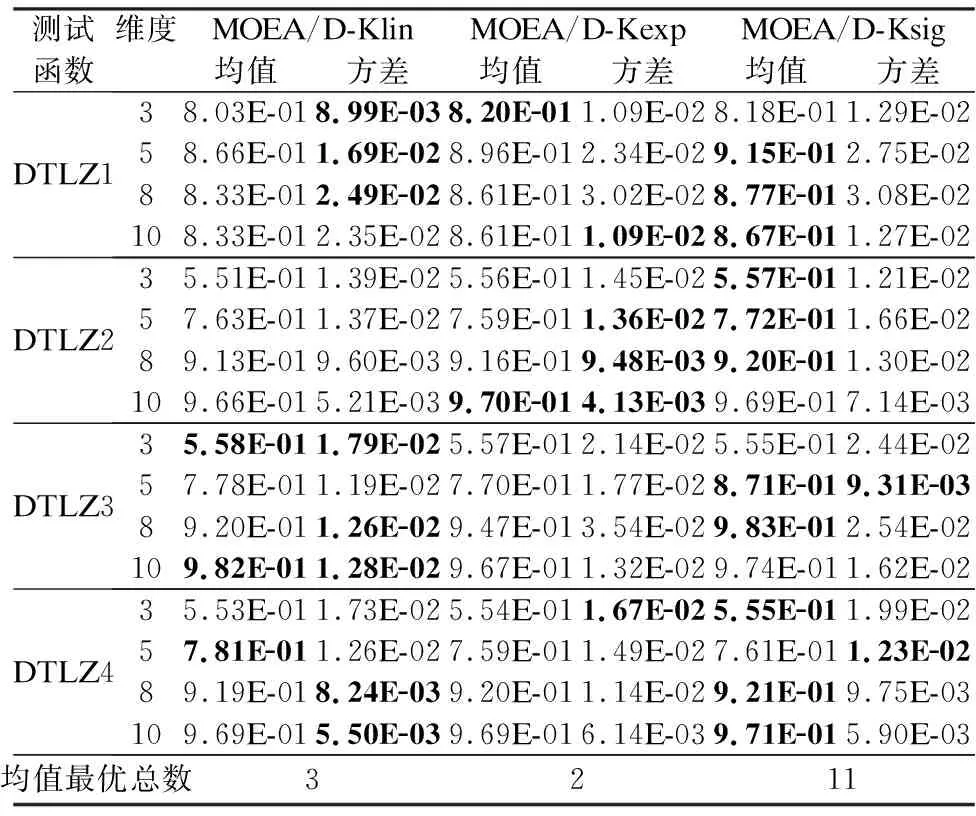

4.3 各算法的指标对比分析

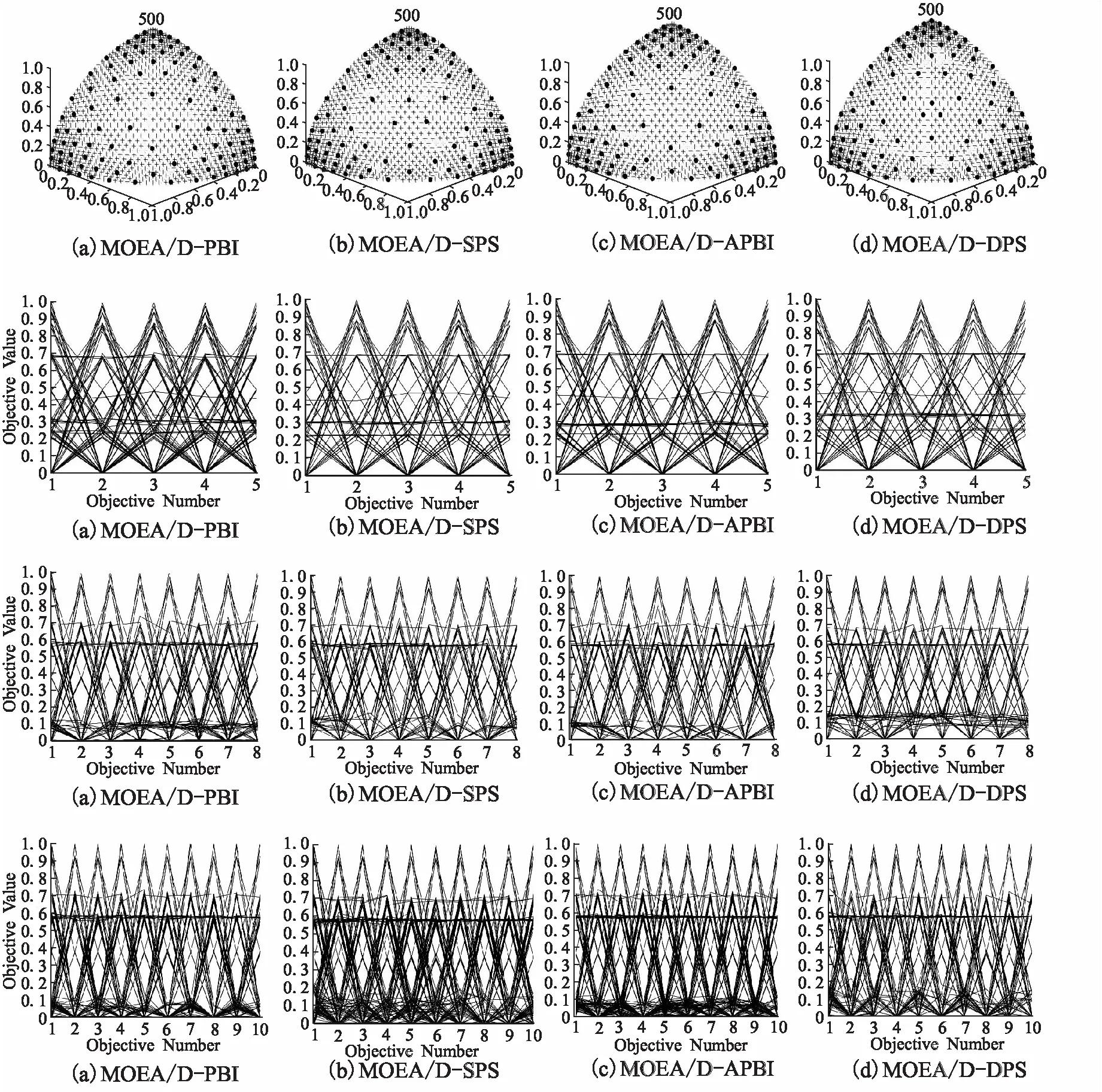
4.4 各算法的前沿对比分析
5 结论与展望
