构造法解高考数学题例析
2018-10-18秦绪君濮安山扬州大学数学科学学院江苏扬州225002
秦绪君 濮安山 扬州大学数学科学学院 江苏扬州 225002
1.构造函数
构造函数法,即根据问题中的数量关系,构造一个或几个新的函数,把原问题转化为研究函数的性质,并利用单调性、奇偶性等函数性质来解决原问题,利用构造函数来沟通问题的题设与结论的联系,使隐含关系在构造中展现出来,从而使较复杂 问题变得简单易解。

分析:本题考查等比数列的通项公式与前n 项的积的最大值。正向思维直接入手解决前n 项积最值要转化为配方法求解二次函数最值问题,解法较麻烦且易出错,而通过数列{?}通项公式与函数单调性相结合,可直接求解前n 项积?最大值,能更快速解决此类题。

2.构造方程
构造方程法,即根据题目的已知条件和结论、性质与特征,构造出某 种方程模型,然后根据方程的理论使问题在新的关系结构下得得以解决,构造方程解题基于对问题的整体性 认识和把握,关键是要挖掘出构造方程的隐含条件,利用该方法行高中数学的解题,可以增强高中生的观察能力,发展学生的数学思维。

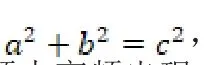
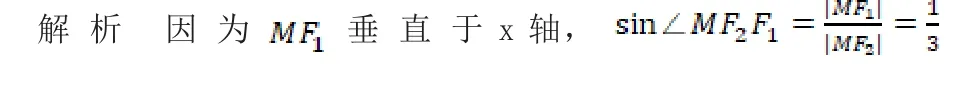
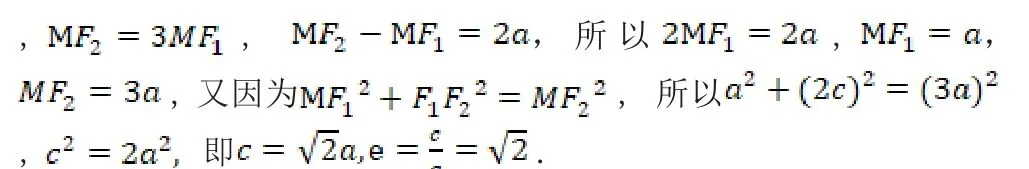
3.构造图形
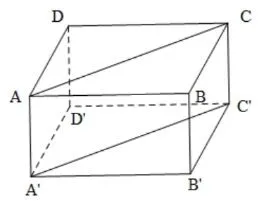
构造图形法是通过观察代数问题的条件或结论中的数量关系中的几何意义或试图以某种形式与几何图形建立联系,将题设条件与结论在图形中得到实现,通过数形结合寻求原问题的结论的方法,体现了数与形转化思想,充分的利用了几何的直观性,且解法简单,并能够培养学生解题的创造性思维。

分析: 本题考查异面直线所成角问题.求解该类问题时我们通常用到几何法和向量法。向量法即通过建立空间直角坐标系后构造直线的向量,利用空间向量的夹角公式求其夹角,从而计算两直线成角余弦值正弦值,我们发现该题目题若运用几何法,对直三棱柱进行填补,构造出四棱柱,利用图形求出异面直线成角,省去了建立坐标系的繁琐,为学生解题节约时间,提高效率。

4 构造数列
构造数列法是指在解决相关数列问题时,可根据题设中的特征,通过联想、替换构造出一个新的等差数列或等比数列,并利用该等差数列或等比数列的性质来解决问题,有关等差数列、等比数列的性质,不仅是教材中的学习的重点, 也是各类考试考点之一,比如通过构造等差数列或等比数列来求数列的通项公式,是求通项公式的重要方法也是高考重点考查的数学思想。
通过以上分析可以发现,构造法是一种灵活性很强的数学解题方法,在数学高考中有着广泛的应用。构造法在数学解题中的运用,能够使学生积极开动脑筋,主动思考,学会分析问题与解决问题,对同一问题进行不同形式的构造与分析,并不断地思考与交流,不仅能够帮助学生开拓解题思路节省了解题时间,同时在一定程度上也培养了学生的创新能力和多元化思维,对高中数学教学质量的提高起着至关重要的推动作用,值得在数学解题中积极倡导与应用.
