三角函数最值问题浅谈

范登林 西昌市第七中学

研究三角函数的最值问题，其方法与求三角函数值域的方法类似。先通过三角恒等变换，使目标函数变量归一，函数名称归一，然后利用基本函数的值域，求得原函数的最大值与最小值。在实际操作过程中，要注意换元法的应用并注意函数定义域的限制。

求解三角函数最值问题的基本思想：

1、认真观察函数式，分析其结构特征，确定类型。

2、根据类型，适当地进行三角恒等变形或转化，这是关键的步骤，具体可考虑：①将函数式化成y= Asin(ω x+φ)或y = A s in(ω x + φ ) = f(x)形式，再利用正弦函数的有界性求出最值；②通过换元，将函数解析式化成二次函数、二次方程进行求解，需要注意的是，在换元后，要注意新变元的取值范围；③转化为可利用不等式性质，均值不等式来求解的问题；④转化y为可利用函数的单调性来求解的问题；⑤改变主元，视函数为辅元，从而通过判别式法来分析的最值问题；⑥化归为可利用几何解释来解决的问题。

3、通常可考虑降次，积化和差与和差化积、引入辅助角、万能代换、换元、配方而对函数式进行变形或转化。

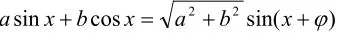
1、利用辅助角公式

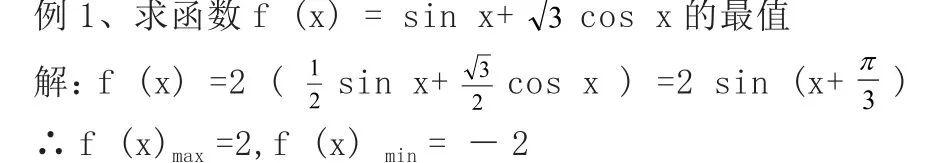
二、利用给定取间二次函数的性质——形如y=at+bt+c二次函数的最值

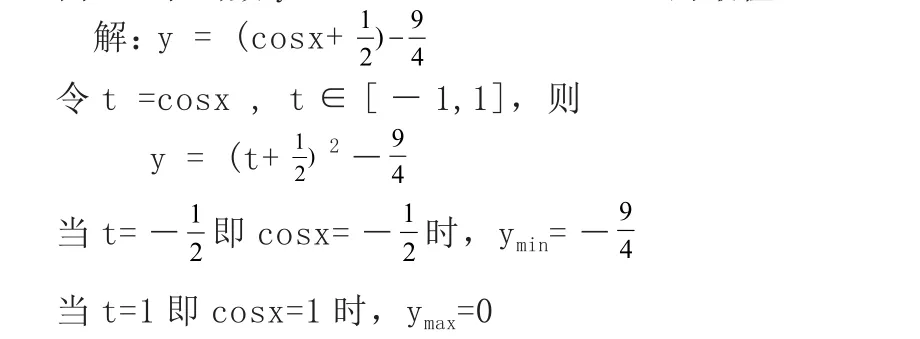
*关键：换元、配方，注意新变量的取值范围例2、求函数y = cosx +cos x－2的最值

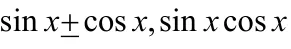
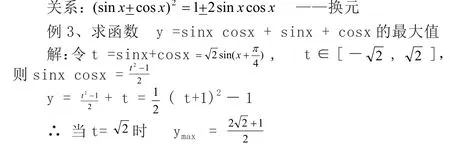
四、利用三角函数的有界性

说明：有些题目可能用以上方法无法解决，或者是可以解决但是很复杂，这时可以考虑运用导数来求解。最好与求导数极值的知识相联系起来。只不过这里是关于三角函数而已。

注：以上所列举的方法仅是从一般求解方法上来说的，可能并不适用于所有题目。有些题目比较特殊，无法用以上方法来解，而有些题目用以上很多方法都能解决，这时我们要具体情况具体分析，就要注意选择简单恰当的方法来解决。