考虑用电行为偏好的空调负荷代理商市场报价策略研究

章三华，胡 业

（1.国网江苏省电力有限公司 响水县供电分公司，江苏 盐城 224600；2.国网（江苏）电力需求侧管理指导中心有限公司，南京 210019）

随着经济的发展，空调负荷在夏季和冬季高峰时刻占比越来越高。空调工作时，由于室内温度变化的迟滞，短时间的关闭使用或者减少功率对用户舒适度影响不大。

设立空调负荷代理商作为分散的空调负荷与系统之间的中间商，一方面可管理一定区域中分散的、数目庞大的空调负荷；另一方面可以把众多空调负荷整合起来，作为一个整体参与市场竞价。文献［1］研究了空调负荷聚合商与电力公司的双层优化调度和控制模型，在考虑用户舒适度基础上，通过直接负荷控制对空调负荷进行控制以达到削减负荷的目的，但是没有涉及到用户报价问题，缺少用户与系统的信息沟通。针对负荷代理商报价策略，文献［2］考虑代理商在电力市场的灵活报价和不灵活报价，通过动态规划理论来决策代理商在能量市场和备用市场报价策略问题。文献［3］介绍了代理商管理电动汽车参与日前和实时调整市场的竞价结构。然而，在上述研究中，通常假设负荷代理商是电力市场价格的被动接受者，忽略了代理商在市场报价对市场出清电价的影响。

基于上述考虑，本文在开放的电力市场环境下，提出了考虑用户行为偏好的空调负荷代理商报价策略双层优化模型。

1 空调负荷代理商市场交易过程

市场结构如图1所示，每个代理商管理一定数量的空调，在用电紧张时（本文只考虑夏季）参与电力市场交易和系统调度，代理商根据用户效益最大的原则选择合适的报价策略，系统根据社会效益最大的原则出清空调负荷电价（下文中的电价均为空调用电电价）。最后在考虑用户舒适度的情况下对用户空调进行控制。

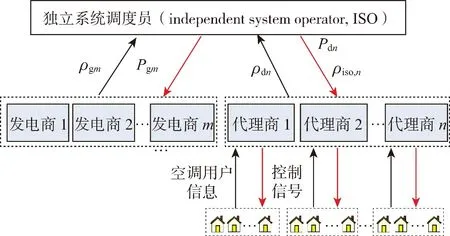
图1 空调负荷参与市场交易结构

ISO是批发市场的清算主体。市场的出清模式参考美国PJM市场。发电商和空调负荷代理商都向批发市场提交次日各时刻的报价，ISO根据市场中竞标者提交的报价情况，决定竞标者次日该时刻在市场中的电量分配。空调负荷代理商在接收空调用户用电行为信息的基础上，通过历史数据预测其他发电商的报价来确定自身的报价策略，在批发市场参与日前能量市场竞价。

整个交易过程步骤如下：

（1）空调用户根据空调型号、自身用电行为、次日用电需求等信息向所属代理商进行申报。

（2）空调负荷代理商对空调用户所申报的信息进行汇总，并根据用户所申报的信息向电力交易中心提交用电需求函数或者报价，以用电效益最大为目标制定最优的报价策略。

（3）电力交易中心接受所有空调负荷代理商的报价（或者需求函数）以及发电商、其他可控负荷代理商的报价，基于社会效益最大化和电力供需平衡进行市场清算，得到统一的结算电价和空调负荷代理商的用电量。

（4）空调负荷代理商成功购入电量，进行用电量分配和对整个系统交互中断的控制。

（5）空调负荷代理商依据统一结算电价得到总成本，按照预先设定的规则对空调负荷用户进行成本或收益分配。

2 空调负荷电力需求模型

2.1 空调可控负荷容量模型

空调机组可以用简化的等效热参数模型［4］来表示其热动力学原理，在此基础上进行化简，可以建立空调功率与室温的关系

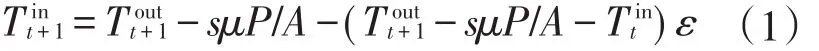
式中：P为空调机组的制冷功率；Tout、Tin分别为室外和室内气温；s为空调状态，1表示空调开启，0表示空调关闭；ε为散热系数；μ为空调能效比；A为导热系数。考虑到人体的舒适度，设定允许温度的最大和最小值

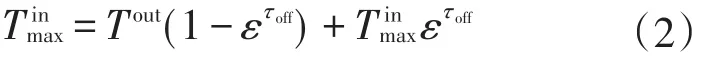
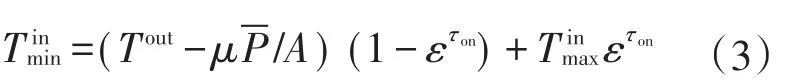
式中：τon、τoff分别为空调开启和关停时间，周期为τc，τc=τoff+τon。大量空调的可控部分参与系统调度时，空调可控负荷容量Cx计算如下

2.2 考虑用户偏好的空调负荷需求模型

用户可根据电价的波动情况，在满足舒适度的前提下决定空调用电量，此时用户消费电量符合市场规律。为刻画用户行为，引入经济学中的价格参考效应［5］，用户在进行购电决策时将当前电价与参考电价比较，当参考电价大于实际电价时，用户感觉“获利”，电力需求增加；当参考电价小于实际电价时，用户感觉“损失”，电力需求减少，则空调负荷需求模型为

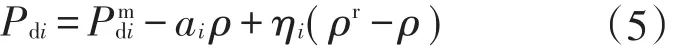
式中：ρ、ρr分别为空调负荷电价和参考电价，参考电价为历史电价的均值；Pmdi为最大空调功率；ai为价格敏感系数；ηi(ρr-ρ)表示实际电价与参考电价之差对电力需求的影响，ηi体现用户的行为偏好，这里引入经济学中行为偏好描述的3种类型：损失厌恶（loss averse）、损失中立（loss neutral）、风险喜好（gain-seeking）。则式（5）可改写为

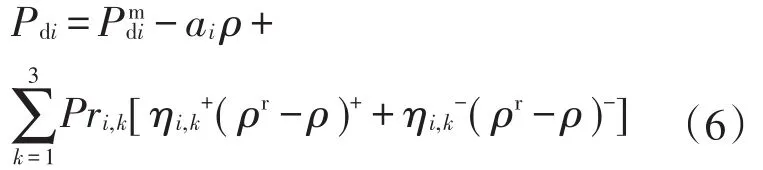
式中：(ρr-ρ)+=max{ρr-ρ,0}，(ρr-ρ)-=min{ρr-ρ,0}；ηi,k+为当参考电价大于实际电价时用户的偏好系数，ηi,k_为当实际电价大于参考电价时用户的偏好系数，ηi,k+和ηi,k_反映了电价波动对用户用电需求的影响；k=1,2,3分别表示用户类型为损失厌恶、损失中立、风险喜好，损失厌恶类型的用户对“损失”的敏感度大于“获益”的敏感度，即；风险偏好类型的用户对“损失”的敏感度小于“获益”的敏感度，即损失中立的用户对“损失”的敏感度等 于“ 获 益 ”的 敏 感 度 ，即Pri,k=(Pri,1,Pri,2,Pri,3)分别为用户i为损失厌恶型、损失中立型、风险喜好型的概率。

3 空调负荷代理商电力市场报价模型

空调负荷代理商电力市场报价模型如图2所示。

3.1 空调负荷代理商效用函数

采用效用函数来表示空调用户满意程度，负荷代理商的效用函数为其所代理的用户效用函数的集合。首先将式（6）改写为用户需求函数

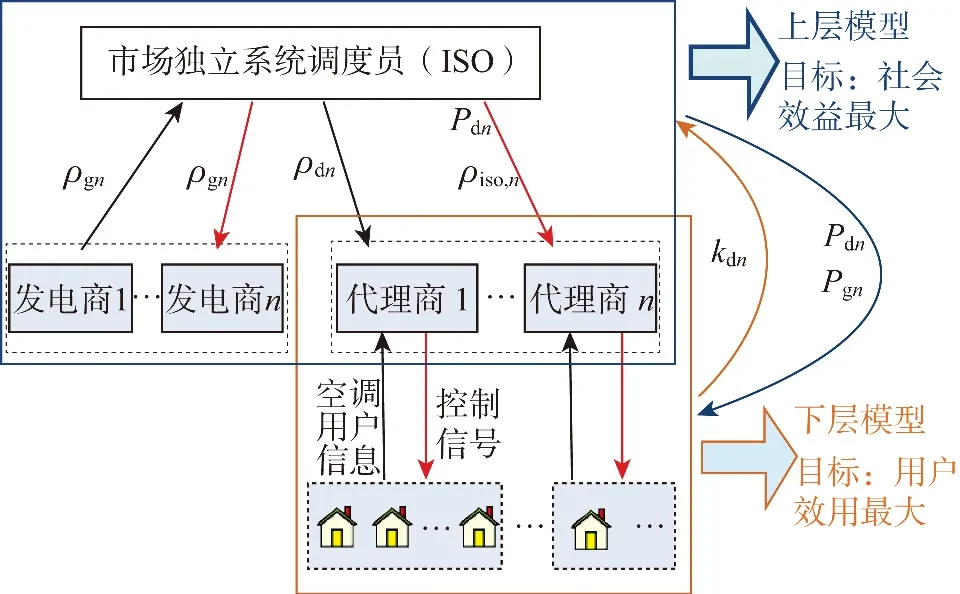
图2 双层模型具体结构

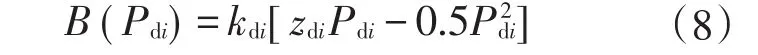
该效用函数包含了用户的特征信息，对于不同类型的用户，参数zdi和kdi均不同。代理商管理节点n上的空调，代理商的效用函数为

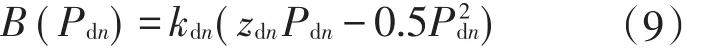
3.2 空调负荷代理参与市场竞价的双层模型

本文所提模型考虑系统ISO和用户代理商出清2个不同层面的优化问题。下层优化模型以用户代理商用电效益最大为目标

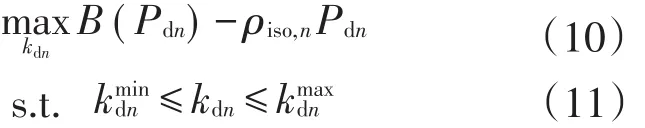
式中：Pdn为节点n的空调电量；ρiso,n为ISO在节点n的出清电价；报价参数kdn为决策变量。

上层定价主体ISO在满足电力网络安全运行约束下，以系统社会效益最大为调度目标，本文规定社会效益最大为用户用电效用最大，同时发电成本最小。为了使发电成本更具有现实性，同时引入常规发电的成本和新能源发电的成本，这里以风电作为新能源发电的代表。

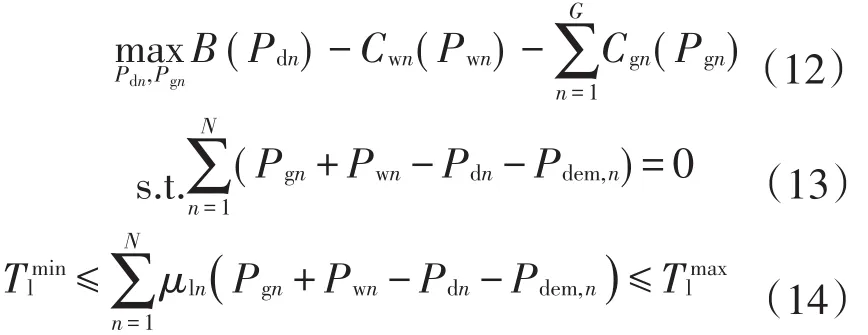
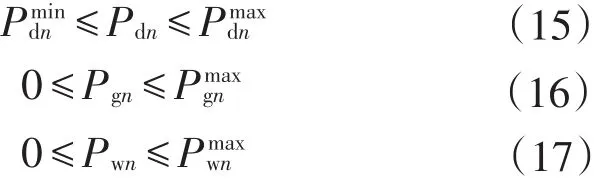
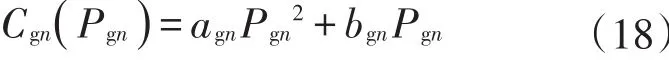
式中：agn、bgn分别为常规发电成本一次和二次系数。风电机组的发电成本包括3部分，即

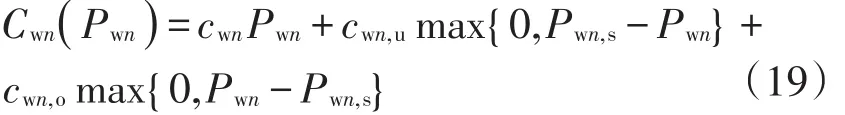
式中：Pwn,s为节点n的实际出力，为随机变量；Pwn为预测出力；cwn为风电机组直接发电成本系数；cwn,u、分别为风电功率低估和高估的惩罚成本系数；式（13）—（17）的拉格朗日乘子分别为均为非负数。

4 双层优化模型的计算

本文采用K-T法把双层优化问题转换成一个单层带平衡约束的数学优化模型（mathematical programs with equilibrium constraints,MPEC）［6］。通过KKT条件将上层优化模型转化为下列约束条件

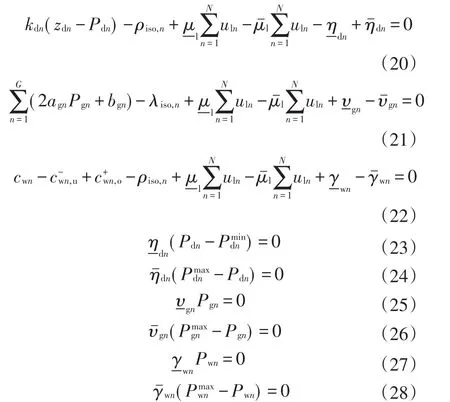
在上述约束式中，其中式（23）—（28）为非线性互补松弛条件，现把非线性问题转换成线性问题，过程如下：取足够大正数M、w为二元决策变量，对于互补性等式πf=0，其中π为拉格朗日系数，其值非负，f为一个受限制的连续函数（f≥0），可以通过M、w来对等式进行转化，π≤Mw，f≤M(1-w)。现将式（23）—（28）转换成线性不等式，转换结果如下

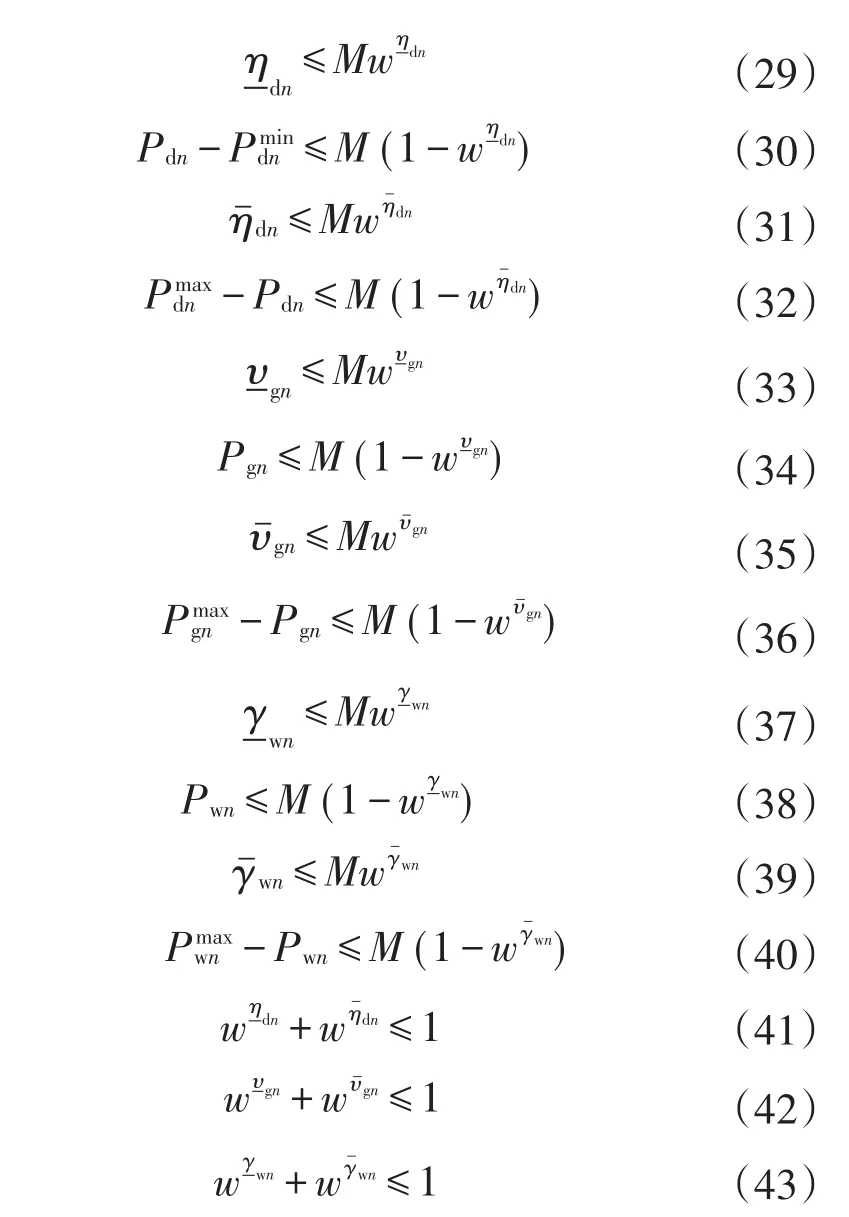
经上述转换后，双层非线性模型转化成单层线性模型

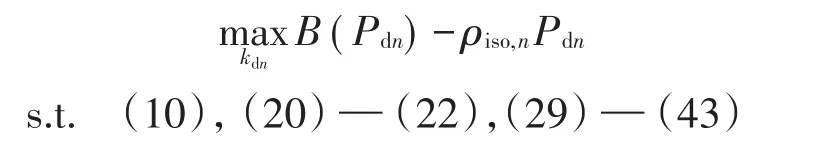
5 算例分析

双层模型转换成单层模型后，只需对单层模型进行求解，本文算例采用Matlab软件计算，通过Yalmip工具箱调用Cplex求解器进行求解。假设代理商所代理的用户空调负荷参数如表1，常规机组和风电的参数如表2和表3。假设在12:00～13:00时段室外温度恒定为36℃，为用电高峰时段，考虑人体的舒适度规定室温区间为［23℃，27℃］，根据式（1）—（3）求解负荷控制周期τc，以及空调的开启时间τon和关停时间τoff。

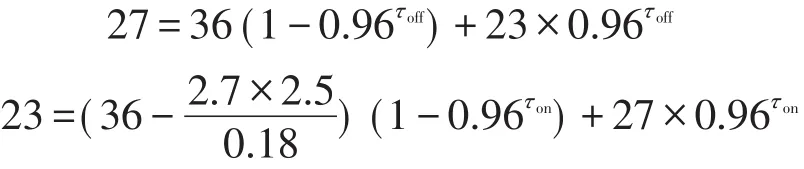
τoff=9min；τon=3.7min；τc=12.7min。由式（4）得出12:00～13:00时段的可控容量为

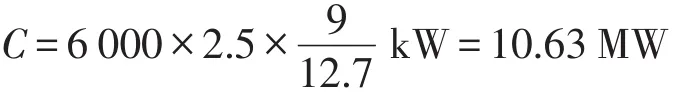
于是Pdn的范围为4.36 MW≤Pdn≤15 MW。

表1 空调负荷参数

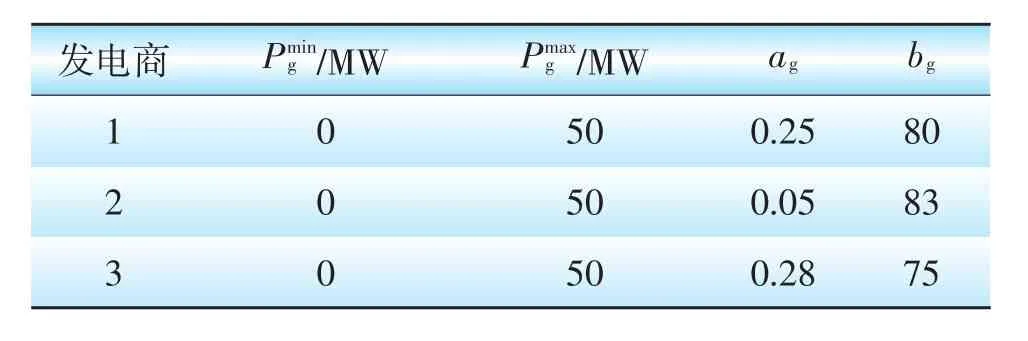
表2 发电机参数

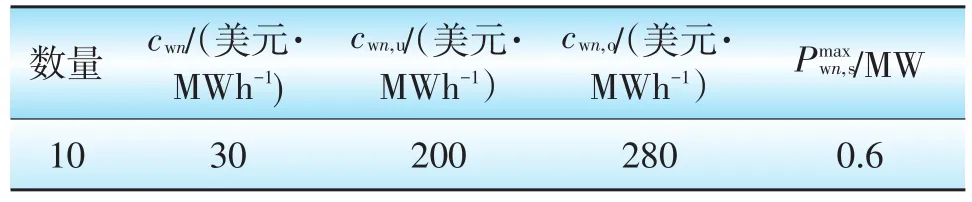
表3 风电机组参数

代理商向系统上报报价函数ρn=kdn(zdn-Pdn)，其中参考电价ρrn由PJM公司发布的数据节点RECO 2013年7—9月份实时电价数据取平均值得到，ρr=52美元/MW；假设代理商下辖的6 000个用户为同一种类型，代理商分别代理3种不同类型的用户情况下，类型1为损失厌恶型用户，η-=0.02,η+=0.01；类型2为损失中立型用户，η-=η+=0.015，类型3为风险喜好型用户,η-=0.01,η+=0.02，报价策略和削减负荷如表4。

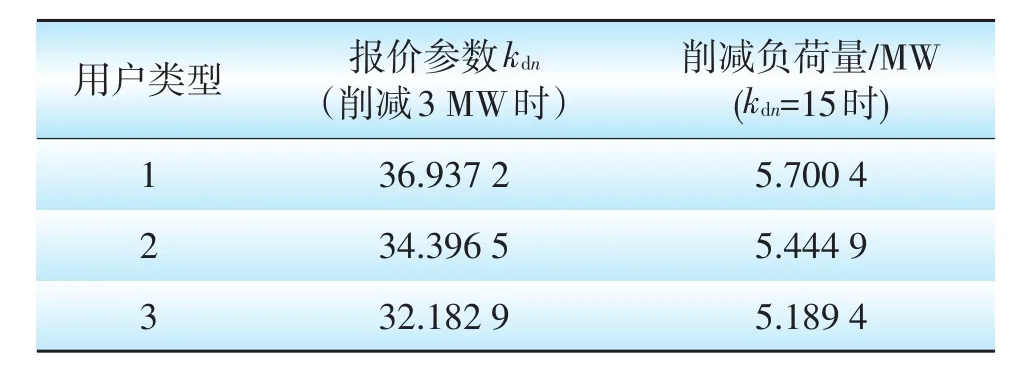
表4 不同用户类型下的报价策略和削减负荷的比较

代理商对于所管理的不同类型的用户，采取不同的报价策略。对于损失厌恶型的用户倾向于报较大的kdn，风险喜好类型的用户报较小的kdn，损失中立的用户居中；在相同的报价策略下，损失厌恶型的用户削减负荷最多，风险喜好型的用户削减负荷最少，而损失中立型的用户居中。

系统根据社会效益最大出清的电价与实时电价比较结果如表5，该模型下12:00～13:00电价为94.018 9美元/MWh，实时电价情况下，高峰电价均值为126.045 4美元/MWh，用户在该时段可减少电费32.026 5美元/MWh。算例结果表明，该模型一方面能充分考虑用户行为偏好，在不影响用户舒适度的前提下促进空调负荷积极参与市场竞价；另一方面使系统社会效益最大。

表5 有参与竞价与没有参与竞价时的电价比较美元/MWh

6 结束语

本文提出了空调负荷代理商参与市场竞价的双层优化模型，代理商在进行市场报价时，充分考虑用户的行为偏好，促进用户积极参与市场交易。通过KKT条件将双层优化模型转化为单层优化模型，采用非线性互补函数将非线性不等式约束转化为等式约束进行求解。最后对所提模型进行仿真分析，验证了本文模型的有效性和可行性，为空调负荷参与市场竞价提供了理论基础。D