引导电动汽车有序充放电的峰谷电价时段优化模型
2018-10-17许珊,李扬
许 珊,李 扬
(东南大学 电气工程学院,南京 210018)
电动汽车(electric vehicle,EV)是一种零排放或低排放的绿色交通工具[1],其大规模的推广能够有效缓解当今能源危机、环境污染等日益严峻的社会问题,因此受到社会各界的广泛关注。随着我国《电力发展“十三五”规划》等一系列国家鼓励政策的出台,电动汽车的用户保有量呈现出逐年增加的趋势,根据工业和信息化部发布的电动汽车发展战略研究报告,预计到2030年,我国电动汽车保有量将高达6 000万辆[2]。
在无外界调控的无序充电模式下,电动汽车的日充电负荷曲线主要受到车主的出行习惯和生活规律影响,与配电网日负荷曲线具有一致性[3—4],导致可能出现“峰上加峰”的情况,加重电网运行的负担。此外电动汽车还能够通过放电与电网进行双向互动,随着渗透率的增加,其无序充放电行为将会严重影响电力系统的正常的运行和规划[5],因此需要对其充放电行为进行一定的引导与控制。峰谷分时电价作为需求侧管理的重要手段,能够起到引导车主改变其充放电行为的作用[6],有必要对峰谷电价时段的优化进行研究。
文献[6]—文献[7]通过蒙特卡洛模拟得到电动汽车充电负荷的日负荷曲线,在此基础上建立了以峰谷差最小为目标的最优化模型并对峰谷电价时段进行寻优,实现了电动汽车的有序充电管理,但是文献没有考虑电动汽车向电网放电的因素,可能导致优化结果的适用性较弱。文献[8]综合考虑了电动汽车充放电的特点,通过改变电动汽车开始充、放电时刻和充、放电时长,对电动汽车进行有序的充放电控制。但是上述文献建立的峰谷分时电价方案仅仅考虑了电网侧的利益,忽略了对车主日常用电方式的影响,使得峰谷电价时段的设置有失公平[9]。因此,应引入用户满意度的指标以衡量电动汽车用户用电方式的变化量[9—11],使峰谷电价方案能够兼顾电网侧与用户侧的利益。
本文以电动私家车为主要研究对象,在利用蒙特卡洛仿真法建立规模化电动汽车充放电负荷模型的基础上,以峰、谷电价的开始时刻和持续时间为优化变量,建立引导电动汽车有序充放电的峰谷电价时段优化模型,并采用遗传算法对时段的设置方案进行寻优求解。通过峰谷电价对电动汽车充放电进行有效引导,达到统筹电网与用户双方利益的目的。
1 私家车出行习惯模型
1.1 模型假设
相比于公交车、出租车等电动车辆的行驶特性,私家车具有更大的可调控性,因此选择电动私家车作为主要研究对象。为了更好地分析电动汽车充放电行为对系统日负荷曲线的影响,对私家车主的出行习惯做如下简化:
(1)电动汽车通常采用“恒流-恒压”的充放电模式,恒流充放电时间较长,充放电时电池两级的电压几乎不变,因此将电动汽车的充放电视为恒功率过程[10]。
(2)在未实施峰谷电价的无序充放电情况下,电动汽车在最后一次出行返回后开始充电[11]。
(3)充放电功率、充放电开始时刻、日行驶里程是相互独立的随机变量。
(4)考虑到充放电深度、电池寿命和损耗等因素[12],设置车载电池可用电荷状态(state of charge,SOC)为10%~90%,SOC低于10%停止放电。
(5)私家车主在每次充电开始都已知电池充满电所需的充电持续时长。
(6)除峰谷分时电价外,不考虑其他外界因素对私家车主出行习惯的影响。
1.2 电动汽车日行驶里程
一般情况下,电动私家车的日行驶里程取决于用户的日常需要与行驶习惯,根据2001年美国交通部对全美家用车辆的调查结果(national household travel survey,NHTS)[13],电动汽车的日行驶里程近似服从对数正态分布,其概率密度函数如式(1)所示

式中:D为电动汽车日行驶里程,km;μD为日行驶里程期望值,μD=3.20;σD为日行驶里程标准差,σD=0.88。
电动汽车日行驶里程的概率分布如图1所示。
2 无序模式的V2G模型
2.1 无序充电模型
根据NHTS,无序模式下电动汽车最后一次出行返回时刻服从分段正态分布,根据1.1节的假设2,得到无序模式下充电开始时刻的概率密度函数,如式(2)所示
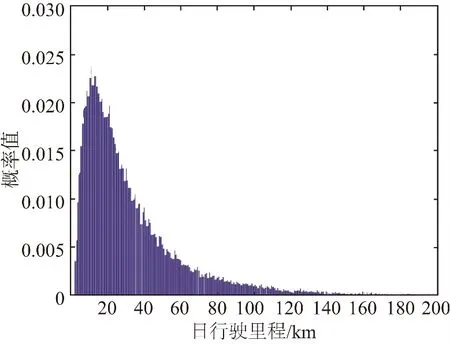
图1 电动汽车日行驶里程的概率分布
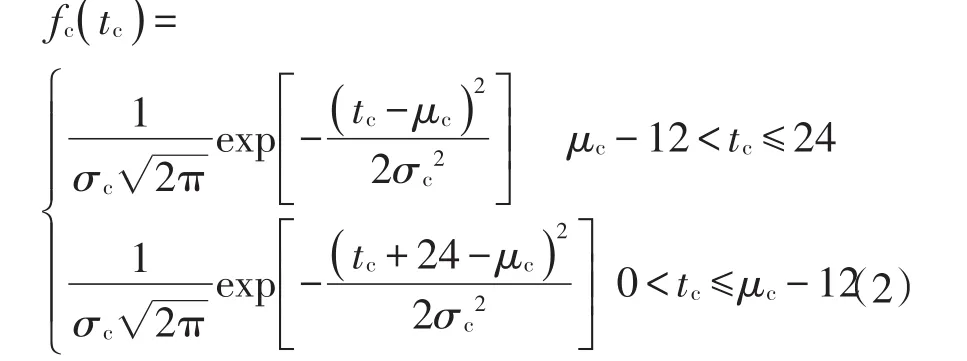
式中:tc为充电开始时刻;μc为充电开始时刻的期望值,μc=17.6;σc为充电开始时刻的标准差,σc=3.4。
根据1.1节中的假设1与假设5,得到如式(3)所示的电动私家车充电持续时长

式中:Tc,i为第i台电动私家车的充电持续时长,h;为电动私家车i的车载电池容量,kWh;Pc,i为其充电功率,kW。
2.2 无序放电模型
以一天为周期,假设电动私家车主早上9:00到达单位,下午16:00离开单位,即放电开始时刻为9:00到16:00。并且假设在无序模式下,电动汽车停放在单位期间的每个时刻的放电概率相同,即放电开始时刻服从满足均匀分布,因此得到放电开始时刻的概率密度函数,如式(4)所示
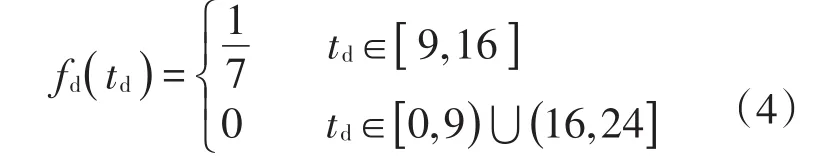
式中:td为放电开始时刻。在9:00到16:00电动私家车放电概率为1/7,其余时间放电概率为0。
放电持续时长与车载电池容量、日行驶里程、每千米电耗量以及放电功率有关,因此得到放电持续时长如式(5)所示
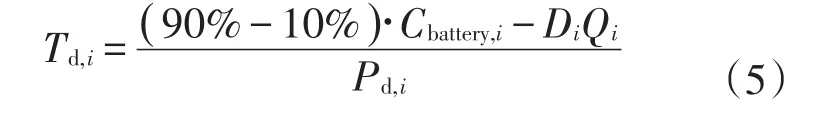
式中:Td,i为电动私家车i的放电时长;Di为电动私家车i的日行驶里程;Qi为每千米电耗量;Pd,i为放电功率。
3 有序模式的V2G模型
3.1 峰谷电价模型
峰谷分时电价是实现电力需求侧管理的有效措施,通过电价引导用户的用电行为,改变原有的负荷曲线,使部分高峰负荷转移至用电低谷期,从而实现削峰填谷、保障供电可靠性的目的[7]。峰谷电价数学模型如式(6)所示

式中:prv、prp、prf分别为谷电价、峰电价和平电价,且 prv<prp< prf;tv1、tv2分别为谷电价开始时刻和谷电价结束时刻;tp1、tp2分别为峰电价开始时刻与峰电价结束时刻;其余时间执行平电价。
定义峰谷电价响应度η表示有序充放电,即在谷电价时段充电、峰电价时段放电的电动私家车占电动汽车总数的比例。计算公式如式(7)所示

式中:n为响应峰谷电价的电动私家车数量;N为研究区域内电动私家车总数量。
3.2 有序充电模型
假设电动私家车的日行驶里程不随峰谷电价政策而改变,已知电动私家车i所需的充电时长Tc,i,为了尽可能在谷电价时段充电以降低充电费用,响应峰谷电价的车主的开始充电时刻为
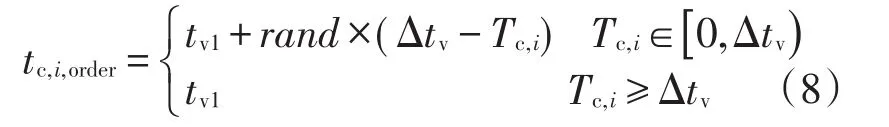
式中:tc,i,order为电动私家车i在峰谷电价模式下的开始充电时刻;rand为[0,1]区间的一个随机数;Δtv为谷电价持续时长,Δtv=tv2-tv1。
式(8)表示,在有序充电模式下,电动私家车主为了尽可能降低充电费用,当其所需充电时长小于谷电价持续时长时,充电开始时刻应能保证其充电的全过程处于谷电价区间内;反之,车主应从谷电价开始时刻开始充电。
3.3 有序放电模型
已知电动私家车i所需的放电时长Td,i,为了尽可能在峰电价时段放电以获得更多的放电收益,响应峰谷电价的车主的开始放电时刻为
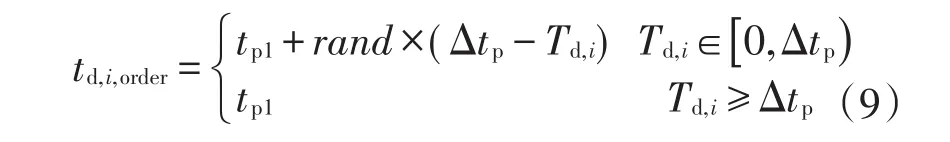
式中:td,i,order为电动私家车i在峰谷电价模式下的开始放电时刻;Δtp为峰电价持续时长,Δtp=tp2-tp1。
式(9)表示,在有序放电模式下,电动私家车主为了获取尽可能多的收益,当其所需放电时长小于峰电价持续时长时,放电开始时刻应能保证其放电的全过程处于峰电价区间内;反之,车主应从峰电价开始时刻开始放电。
4 最优峰谷电价时段划分模型
4.1 模型建立
为了充分协调电网与用户双方的利益关系,设定如式(10)所示的综合指标作为目标函数
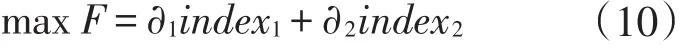
式中:∂i(i=1,2)为权重系数,根据实际需要进行设置,∂1+∂2=1;indexi为各项指标,具体公式如下。
(1)index1:峰谷差率改善度指标,用于衡量电动汽车有序充放电对负荷曲线的改善效果
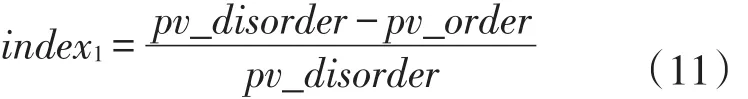
式中:pv_disorder为电动私家车无序充放电的峰谷差率;pv_order为实施峰谷电价方案后的峰谷差率。
(2)index2:用电方式满意度指标,用于衡量峰谷电价实施前后电动私家车主用电量在时间轴上的变化程度[11],变化程度越小,满意度越高。在实施峰谷电价政策之前,车主完全根据自己的用电习惯进行充放电操作,此时用电方式满意度最大。实施峰谷电价后,参与响应的车主为了降低电费而改变其原本的充放电习惯,这相当于在一定程度上限制了车主的用电自由,影响用户用电方式满意度

式中:loadt,0为未实施峰谷电价的无序模式下电动汽车在t时刻的负荷;loadt,order为峰谷电价实施后的有序充电模式下电动汽车在t时刻的负荷。
约束条件包括谷电价开始时刻约束、峰电价开始时刻约束、谷电价持续时间约束、峰电价持续时间约束等。
因此,以峰谷电价开始时刻以及持续时间为变量、以统筹电网与车主利益的综合指标为目标函数的最优峰谷电价时段划分模型如式(13)所示
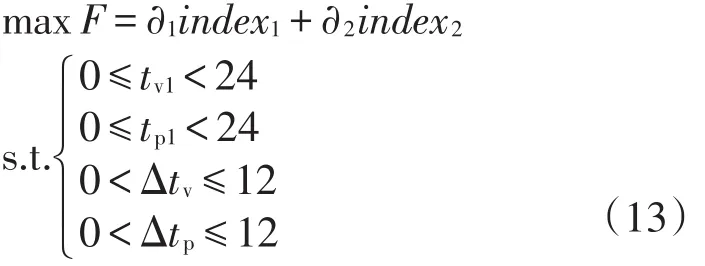
4.2 求解方法
4.2.1 蒙特卡洛模拟法
蒙特卡洛模拟法是一种采用随机抽样来估算数学函数的计算方法。利用蒙特卡洛模拟法来模拟电动私家车主的出行习惯和用电方式,计算规模化电动汽车的充放电负荷。实施峰谷电价的有序充放电模式下,利用蒙特卡洛法仿真系统负荷的具体步骤如下:
(1)设置峰谷电价响应度η,电动汽车数量N=400辆,蒙特卡洛迭代次数M=100次。
(2)对第i辆电动私家车,随机抽取其类型、充放电功率。
(3)产生满足式(1)的概率密度分布的日行驶距离。
(4)峰谷电价模式下,有ηN辆电动汽车参与响应,(1-η)N辆电动汽车不参与响应,因此判断该辆电动汽车是否参与响应。
(5)参与响应则按照有序模式进行充放电,否则按照无序模式进行充放电。
(6)遍历所有电动汽车,叠加其充、放电功率,从而得到规模化的电动汽车充、放电负荷曲线L1(t),L2(t)。
(7)与系统基础负荷叠加,得到一天24 h的负荷曲线L(t),t=1,…,24。
(8)为保证计算精度,蒙特卡洛共模拟M次,将M次结果取平均值作为最终的结果。
4.2.2 遗传算法
遗传算法是解决优化问题的常用方法之一。以(tv1,Δtv,tp1,Δtp)为变量和输入参数,利用遗传算法进行寻优,得到最优综合指标下的最优峰谷电价时段设置结果以及优化后的系统负荷曲线。具体步骤如下:
(2)判断生成的种群是否满足式(13)中的约束条件,若不满足,则丢弃次种群;
(3)计算系统负荷;
(4)以式(10)的综合指标作为目标函数并计算适应度大小;
(5)采用轮盘赌法对父本进行选择;
(6)对选择出的父本通过交叉与变异操作产生新种群,其中交叉概率Pc=0.8,变异概率Pm=0.1;
(7)反复迭代寻优,直至达到最大迭代数或满足精度要求,输出最优峰谷电价时段划分等计算结果。
5 算例分析
为验证上述算法及优化模型,以国内某地区为例进行算例分析。假设该地共有500辆电动私家车,电动私家车具体参数如表1所示。
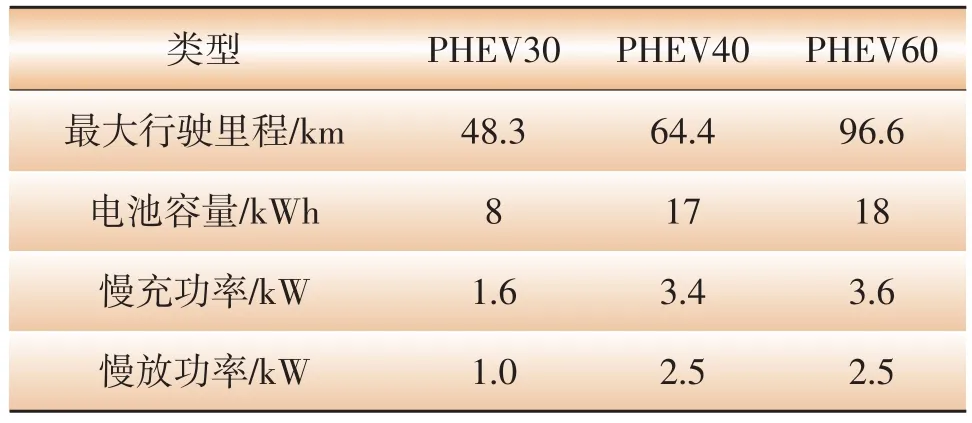
表1 电动汽车参数
以该地典型日负荷数据为基础负荷,在没有实施峰谷电价的情况下,模拟电动私家车无序充放电曲线,与基础负荷叠加,形成了电动汽车接入电网无序充放电后的系统负荷曲线。在此基础上,利用K均值聚类可以划分出峰谷时段,如图2所示,得到峰时段为18:00至22:00,谷时段为0:00至8:00。
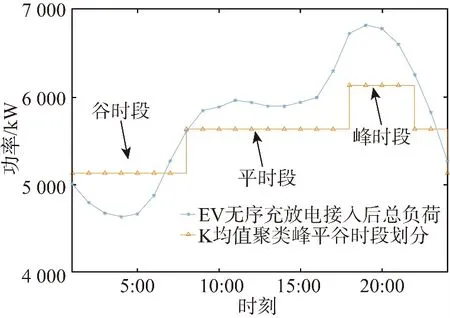
图2 K均值聚类的峰谷时段
考虑综合指标的目标函数的权重设置为∂1=0.5,∂2=0.5;峰谷电价响应度η=0.7。在Matlab编程环境下对电动汽车有序充放电的最优峰谷电价时段划分进行优化。通过优化计算,得到当响应度η=0.7时,峰谷电价时段的最优设置方案如表2所示,基础负荷曲线、无序模式下的日负荷曲线以及实施优化峰谷电价时段方案的日负荷曲线如图3所示。K均值聚类峰谷时段方案与优化方案的各项指标对比如表3所示。

表2 峰谷电价时段优化方案
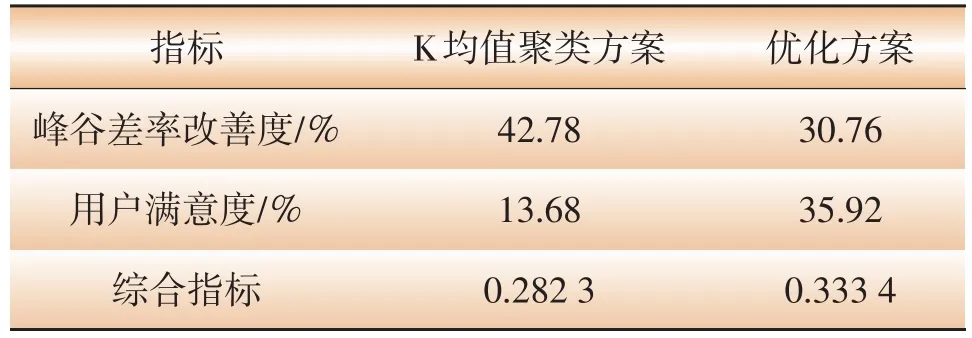
表3 2种峰谷时段方案对比
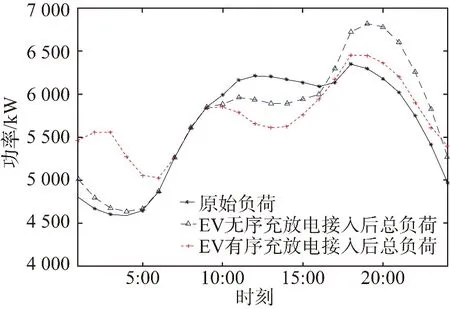
图3 峰谷电价时段优化前后的负荷曲线
由图3可见,电动汽车在无序充放电的模式下接入电网,在电动私家车主日常出行习惯和生活规律的影响下,日最大负荷由6 353.25 kW增加到6 821.72 kW,增长了7.37%,峰谷差由1 763.33 kW增加到2 188.37 kW,增长了24.10%,峰谷差率由27.75%增长为32.08%,增长了15.60%。电动汽车的无序充放电拉大了峰谷差,使电网出现了“峰上加峰”的情况,这无疑增加了电网的负担,威胁电网的可靠运行。
实施表2所示峰谷电价时段后,电动汽车的充放电行为得到了有效的调控,日最大负荷由6 817.20 kW减小到6 454.73 kW,减小了5.32%,峰谷差由2 188.37 kW降低到1 430.45 kW,减小了34.63%,峰谷差率由32.08%降低到22.16%,减少了30.92%。电动汽车的有序充放电减小了峰谷差,达到了削峰填谷的目的。
通过表3中2种峰谷时段方案的各项指标对比可见,虽然基于K均值聚类的峰谷时段划分方案能够显著地降低系统峰谷差(峰谷差率改善度为42.78%,比优化方案高出39.08%),但是车主用电方式满意度仅为13.68%,导致其综合指标较低,为0.282 3,而峰谷电价时段优化方案的车主用电方式满意度为35.92%,其综合指标为0.333 4,总体优于K均值聚类方案。由此可见,通过优化峰谷电价时段引导电动汽车有序充放电,能够在保持电动私家车主用电方式满意度的同时,起到改善负荷曲线的作用,较好地统筹了电网与用户双方的利益。
6 结束语
在电动汽车车主出行习惯与生活规律的影响下,电动汽车的日充电负荷曲线与电网日负荷曲线具有一致性,因此电动汽车的无序充放电可能导致电网出现“峰上加峰”的情况。
为了有效引导电动汽车进行有序充放电,本文以电动私家车为研究对象,建立了基于峰谷电价的电动汽车有序充放电模型,并提出了考虑峰谷差率改善度、用户用电方式满意度的综合指标为优化目标的优化模型,采用遗传算法得到了最优峰谷电价时段设置方案。将优化方案与K均值聚类峰谷时段方案进行对比,结果表明,优化方案能够较好的兼顾电网与用户双方的利益,既能保证用户用电方式满意度,又能减小电网负荷峰谷差。D
