键槽梁底筋锚入式预制梁柱连接恢复力模型

管东芝 郭正兴 杨 辉 杨 森

(东南大学土木工程学院, 南京 210096)(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)

在我国建筑业转型升级的新形势下，装配式混凝土结构契合建筑产业现代化的内涵，成为我国新型建筑工业化发展的重要方向和突破点.国务院已明确提出大力推广装配式建筑，力争用10年时间，使装配式建筑占新建建筑的比例达到30%[1].框架结构的梁、柱等构件适于模数化、标准化和定型化，更加符合预制生产、运输和吊装的要求，使得装配式混凝土框架结构具有明显的推广应用优势，成为行业关注的热点[2].

目前，国内建造的装配式混凝土框架结构主要包括预制梁底筋锚入式、梁端键槽搭接式以及节点整体预制式等体系.这些体系往往存在着加工精度要求高、适用性不足、施工建造不便、抗震性能不理想等问题，大大抵消了装配式混凝土框架的应用优势[3].因此，开发和研究结构性能良好、具有规模化应用潜力的装配式混凝土框架结构体系具有重要的学术研究意义和重大的工程应用价值.

结构恢复力模型是结合理论分析和试验结果数据进行抽象简化而来的本构关系模型.它适用于对结构进行计算分析，能够反映构件在反复荷载作用下的滞回特点以及强度、刚度、延性等关键力学特征.在工程结构计算时，往往通过理论或试验方法确定构件的恢复力模型，再采用非线性有限元方法分析结构在地震荷载作用下的内力和变形.因此，恢复力模型是了解和确定结构抗震性能的重要基础和依据，计算简单实用，具有较高的应用性[4-5].

为提高装配式混凝土框架结构的建造优势,文献[6-7]提出了2种新型键槽梁底筋锚入式预制梁柱连接，并进行了低周反复试验研究，显示出较好的抗震性能和应用前景.本文针对这2种连接形式开展理论研究，并基于试验结果，建立了相应的恢复力模型，为结构弹塑性分析和抗震设计提供参考.

1 键槽梁底筋锚入式预制梁柱连接

键槽梁底筋锚入式预制梁柱连接的提出旨在降低装配式混凝土结构现场施工的难度，提高构件安装效率，减少建造总成本，同时保证良好的抗震性能，促进装配式混凝土框架结构的推广应用.基本形式主要有2种：①锚固与附加钢筋搭接混合连接；②部分高强筋预制装配式框架梁柱连接.

锚固与附加钢筋搭接混合连接形式见图1.该连接形式采用“大直径、少根数”的构造思路，增大预制梁底部伸出钢筋的直径，减少底部伸出钢筋的数量，加大钢筋之间的距离，从而减小伸出钢筋互相碰撞和干扰的概率.该连接中，预制叠合梁端留有U形键槽，梁下部仅保留2根粗钢筋从键槽底壁伸出.构件吊装时，粗钢筋伸入节点核心区进行锚固，附加U形钢筋设置于连接区.吊装完成后，通过现场叠浇混凝土来形成整体连接.

(a)预制构件

(b)整体连接

部分高强筋预制装配式框架梁柱连接形式如图2所示.该连接形式采用“高强度、小直径”的构造思路，梁底筋采用12，14，16 mm的小规格600 MPa级热处理带肋高强钢筋.小规格钢筋在梁端U形键槽内能够现场通过人工进行适当的侧向弯曲，避开碰撞的钢筋，从而适应施工现场复杂的状况，提高现场施工的容差性和普适性，降低建造难度，提升生产施工的效率.根据受力需要，可设置单层或双层钢筋锚固于节点核心区内.为提高键槽区下部混凝土承载力及变形能力，在梁端键槽内部增设环绕高强筋的小型矩形封闭箍筋，形成内部芯梁.

(a)单层高强筋

(b)双层高强筋

2 骨架曲线

钢筋混凝土结构的荷载-变形曲线模型主要包括曲线型模型和折线型模型.在实际工程中，由于折线型模型构成简单、操作性强，应用较为广泛.根据考虑因素的不同，折线型模型可分为二折线型、三折线型和四折线型模型.本文根据试验结果曲线的特点[6-7]，采用应用较广的平顶三折线型模型(见图3).该模型的关键点主要包括屈服点和峰值点，分别对应屈服强度Py、峰值强度Pmax、屈服变形Δy和峰值变形Δu.

图3 平顶三折线型模型

2.1 强度计算

键槽梁底筋锚入式预制梁柱连接采用等同现浇设计原则，试验中未发生明显的预制混凝土与后浇混凝土界面之间的滑移，且最终破坏形式均为梁铰机制破坏，故可认为平截面假定适用于该连接，采用“强柱弱梁”原则设计的键槽梁底筋锚入式预制梁柱连接的强度受梁截面控制.

计算连接节点屈服强度时，以梁截面最外层受拉钢筋屈服作为试件屈服的标志，根据“平截面”假定来计算混凝土和钢筋的应变分布，其中混凝土应变按照三角形分布，根据截面内力平衡来计算混凝土受压区高度，进而得出截面各部分的应变值.对于锚固与附加钢筋搭接混合连接和部分高强筋预制装配式框架梁柱连接而言，由于第2层钢筋分别为附加U形钢筋和锚入节点核心区的芯梁上部骨架筋，相对于最下层受拉筋往往截面积较小，为方便计算，下部钢筋受拉时的截面屈服弯矩可直接通过截面压力对最下层受拉钢筋中心取矩求得.当下部钢筋受压时，考虑下部第2层钢筋的受压作用进行屈服强度计算.

峰值强度计算模型依据《混凝土结构设计规范》(GB 50010—2010)[8]，采用混凝土等效矩形应力分布计算方法.计算时假定受压区钢筋屈服，若计算求得的受压区有效高度小于受压区钢筋至受压混凝土边缘距离的2倍，则说明假定不成立，此时试件峰值强度应通过受拉钢筋极限力对受压钢筋中心取矩求得.

2.2 变形计算

文献[6-7]指出，节点核心区设计较强时，试验中基本无损伤，变形极小.为简化计算，本文忽略该部分变形量.此时认为预制混凝土梁柱节点连接的总变形Δt主要由梁柱交接面张开变形Δo、柱受弯变形Δc和梁受弯变形Δb组成.其中，梁柱交接面张开变形是考虑锚固钢筋向节点区应力渗透的影响而进行的简化等效[9].变形组成示意图见图4.图中，l为加载点至梁柱交接面的距离；P为施加的荷载；le为受拉钢筋节点区锚固长度；Mc为柱受到的弯矩；h0为梁截面有效高度；hc为柱截面高度；Lp为塑性铰长度.

梁柱交接面张开变形为[9]

(a)梁柱交接面张开变形

(b)柱受弯变形

(c)梁受弯变形

(1)

柱受弯变形导致的梁端位移为[9]

(2)

式中，fs为最外层受拉钢筋强度，计算屈服位移和峰值位移时分别取屈服强度和峰值强度；Es和Ec分别为钢筋和混凝土弹性模量；Ic为柱等效截面惯性矩.

梁受弯变形导致的屈服位移根据屈服强度、截面等效抗弯刚度与变形的关系进行计算，峰值位移计算公式为[10]

Δb=Δy+(φu-φy)Lp(l-0.5Lp)

(3)

式中，φc和φy分别为梁根部峰值和屈服阶段的曲率，通过强度和截面等效抗弯刚度计算得到.计算峰值强度时，由于混凝土破碎严重，截面等效抗弯刚度近似仅考虑受压和受拉钢筋截面.

2.3 计算结果

计算屈服强度时，以梁截面最外层受拉钢筋屈服应变作为基本参数来计算梁截面屈服弯矩.而实际工程中，钢筋混凝土构件截面上的不同位置存在着钢筋和混凝土，最外层受拉钢筋屈服临界点不能代表整体构件均进入屈服阶段，导致2.1节中的假定会导致计算得到的构件理论屈服强度偏小.因此，将屈服强度的计算结果提高5%，作为键槽梁底筋锚入式预制梁柱连接的理论屈服强度值.在计算峰值强度时，若受压钢筋较多，为便于计算，采用钢筋极限强度来确定峰值弯矩；而实际上，钢筋达到极限强度被拉断的情况较混凝土破碎导致破坏的情况少.采用钢筋极限强度来计算构件峰值强度时，建议将计算峰值强度降低5%作为键槽梁底筋锚入式预制梁柱连接的理论峰值强度值.为简化计算，假定梁正向和反向同时达到屈服和峰值强度，取正向和反向强度值之和作为梁柱中节点构件的强度值.

将文献[6-7]中的试件尺寸、配筋及材料强度带入上述计算模型中进行计算，并与试验骨架曲线进行比较，结果见图5.图中，S2和S3为锚固与附加钢筋搭接混合连接试件；S4和S5为部分高强筋预制装配式框架梁柱连接试件.由图可知，理论计算结果与试验骨架曲线具有较好的吻合度，可基本反映2类预制梁柱连接试件受力和变形的各阶段特征和数值大小.

3 滞回规则

(a)试件S2

(b)试件S3

(c)试件S4

(d)试件S5

确定恢复力模型的骨架曲线后，需要根据试验数据确定简便合理的滞回规则，从而建立理想的恢复力模型.

3.1 滞回路线

考虑键槽梁底筋锚入式预制梁柱连接的特点，滞回路线通过加、卸载刚度确定.基本恢复力模型示意图见图6.

由图6可知，OA和OA′为正向和反向的弹性段.当加载位移角未超过屈服位移角时，试件处于弹性阶段，加载和卸载刚度均采用与骨架曲线弹性段相同的刚度.当加载位移角超过屈服位移角后，节点构件的正反向荷载-变形关系沿骨架曲线OABC和OA′B′C′进行.构件进入屈服状态后，正向卸载时沿ab以正向卸载刚度k1进行卸载；正向卸载完成后，沿bc以反向加载刚度k2进行反向加载；与反向骨架曲线相交后，再以卸载刚度k3沿de进行反向卸载；反向卸载完成后，以正向加载刚度k4沿ef进行再加载.按照上述步骤往复进行.

图6 基本恢复力模型示意图

3.2 刚度拟合

由滞回路线可知，正向卸载刚度k1、反向加载刚度k2、反向卸载刚度k3和正向加载刚度k4为滞回路线中的关键参数，需采用文献[6-7]中的低周反复荷载试验结果进行拟合，以确定加、卸载刚度与位移角的关系.

将预制试件每级加载第1次循环的滞回曲线分成3个部分：①正向峰值点到正向卸载点部分；②正向卸载点到反向峰值点部分；③反向峰值点到反向卸载点部分.同时，将该级第3次循环的反向卸载点至下一级峰值点的部分作为第4部分，分别对应着正向卸载刚度k1、反向加载刚度k2、反向卸载刚度k3和正向加载刚度k4.其中，卸载点为荷载-变形曲线上荷载降为零时对应的点.通过线性拟合的方式得出拟合直线的斜率，作为滞回路线中各部分刚度的基本试验数据.由试验骨架曲线的特征可知，各试件大致在1%位移角时屈服.为减少试件屈服的影响，将试验骨架曲线中0.75%位移角之前的部分作为试件的弹性阶段，通过线性拟合确定这部分的斜率，作为各试件的初始刚度值k0.试件S2～S5的初始刚度值k0分别为61.726，56.716，55.893，51.487 GN·m.各阶段刚度值见表1.

表1 试件各阶段刚度值 GN·m

文献[11-13]指出，通过试验数据进行刚度比(各阶段刚度与初始刚度之比)与变形比(加载变形与标志变形值之比)的拟合较为常见.采用0.75%位移角作为标志变形值，对试件各阶段刚度之比与位移角之比进行自然指数关系拟合，结果见图7.由图可知，拟合曲线与试验结果相关系数平方值R2分别为0.964 1，0.938 7，0.950 5，0.944 7，拟合效果较好.

4 恢复力模型

以第2节中的静力计算模型计算结果作为试件理论骨架曲线，采用第3节中的滞回路线和各阶段刚度计算式，建立键槽梁底筋锚入式预制梁柱连接的恢复力模型.计算时初始刚度采用理论骨架曲线弹性段刚度，标志位移角采用理论屈服位移角.各预制试件的恢复力模型计算曲线与试验滞回曲线对比见图8.

由图8可知，建立的恢复力模型计算结果与试验滞回曲线具有良好的吻合度.该模型可模拟键槽梁底筋锚入式预制梁柱连接试件在低周反复荷载作用下加载、卸载、再加载的弯矩与位移角关系特征，较好地反映了试件的抗震特性，可用于该形式的预制梁柱连接构件或结构弹塑性分析.

(a)k1

(b)k2

(c)k3

(a)试件S2

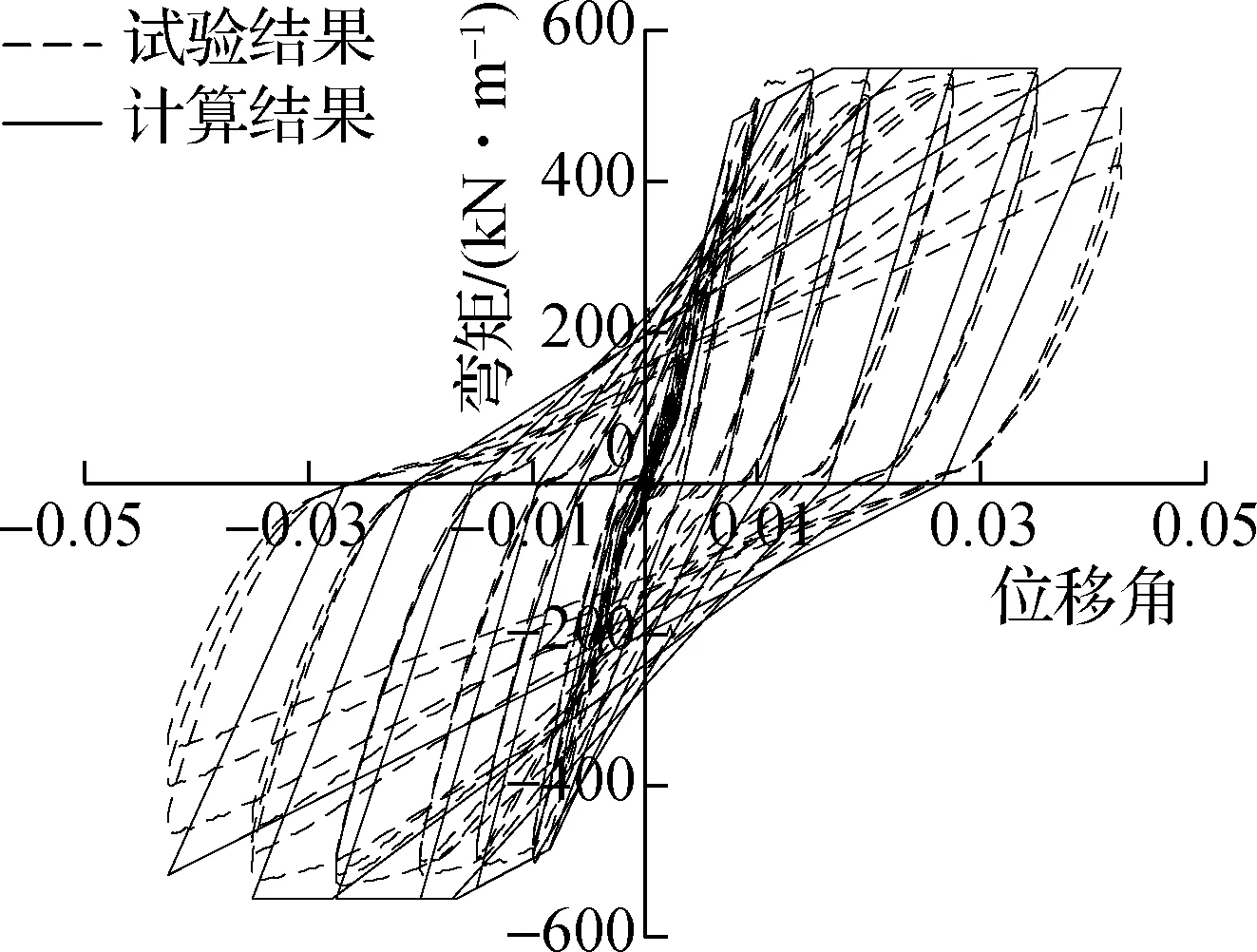
(b)试件S3

(c)试件S4

(d)试件S5

5 结论

1)从“大直径、少根数”和“高强度、小直径”的思路出发，形成2种键槽梁底筋锚入式预制梁柱连接形式，降低了生产和施工难度，提高了建造效率，有效保证了结构性能，具有较好的应用前景.

2)基于平截面假定的强度计算方法适用于键槽梁底筋锚入式预制梁柱连接；将构件变形分解为梁柱交接面张开变形、柱受弯变形和梁受弯变形的计算方法可用于节点核心区较强的键槽梁底筋锚入式预制梁柱连接试件.形成的三折线理论骨架曲线与试验结果具有较好的吻合度，基本反映了2类键槽梁底筋锚入式预制梁柱连接受力和变形特征和数值大小.

3)将试验结果的滞回曲线各阶段进行拟合，得到曲线刚度值.基于试验刚度值拟合得到试件在低周反复加载试验中的各阶段刚度与位移角关系，拟合曲线与试验结果相关系数平方值分别为0.964 1，0.938 7，0.950 5，0.944 7，拟合效果较好.

4)结合理论计算的骨架曲线建立的恢复力模型计算结果与试验滞回曲线吻合较好，可用于键槽梁底筋锚入式预制梁柱连接的弹塑性分析及抗震设计.