级间耦合刚度对两级行星传动系统啮合动载荷的影响分析

李剑英，朱天军，宗长富，许志勇，胡青春

（1.肇庆学院 机械与汽车工程学院，广东 肇庆 526061；2.肇庆学院 电子与电气工程学院，广东 肇庆 526061；3.华南理工大学 机械与汽车工程学院，广东 广州 510640）

0 前言

新能源汽车采用内燃机、发电机/电动机作为动力源时，为解决这种多动力源耦合问题，常采用行星传动机构作为其传动系统的关键零部件[1-2]，然而，行星传动机构的振动和噪声一直是影响系统性能的关键因素.尽管学术界已针对该类传动的动态特性问题进行了广泛研究，主要涉及动力学建模和动态响应求解等[3-4]，但在建立动力学模型时均将齿轮和行星架视为刚体，有学者指出，若行星传动机构内齿圈采用薄壁结构，内齿圈弹性对传动系统动态特性的影响在某些特定场合应被涉及[5-8].由于内齿圈采用薄壁结构，在传动过程中发生的显著变形将对传动系统的动态特性具有较大影响，如文献[9]作者采用多尺度摄动方法，对单级弹性内齿圈行星传动非线性动力学特性进行了研究.针对多级行星传动线性动力学特性（视各级内齿圈为刚体），国内学者[10-12]对盾构机刀盘驱动行星齿轮系统的动态特性进行了分析；秦大同等[13-14]对风电发电机行星传动系统的动态特性进行了广泛研究，而对计入内齿圈弹性的两级行星传动动力学研究尚未见报道.

求解行星齿轮传动系统动力学方程的方法主要有解析法和数值法，其中解析法一般是对解的近似表达式进行求解，常见的有多尺度摄动法和谐波平衡法等，而数值法主要有Runge-Kutta法和Gill法等.因计入了内齿圈的弹性，除增加弹性内齿圈的运动微分方程外，内齿圈与行星轮的啮合作用力及其反作用力项亦发生了改变，同时视弹性内齿圈的支承为切向和径向刚度约束的弹性结构，并考虑两级行星传动构件间的耦合刚度，这些因素不仅在求解传动系统的运动微分方程时带来一定困难，而且对其动态特性产生影响.为深入分析级间耦合刚度对弹性支承下薄壁内齿圈两级行星传动系统动态特性的影响，本文基于所建立的刚柔耦合混合动力学微分方程，考虑两级齿轮副时变啮合刚度，运用Runge-Kutta法对弹性支承薄壁内齿圈两级行星传动系统啮合动载荷进行深入分析，旨在揭示级间耦合刚度变化对传动系统动态特性的影响规律，为后续行星传动系统的性能优化及减振降噪提供理论依据.

1 弹性支承薄壁内齿圈两级行星传动系统动力学微分方程[15-18]

某混合动力系统的双离合两档行星齿轮机构由行星排第Ⅰ级、第Ⅱ级，离合器c1,c2以及壳体组成[16].第Ⅰ级和第Ⅱ级太阳轮固连在一起，它们间的耦合刚度以表示；第Ⅰ级内齿圈与第Ⅱ级行星架固连，它们间的耦合刚度以表示，离合器c1可对rⅠ与cⅡ的组合进行离合；离合器c2可对rⅡ进行离合，行星架cⅠ为输入端，太阳轮组sⅠ-sⅡ为输出端.基于动力学建模所做的假设[15-17]，各级行星传动均以各自行星架随动坐标系为参照系，为便于描述，本文约定，i=Ⅰ,Ⅱ分别表示第Ⅰ级和Ⅱ级行星传动；n=1,2,…,Ni,其中NⅠ,NⅡ代表第Ⅰ级和第Ⅱ级行星传动的行星轮个数.在第Ⅰ级行星传动平移-扭转动力学模型基础上，考虑第Ⅱ级行星传动内齿圈弹性变形和弹性基的约束，通过级间耦合的方法得到两级行星传动动力学模型（图1所示）.在行星传动动力学模型中分别表示第i级构件h的平移和扭转微位移，为第i级构件h产生的角位移，且其中为第i级构件h的基圆半径（为第i级行星轮中心所在圆的回转半径）；分别表示第i级行星轮n的平移和扭转微位移；u(θ,t)为第Ⅱ级内齿圈的切向位移，若不做特别说明，本文一律将u(θ,t)简写为u.

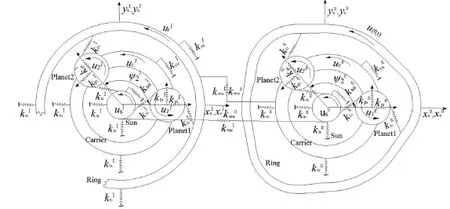
图1 弹性支承下的薄壁内齿圈两级行星传动系统动力学模型[18]

依据牛顿第二定律建立第Ⅰ级、第Ⅱ级行星传动的动力学微分方程.

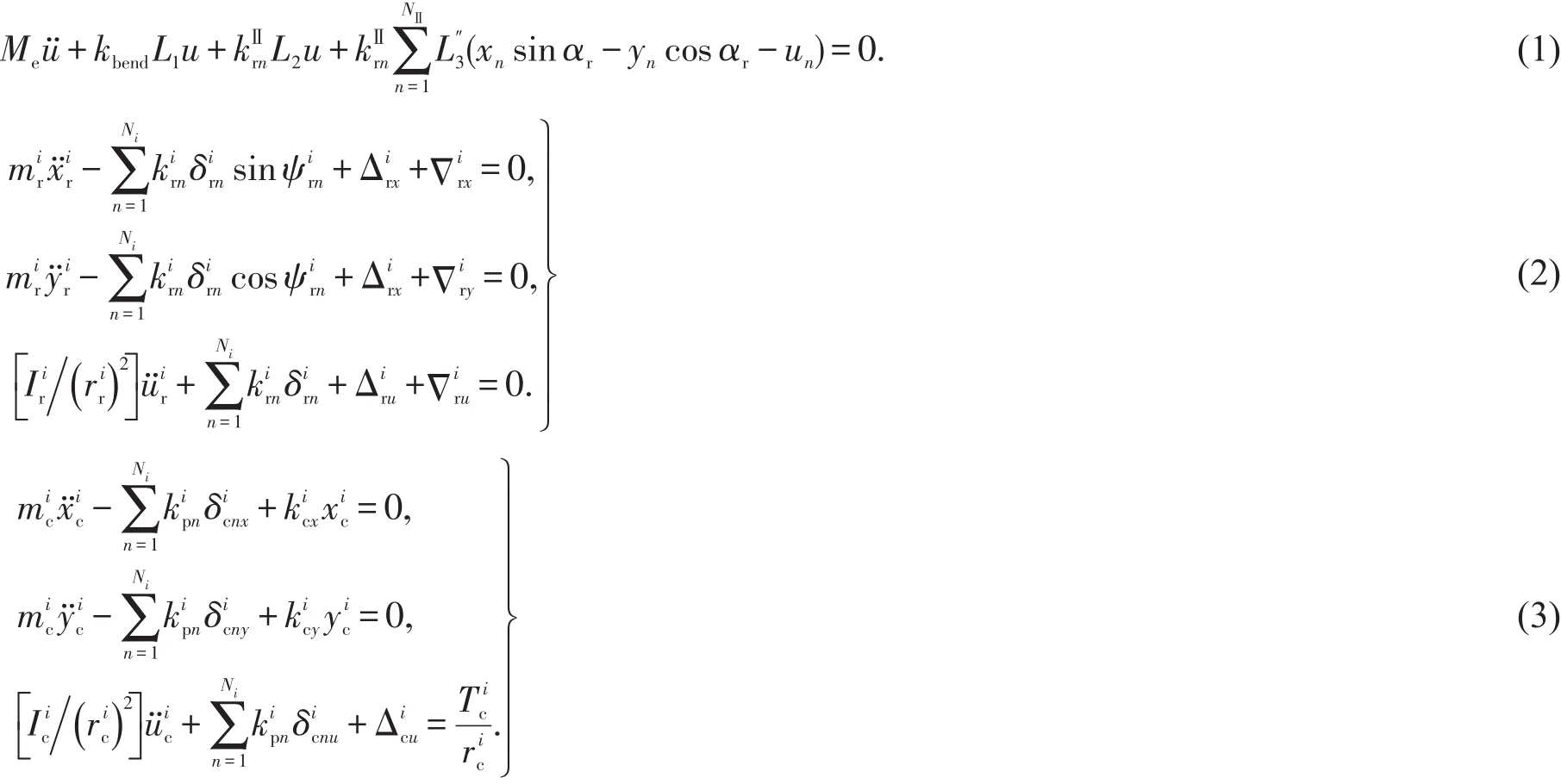
式中：Me表示第Ⅱ级内齿圈的等效质量；kbend=EI/R3(1-v2),E为第Ⅱ级内齿圈材料弹性模量，v为第Ⅱ级内齿圈材料泊松比，R为第Ⅱ级内齿圈的中性层半径，I为第Ⅱ级内齿圈的截面惯性矩；L1,L2和L3为无量纲算子（详见文献[15-17]）分别为第i级构件h的质量和转动惯量；分别为第i级太阳轮、内齿圈与行星轮的啮合刚度；分别为第i级太阳轮、内齿圈与行星轮沿其啮合线的微位移；为第i级行星架相对行星轮的位移沿行星架j方向的投影；为第i级构件h的支承刚度和扭转刚度；krus,krbs分别为第Ⅱ级内齿圈单位长度上的切向与径向刚度；为行星轮支承刚度；为第i级构件h所受的外力矩；表示第i级内齿圈、行星轮在j方向上的弹性耦合项；表示第i级内齿圈在j方向上的支承耦合项表示第i级构件h的扭转耦合项.弹性支承薄壁内齿圈两级行星传动系统各级基本参数及其余符号意义可参考文献[15-17].

2 弹性支承薄壁内齿圈两级行星传动系统齿轮副时变啮合刚度

第i级第n个行星轮内外时变啮合刚度可写成啮合刚度均值与其变动量之和的形式

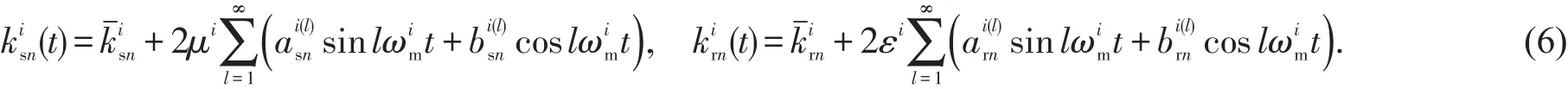
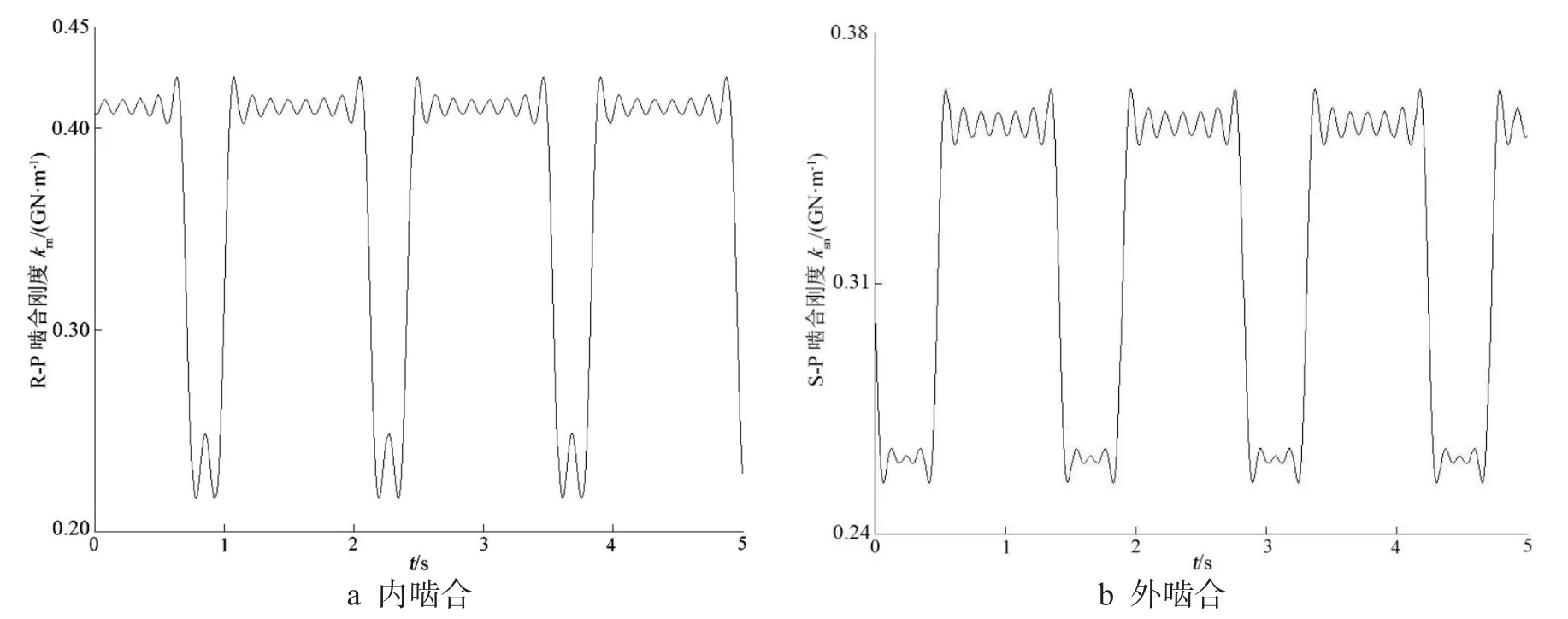
图2 第Ⅰ级行星传动内外时变啮合刚度[15-16]

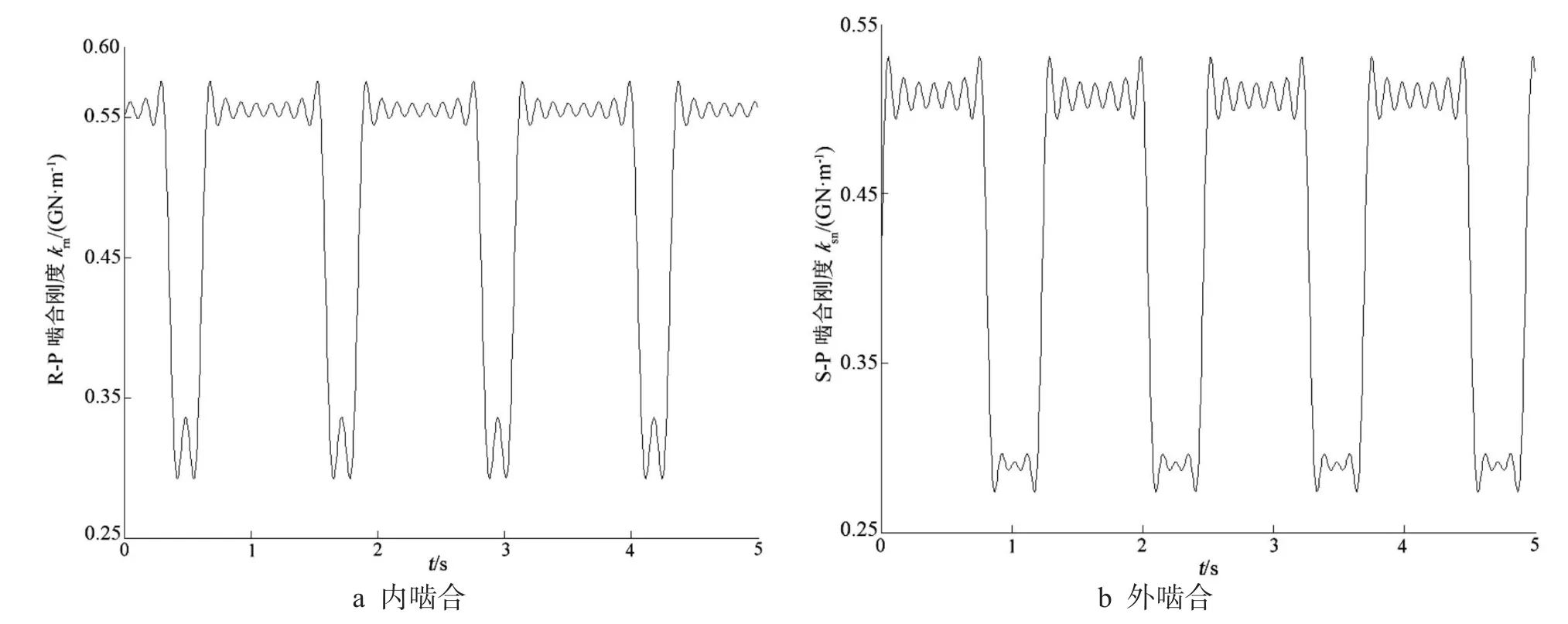
图3 第Ⅱ级行星传动内外时变啮合刚度[15-16]

3 级间耦合刚度变化对两级行星传动系统啮合动载荷的影响

3.1 级间耦合刚度变化对啮合动载荷的影响

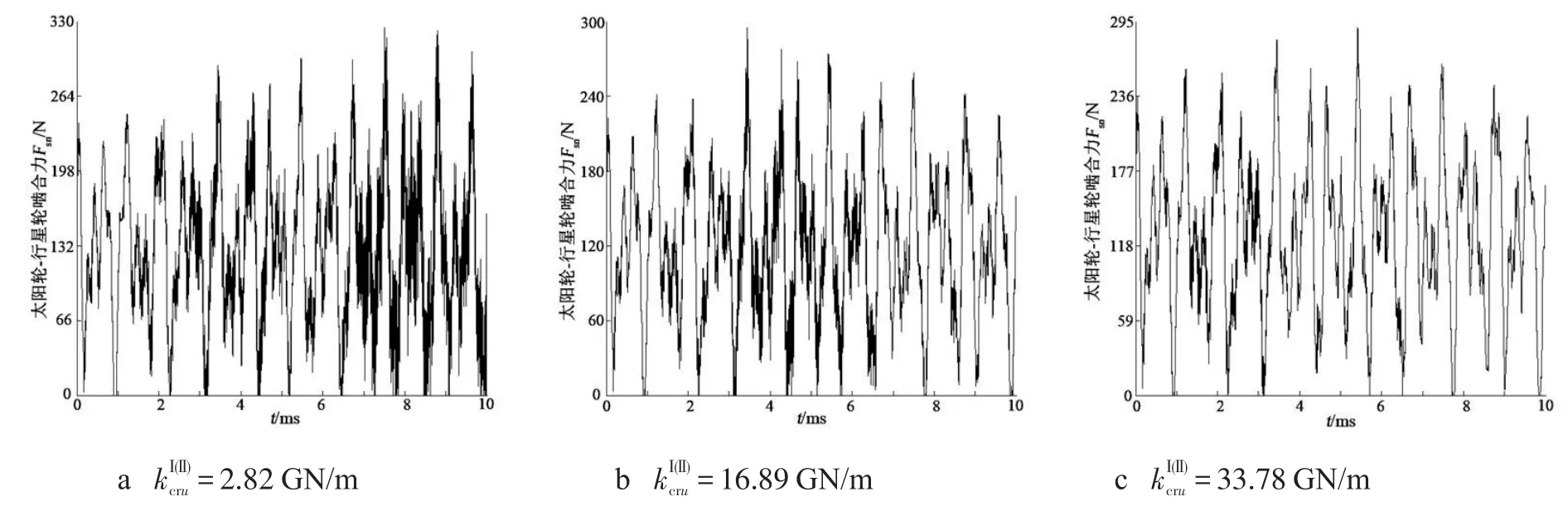
图4 级间耦合刚度对第Ⅰ级太阳轮-行星轮啮合动载荷的影响

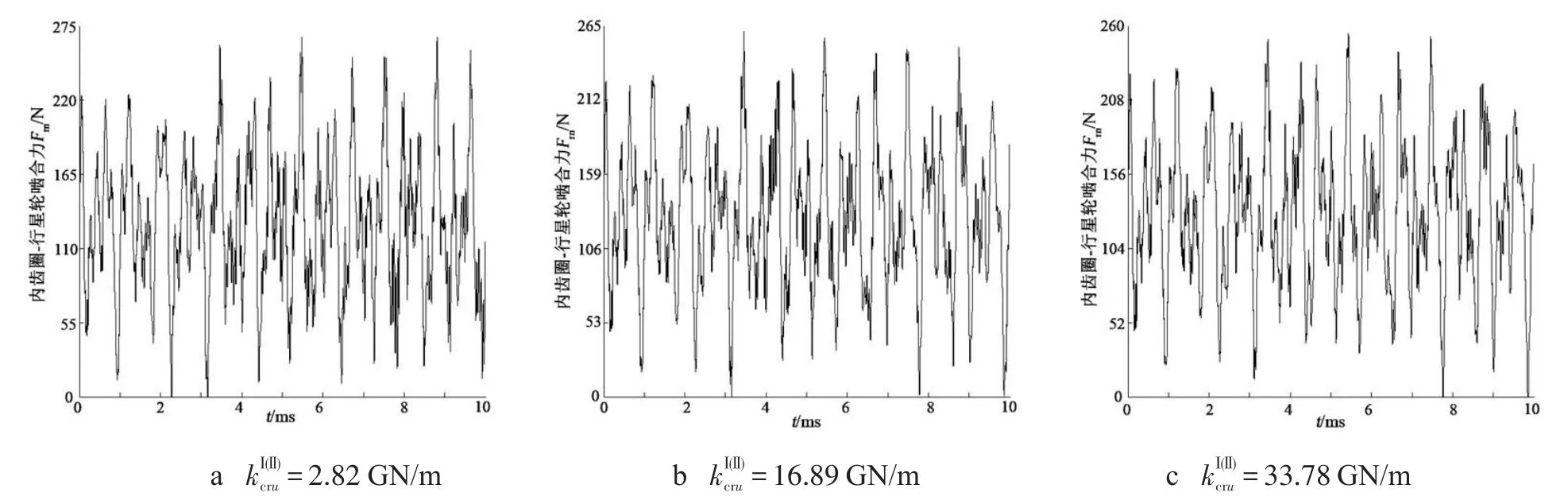
图5 级间耦合刚度对第Ⅰ级内齿圈-行星轮啮合动载荷的影响

图6 级间耦合刚度对第Ⅱ级太阳轮-行星轮啮合动载荷的影响

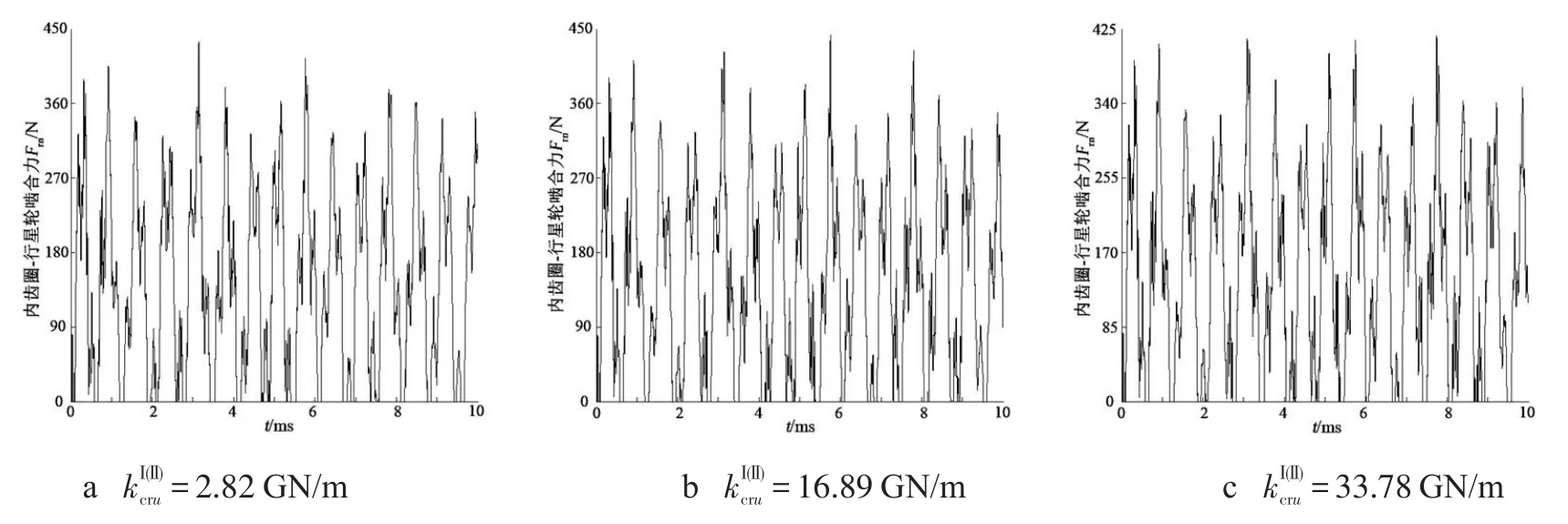
图7 级间耦合刚度对第Ⅱ级内齿圈-行星轮啮合动载荷的影响

从图4可以看出，随着第Ⅰ级内齿圈与第Ⅱ级行星架间耦合刚度的增大，第Ⅰ级太阳轮与行星轮间的啮合动载荷减小，且发生了脱齿现象，此时它们处于单边冲击状态，齿面处于脱离啮合状态的时间逐渐缩短.从图5可以看出，随着第Ⅰ级内齿圈与第Ⅱ级行星架间耦合刚度的增大，第Ⅰ级内齿圈与行星轮间的啮合动载荷减小，且它们间发生了单边冲击脱齿现象，这种脱离啮合状态的时间较短.从图6可以看出，随着第Ⅰ级内齿圈与第Ⅱ级行星架间耦合刚度的增大，第Ⅱ级太阳轮与行星轮间的啮合动载荷减小，比较图4和图6可以发现，它们相较于第Ⅰ级太阳轮与行星轮间的啮合动载荷有所减小，且啮合动载荷波动平稳，但发生了较严重的双边冲击脱齿现象.从图7可以看出，随着第Ⅰ级内齿圈与第Ⅱ级行星架间耦合刚度的增大，第Ⅱ级内齿圈与行星轮间的啮合动载荷先保持不变后减小，发生轮齿脱齿现象，且处于双边冲击状态.

3.2 级间耦合刚度 变化对啮合动载荷的影响

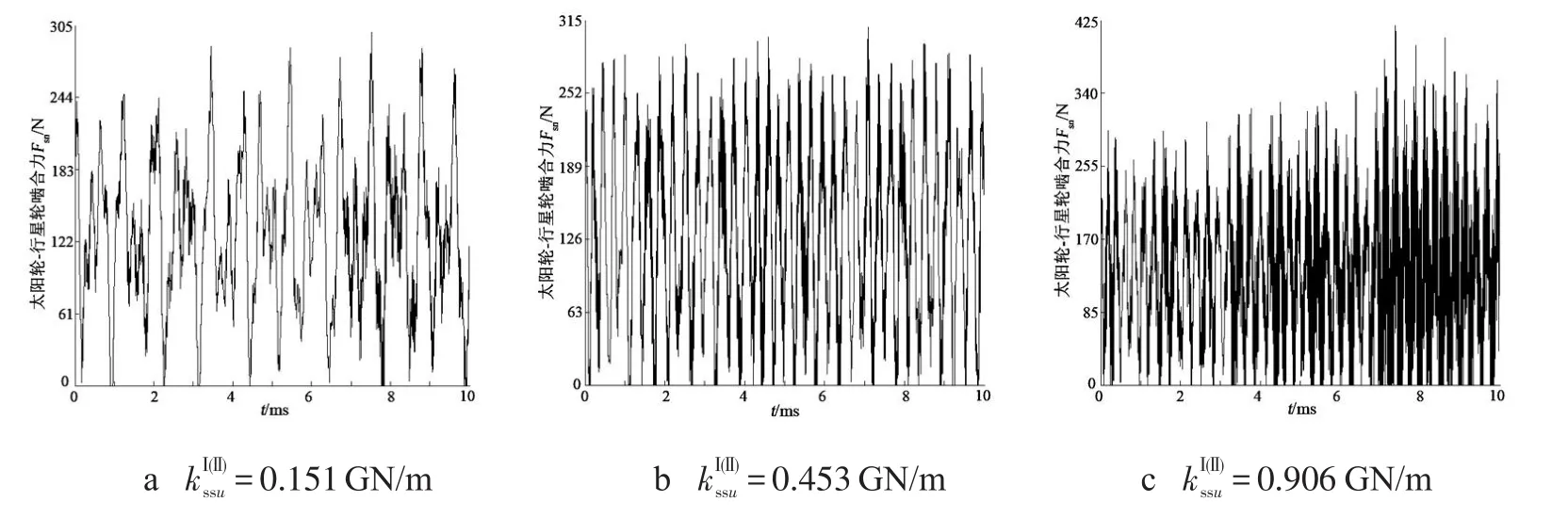
图8 级间耦合刚度 对第Ⅰ级太阳轮-行星轮啮合动载荷的影响

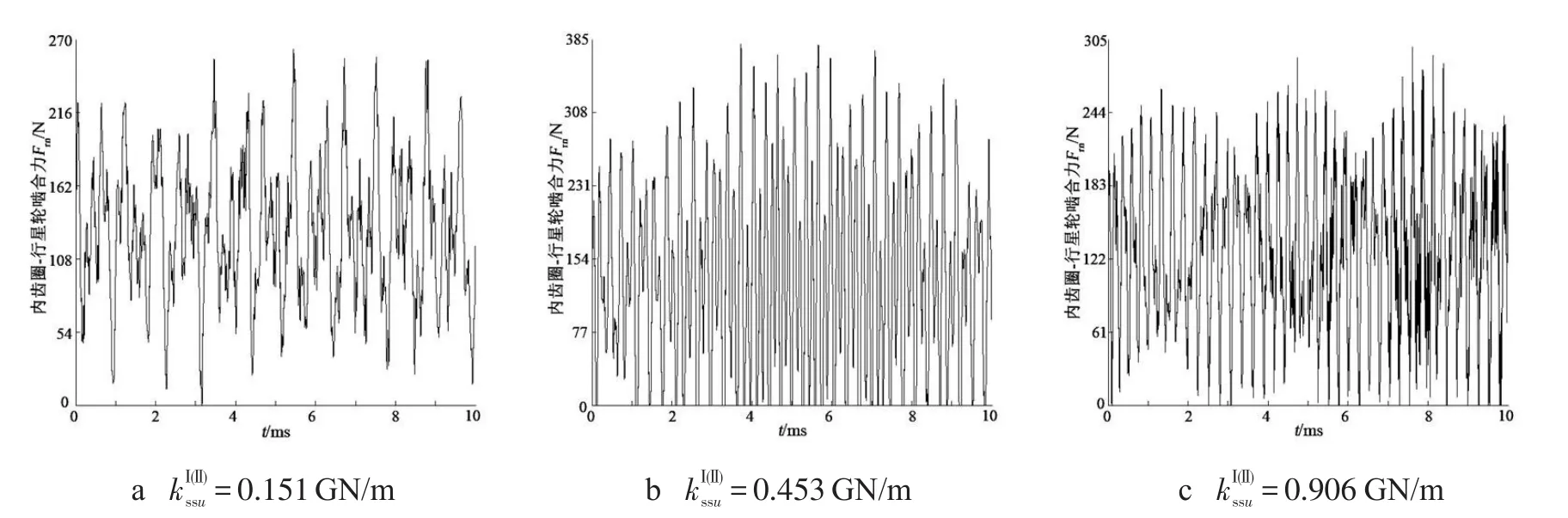
图9 级间耦合刚度 对第Ⅰ级内齿圈-行星轮啮合动载荷的影响

图10 级间耦合刚度对第Ⅱ级太阳轮-行星轮啮合动载荷的影响

图11 级间耦合刚度对第Ⅱ级内齿圈-行星轮啮合动载荷的影响

从图8可以看出，随着第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度的增大，第Ⅰ级太阳轮与行星轮间的啮合动载荷增大，其增幅较大；从图8还可以发现，随着第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度的增大，第Ⅰ级太阳轮与行星轮间从单边向双边冲击状态转变，且这种脱离啮合状态的时间延长.从图9可以看出，随着第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度的增大，第Ⅰ级内齿圈与行星轮间的啮合动载荷先增大后减小，其增、减幅均较大.从图9还可以发现，随着第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度的增大，第Ⅰ级内齿圈与行星轮间从单边向双边再到单边冲击状态转变，且脱齿啮合状态的时间在延长后有所缩短.从图10可以看出，随着第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度的增大，第Ⅱ级太阳轮与行星轮间的啮合动载荷先减小后增大，减、增幅均不大，它们间发生了双边冲击脱齿现象，且波动平稳性逐渐变差.从图11可以看出，随着第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度的增大，第Ⅱ级内齿圈与行星轮间的啮合动载荷减小，其减幅较大，第Ⅱ级内齿圈与行星轮间从双边向单边冲击状态转变，且齿面处于脱离啮合状态的时间缩短.

4 结论

考虑第Ⅱ级行星传动内齿圈弹性变形和弹性基的约束，通过级间耦合的方法建立了某混合动力系统中的两级行星齿轮机构在弹性支承下的刚柔耦合混合动力学模型，基于所建立的模型，采用Runge-Kutta法求解了传动系统的动力学微分方程，研究了级间耦合刚度变化对传动系统啮合动态载荷的影响，研究结果表明：

（1）随着第Ⅰ级内齿圈与第Ⅱ级行星架间耦合刚度的增大，在一定程度上降低了第Ⅱ级太阳轮、内齿圈与行星齿轮间的啮合动载荷；第Ⅰ级太阳轮与行星轮间的啮合动载荷波动次数有所减小，但第Ⅰ级内齿圈与行星轮和第Ⅱ级行星传动各齿轮副间的啮合动载荷波动次数几乎不变，且第Ⅰ级内齿圈与第Ⅱ级行星架间耦合刚度不仅对第Ⅰ级行星传动各齿轮副间的啮合动载荷产生影响，还对第Ⅱ级行星传动各齿轮副间的啮合动载荷产生了影响.

（2）随着第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度的增大，较大幅度地降低了第Ⅱ级内齿圈与行星轮间的啮合动载荷，第Ⅰ级和第Ⅱ级行星传动各齿轮副间的啮合动载荷波动影响较复杂，且第Ⅰ级太阳轮与第Ⅱ级太阳轮间耦合刚度不仅对第Ⅰ级行星传动各齿轮副的啮合动载荷产生影响，还对第Ⅱ级行星传动各齿轮副的啮合动载荷产生影响.