关于Ducci序列的周期性

周方敏

（肇庆学院 数学与统计学院，广东 肇庆 526061）

1 概论

设 v=(a0,a1,…,an-1)∈Zn,定义 Zn上的Ducci映射为

称序列

为Ducci序列,Ducci序列也叫n-数游戏.1800年,Ducci E首先研究了此映射.Ducci映射是一种差分方程,它与非线性动力系统、混沌理论及数值分析都有关系[1-2].文献[3]研究了Ducci映射与实数的连分数的表示之间的关系.文献[4]列举了一些有关Ducci序列的公开问题.

Ducci序列Dv中的元素最终会落到集合{0 ,1}n中去[5-6],因此它本质上是F2n中的序列.由于F2n是有限集,因此Dv是周期序列,其周期由初始向量v及其维数n唯一确定.文献[7]研究了Ducci序列的最大周期与有限维元胞自动机的最大周期的关系.由于历史原因,人们一直在研究如何用维数n来刻画Dv的周期[4,6,8].

第1个结论是:当n为2的方幂时,Dv的周期恒为1(即序列中只有有限个非零向量)[9-10].当维数固定时,对于不同的初始向量v,Dv的周期也不同.Dv的最大周期和周期分布也是人们热衷研究的对象.文献[11]给出了最大周期的一些整除性质及数值计算结果.文献[12]证明了,当整数k不是2的方幂时,一定存在以k为周期的Ducci序列.文献[13]指出:研究Dv的周期实际上是研究F2的某个扩域中的n次单位根在加1之后的乘法阶的变化情况.在现有文献中,研究Dv的周期的工具主要有2种:线性空间F2n上矩阵的最小多项式和定义于F2上的环中的元素的乘法.这2种工具各有优势,但本质上是等价的.

本文利用环中元素乘法研究Dv的周期,证明Dv的周期等于环中某个元素的乘法阶,并指出Dv的周期性质类似于有理数的p-adic展开式的周期性质.

设 v=(a0,a1,…,an-1)∈F2n,定义F2n上的Ducci映射

可以看出,以这种方式定义的F2n上的Ducci映射本质上与Zn上的Ducci映射等价.称序列

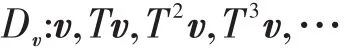
为F2n上的Ducci序列.定义

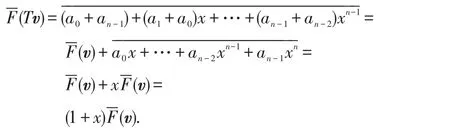
根据归纳法,有

根据映射F和的定义,能够将Ducci映射转化到环里元素的乘法,因此Ducci映射的周期性就转化到环里元素的周期性.

2 Ducci序列的周期性

定义1设v∈F2n,若存在自然数u和正整数e,使得Tuv=Tu+ev,则称e为Dv的周期;称满足Tuv=Tu+ev的最小自然数u为Dv的不循环长度.

下面给出本文的主要结论及其证明.

定理1设v∈F2n,且的最简分式是,gcd(b(x),1+x)=1,α≥0.则Dv的最小正周期是1+xmodb(x)的乘法阶,不循环长度为α.

证设1+xmodb(x)的乘法阶为e,则

在式(1)的两边同乘以 gcd(F(v),1+xn)(1+x)α,得

设k是Dv的1个周期,β是Dv的不循环长度,即Tβ+kv=Tβv,则

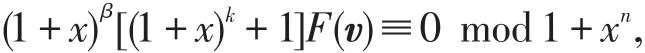
在上式中消去gcd(F(v),1+xn),可得

因为 gcd(a(x),(1+x)αb(x))=1,所以

得(1+x)β≡0 mod(1+x)α,这表示β≥α.所以Dv的不循环长度为α.

因为gcd(1+x,b(x))=1,式(2)表明(1+x)k≡1 modb(x).满足前式的最小正整数k是1+xmodb(x)的乘法阶.

注1 Ducci序列的周期性与有理数r=a/(pab)(这里gcd(a,pαb)=gcd(p,b)=1)的p进制展开式的周期性类似.r的p进制展开式的循环节长度是pmodb的乘法阶,r的不循环长度为α.r的循环节长度只被b确定,而r的循环节被a和b确定.

注2 根据有限域上的多项式理论,1+xmodb(x)的乘法阶等于多项式b(x+1)在环F2[x]/(1+xn)中的阶[14].

下面讨论最小正周期达最小值(周期为1)和最大值的Ducci序列.易知,Dv的周期为1当且仅当Dv中的序列最终都是零向量.

命题1设n=2km是正整数,m为奇数,且v∈F2n,则Dv的周期为1当且仅当是F(v)的因子.特别地,若n是2的方幂,则序列Dv的周期为1.

证Dv的周期为1,当且仅当存在整数i≥2k,使得Tiv是零向量;当且仅当当且仅当当且仅当因为

命题2设n=2km是正整数,m为奇数,且w=(1,0,…,0)∈F2n,则Dw是集合{Dv|v∈F2n}中具有最大的最小正周期的元素.

证这里所使用的符号同定理1.任取设xn+1=(x+1)2kg(x),则b(x)|g(x)且所以,g(x+1)的阶大于或者等于b(x+1)的阶,因此Dw最小正周期是最大的.

例1设n=2⋅32,xn+1=(1+x)2(1+x+x2)2(1+x3+x6)2=(1+x)2p(x)2q(x)2,ordp(1+x)=3,ordq(x+1)=63.

1)取w=(1,0,…,0),F(w)=1,ordp(x+1)2q(x+1)2=126,所以序列Dw的不循环长度为2,周期为126.