探索如何在高中数学教学中发散学生的思维

◆刘顺利

(山东泗水县第一中学)

所谓的发散思维又称为求异思维，是指在数学教学过程中，教师要有意识地给学生搭建思维发散的平台，使学生在知识灵活应用中，在求新、求异的过程中掌握知识，锻炼能力。那么，在新时期的高中数学教学过程中，我们该如何发散学生的数学思维呢？

一、一题多解活动

随着课改理念的贯彻落实，各个学校开始重视一题多解活动的开展，虽然是有助于学生数学思维的发散，有助于学生基本数学知识的灵活应用，但新的问题有重新出现，即多解并不是学生自己探索得到的，而是教师给出、讲出来的。可是，这样的一题多解活动只是丰富了学生的解题思路，让学生在死记硬背或者是根据答案理解的过程中形成多种思路，并不能真正让学生的数学思维得到发散。所以，在高中数学一题多解活动中，教师要充分发挥学生的课堂主体性，使学生在自主寻找多种解题思路中，自主对相关知识的解答中掌握知识，进而，为学生数学思维的发散做出贡献，提高效率。

例如，等比数列{an}的前n项和为Sn，已知对任意的n∈N*，点(n，Sn)均在函数y=bx+r(b>0且b≠1，b，r均为常数)的图像上。

(1)求r的值。

(2)当b=2时，记bn=2(log2an+1)(n∈N*)

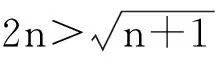
这是一道高考题，高考时我们不允许学生进行多种解答方式的尝试，但课下我们可以组织学生进行思考，深入挖掘自己大脑中的知识，寻找各个量之间的关系，以此来提出多种解答方法，并与小组之间进行讨论交流，以此来丰富学生的解题经验，同时，也能在多种解题思路的寻找中发散思维。所以，在该题的第(2)问的解答时，我们的学生就找到了将近10种的解答思路，其中有两种是我们在上课时常用的，也是学生在考试时出现最多的答案，即：第一种是通过假设法进行计算的，学生通过假设当n=k时结论成立，来证明当n=k+1时结论成立即可。第二种是寻找bn与3/2·5/4·…2n+1/2n之间的关系来进行证明。其余解题方法在此不在进行一一介绍，但从整个过程可以看出，学生积极地参与对高效数学课堂的实现，同时，也让学生在多种解题思路的寻找中发散思维。当然，除了一题多解之外，一题多变活动，也是有助于学生思维的发散的，学生在一类问题的自主对比中掌握知识，提高学习效率。

二、自主猜想活动

自主猜想是学生思维灵活的表现，也是提高学生解题效率，培养学生解题能力的有效活动之一。所以，在培养学生数学发散思维的过程中，教师要充分发挥学生的主动性，要鼓励学生大胆猜想，这样不仅能够有效的找到已知条件与未知条件之间的关系，也有助于提高学生的知识利用率。因此，在实际数学教学过程中，教师要鼓励学生进行探究猜想，以期能够真正使学生的数学思维得到发散。

还以上文中的例题为例，学生要想找到“bn与3/2·5/4·…2n+1/2n”之间的关系，除了依靠学生日常的解题经验之外，主要依靠的就是学生的自主探究和大胆猜想，即在求解第一问r的值时，我们已经求出：

bn=2n，详细的解题过程略，而bn与3/2·5/4·…2n+1/2n之间的关系则是，3/2·5/4·…2n+1/2n=b1+1/b1·b2+1/b2·…·bn+1/bn这样的关系的找到则成为了解决本题的关键。所以，我们也可以看到，学生大胆的猜想是有助于学生思维的发散的，对学生基本数学知识利用率的提高也起着非常重要的作用。

三、分析探究活动

在批改试卷的时候，我们常常会发现一些学生证明了一大片发现与所求结论没有关系，所以，整个都得划掉，然后重新找地方证明。这主要是因为学生在分析已知条件的时候没有把握好，或者说是找到已知与未知之间的关系，但没有找到已知与所求未知之间的关系，两者是有区别的。所以，在实际教学过程中，我们可以通过试题的分析探究来逐渐发现学生的数学思维，使学生在思考探究中形成能力。

还以上文的例题为例，以第一问求r的值为例，在解题时，教师要引导学生分析题干，找到相关量之间的关系，即通过对“任意的n∈N*，点(n，Sn)均在函数y=bx+r(b>0且b≠1，b，r均为常数)的图像上”这一条件的分析，找到Sn的表达式，即Sn=bn+r，这就是解答第一问的关键。而这一分析探究的过程，或者说是找关系的过程也对学生数学思维的发散，对学生灵活的搭建知识点之间的联系有着十分紧密的关系。

总之，在高中数学教学过程中，教师要充分发挥学生的课堂主体性，要通过恰当活动的组织来发散学生的数学思维，使学生在知识灵活应用中形成基本的数学素养。