基于离散元法的集料针片状含量对行车振动噪声的影响
2018-10-17刘力源
刘力源, 陈 长, 张 翛
(1.山西省交通科学研究院 黄土地区公路建设与养护技术交通行业重点实验室, 山西 太原 030006;2.同济大学 道路与交通工程教育部重点实验室, 上海 201804)
随着交通量的急剧增长,城市的交通噪声问题日益严重,NCHRP(National Cooperative Highway Research Program)的研究表明[1]:机动车的行车噪声在交通噪声污染中占有很大比例.从产生机理来看,行车噪声包含振动噪声和气动噪声两类.对于城市而言,由于交通拥挤、车辆行驶速度较低,导致振动噪声所占的比例较大.因此,降低行车振动噪声对于改善城市交通声环境有重要的意义.
路表特征技术委员会(PIARC)定义了4种不同的路面构造波长:微观纹理(<0.5 mm),宏观纹理(0.5~50 mm),粗大纹理(50~500 mm),路面平整度(0.5~50 m).ISO(International Standards Organization)对上述4类不同波长路表纹理进行研究,发现宏观纹理和粗大纹理对路面行车噪声有重要影响.对于沥青路面,集料形态会影响路表宏观纹理和粗大纹理,因此也会影响行车噪声.目前从集料形态这个层面去探讨其与行车噪声影响关系的研究很少,很多研究都是从更宏观的路面构造波长进行研究,比如路面平整度,并得到有意义的结论[2]:平整度对行车噪声有显著影响,随着平整度的增大,行车噪声呈增大的趋势.然而,从更细观的层面上来看,集料形态会对行车噪声造成怎样的影响还没有比较具体的研究.
在道路工程中,集料形态可分为针片状和规则状两种,通常使用针片状颗粒含量反映整体的集料形态特征.针片状颗粒含量不仅会影响集料的施工和易性,而且会影响混凝土的强度.为了研究集料形态对行车振动噪声的影响,本文通过针片状颗粒含量这一指标,研究其与行车振动噪声的关系.由于本文的研究比较细观,传统试验基于以下原因难度较大:首先,集料形态特征需要人工观测,很难准确控制针片状颗粒含量;其次,需要成型大量的路面试件或者铺筑试验路,从而导致了工程量过大.因此,本文利用数值模拟的方法进行研究.随着计算机技术的发展,离散元方法在道路工程中得到越来越多的应用.目前,离散元在沥青路面中的模拟仿真主要体现在[3-7]:集料形态、均匀性等对沥青混合料力学性能的影响;车辆荷载作用下沥青混合料微观力学响应;沥青混合料断裂的微观力学机理等方面.尚没有研究将该方法应用于道路噪声领域.本文采用离散元方法,通过控制针片状颗粒含量,利用离散元软件成型不同的沥青路面模型,模拟车轮在路表的运行过程,来分析针片状颗粒含量对行车振动噪声的影响.
1 行车振动噪声的评价方法
离散元是一种数值模拟方法,无法直接模拟和计算行车振动噪声,因此,首先需要提出可以表征行车振动噪声的方法.
国外研究发现[8]:轮胎-路面之间的接触状态对行车振动噪声有很大的影响,尤其对于车轮与路面的接触压力而言,它与行车振动噪声之间应该存在某种联系,但这二者之间具体的关系尚不清楚.设想路面是光滑且平整的,那么当车轮在路面上匀速直线滚动时,车轮与路面之间的竖向接触压力是恒定的.由于实际路面的路表颗粒性很强,当车轮碰撞到较大的集料颗粒时,车轮与集料之间会产生径向的撞击力,该径向力引起了二者的振动作用,从而形成振动能,并以声波的形式向四周辐射形成振动噪声.该径向撞击力是行车振动噪声的激励源,同时也引起轮地接触压力发生变化,导致轮地接触压力的波动性变强.由此可以看出,行车振动噪声与轮地接触压力的波动性有关,接触压力的波动性越大,振动噪声越大.
基于这一分析,本研究采用理论分析、现场试验和模拟计算做进一步论证.现场试验选取一段高噪声沥青路面和一段普通沥青路面进行现场噪声测试;模拟计算将利用离散元软件建立这两种路面模型,计算车轮与路面之间的接触压力;最后对现场试验结果和模拟计算结果进行对比分析.
1.1 理论分析
根据研究方法,声学分为波动声学、射线声学和能量声学.波动声学是使用微粒模型来描述波传播,它是进行声学各学科研究的最基本和最重要的方法,因此,本文借助波动声学对行车振动噪声与轮地接触压力之间的关系进行理论分析.
在进行分析之前需要引入一个声学概念:单极子源[9].单极子源是单个的球面形声源,它辐射的声波是离开源的径向距离r的函数.本文将行车时胎面与集料之间每次撞击所产生振动噪声的声源视作单极子源.
单极子源的声波动方程为
(1)
式中:p为声压;c为声速;t为时间.
方程(1)的通解为
rp=f1(ct-r)+f2(ct+r)
(2)
式中:f1代表向单极子源球外传播的部分;f2代表向球心反射的部分.假设球表面作简谐振动,向外传播的波为
(3)
式中:A为常数,由单极子表面给定的边界条件确定;ω为角频率;k为波数;φ为初相位.
单极子源的动量方程为
(4)
式中:ρ0是空气静态密度;u是质点速度.将式(3)代入式(4)可得质点速度为
(5)
在距离单极子源较远处质点速度与声压同相,并且满足方程(6)是声压与质点速度的关系式.
ρ0c
(6)
汽车在行驶过程中,当车轮碰撞到较大的集料颗粒时,在轮胎与路面接触的前沿区,存在一个接触点A,如图1所示.在A点,轮胎在垂直方向的分速度瞬间变为零,轮胎的矢量速度由v0突变成水平速度v1,二者的数值是相等的.根据矢量合成法则,在A点还存在指向胎中心区域的矢量速度v2,以及因速度突然改变而生成的加速度.该加速度是由一个在A点指向轮胎中心区域的径向力F引起的.因而轮胎与路面之间的接触压力会产生变化,这种变化由胎面与集料之间突然增大的径向撞击力引起.

图1 车轮与路面接触示意图
将车轮与路面集料接触的花纹块视作弹性体,设弹性系数为K,质量为mb,将胎面与地面之间的振动简化为简谐振动,变形量为ξ,角频率为ω.根据振动理论可知
F=Kξ
(7)

(8)

(9)
式中:x0为简谐振动时间参量.根据质点速度与声压的关系式(6)可得
(10)
式(7)~(10)联立可得到行车振动噪声声压的表达式
(11)
式中:mb与K均为常数,F由胎面与集料间的撞击产生,p与F之间存在正相关关系.同时,轮胎胎面与集料之间撞击力F也引起轮地接触压力发生突变,导致轮地接触压力的波动性变强.由此可见,行车振动噪声的声压大小与车路接触压力的波动性有关联,接触压力的波动性越大,声压越大.
1.2 现场试验
振动噪声只是行车噪声中的一部分,单独获取其噪声值十分困难.对于车内的驾驶员或乘客而言,当车内环境处于完全封闭状态时,车内噪声基本上由车体振动产生,因此,本研究将车内噪声视作行车振动噪声.
分别在微表处路段和上面层级配为SMA-10(沥青玛蹄脂碎石最大公称粒径为10 mm)的路段各选取10个测点进行车内噪声测试,采用HS5618A型积分声级计,参照滑行法测试车内噪声.试验过程中车辆门窗保持关闭状态,保证车内环境是一个封闭的空间,同时测量人员手持声级计坐在副驾驶位置.分两次测量,第1次车速控制在80 km·h-1,第2次车速控制在40 km·h-1.图2是桩号NX302处的试验现场.

图2 试验现场
删除每个路段内车内噪声的最大值和最小值,将测量结果汇总,如图3所示.
由图3可知,在80 km·h-1和40 km·h-1车速下,微表处路段的车内噪声均要明显高于SMA-10路段的车内噪声.因此,在同一车速状态下,微表处路面的行车振动噪声要高于SMA-10路面的行车振动噪声,这与微表处是一种高噪声路面的实际情况吻合.

a 80 km·h-1

b 40 km·h-1
1.3 模拟计算
采用的仿真软件是离散元颗粒流软件PFC3D.PFC3D能够模拟球体颗粒间的相互运动与相互作用,它还可以将任一颗粒与其临近的颗粒组合成大小不限、形状随意的组合体来模拟块体结构问题.应用于道路工程中,该软件可以模拟形态各异的集料、沥青混合料试件等,并可以进行力学分析.本文利用PFC3D分别构建微表处路面和SMA-10路面,并且建立车轮模型,模拟在40 km·h-1和80 km·h-1车速下车轮在路面上的滚动过程,然后计算竖直方向车轮和路面之间的接触压力.
选用直径为15 mm左右的小球单元,将其黏合成宽50 mm、外径200 mm的圆环块体模拟车轮,如图5所示.
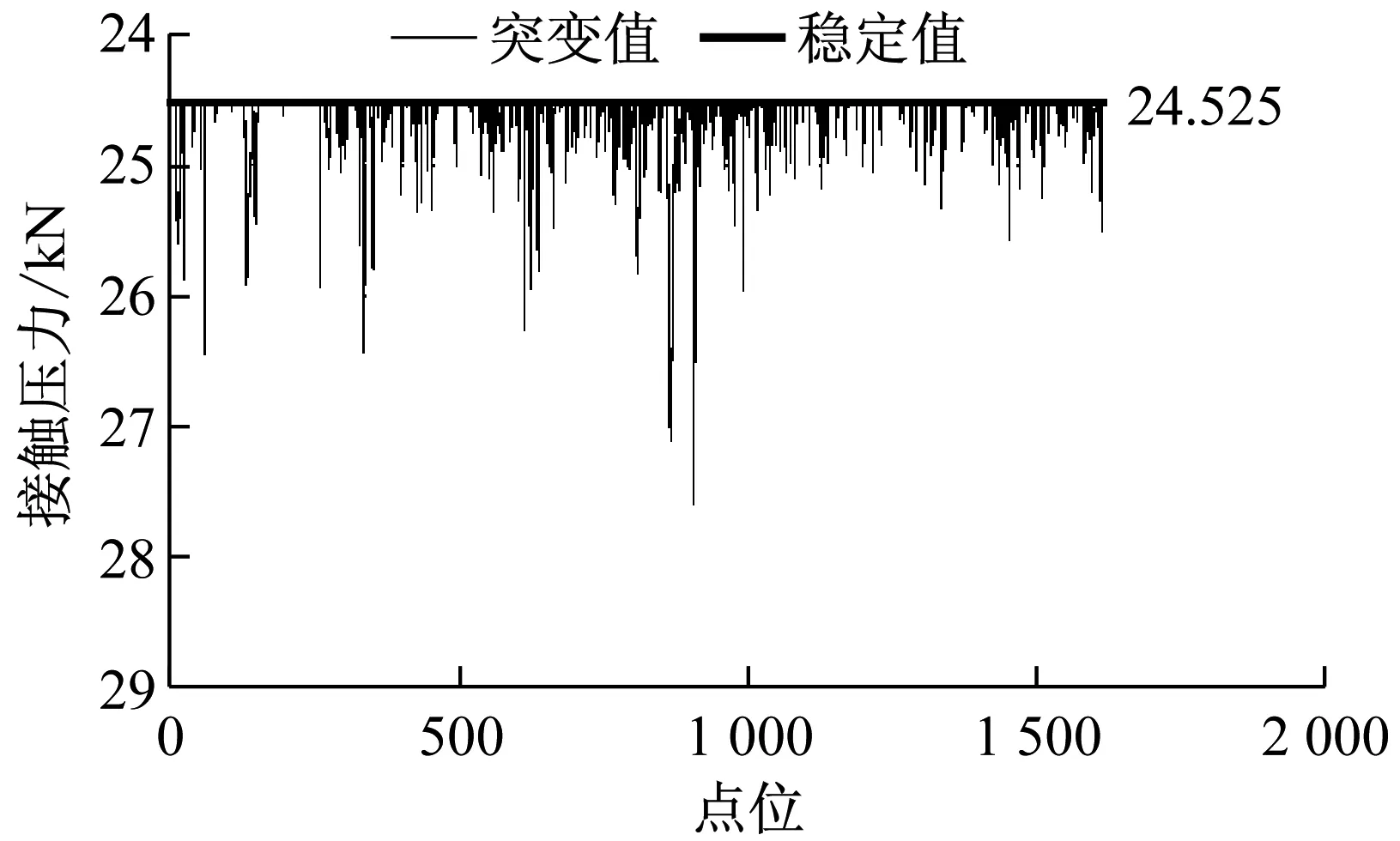
路面模型和车轮模型建立完成后,模拟车轮在路面上的行驶过程.路面模型的长边方向设置为y轴方向,车轮的竖直受力方向为z轴方向.首先,设置车轮沿路面行驶时的起始位置startpos和终止位置endpos.给车轮y向速度和旋转角速度,使车轮沿着y轴方向从startpos运行到endpos,保存轮地之间的竖向接触压力,并绘制波动图,如图6和图7所示.

表1 模型生成的级配

图4 微表处模型
由图6、7可知,在80 km·h-1和40 km·h-1的车速下,微表处路面的轮地接触压力的波动性均要明显强于SMA-10路面.结合理论分析与现场试验的结果可以得出:轮地接触压力的波动性越大,行车振动噪声也越大.根据这一关系,就可以利用轮地接触压力评价行车振动噪声.v

图5车轮模型
Fig.5Vehiclewheelmodel
2 建立模型
利用PFC3D软件建立不同针片状颗粒含量的沥青路面模型,模型采用AC-13(最大公称粒径为13 mm的细粒式沥青混凝土)的级配.我国现行规范规定:高速公路及一级公路的表面层,针片状颗粒含量不大于15%,其他等级公路的针片状颗粒含量不大于20%.因此,为了进行对比分析,构建4种沥青路面模型,其针片状颗粒含量分别为0、10%、15%和20%.

a 微表处路面
b SMA-10路面
Fig.6Volatilityanalysisoftire-roadcontactpressure(80km·h-1)

a 微表处路面

b SMA-10路面
Fig.7Volatilityanalysisoftire-roadcontactpressure(40km·h-1)
2.1 规则状和针片状集料生成
利用MATLAB软件实现随机形状的针片状颗粒和规则状颗粒.两种集料的形状控制方法相同,以规则状集料为例进行详细阐述:首先在一个单位立方体空间内生成N个随机点,形成点云.本文设置N=20,使用MATLAB的随机数产生函数得到20个随机点,如图8所示.

图8 随机生成点云
基于生成的点云,计算这些点所围成的凸包,得到不规则的凸多面体.MATLAB提供了函数F=convhulln(X)可以用来计算凸包,调用这个函数就可以筛选出组成多面体外表面的点,最终得到有n个顶点的任意多面体.对于规则状集料,将其长宽高的比例设定为1∶1∶1.由于生成的多面体不一定能满足集料的粒径要求,因此要首先得到生成多面体的最小包围盒,对该包围盒沿着3个方向进行拉伸或压缩得到立方体的包围盒,如图9所示.

图9 规则状集料的多面体壳
图中的灰色多面体就是随机形状的规则状集料的多面体壳,粗实线包围的立方体就是它的最小包围盒,如果集料的粒径为16 mm,可以将最小包围盒的边长设定为16 mm.根据文献[11]中的用球体填充多面体壳的算法,得到了粗集料模型,如图10所示.

图10 规则状集料模型
日本和欧洲对针片状颗粒的定义是最长端与最薄部分的比例L/b为3∶1,而美国材料与试验协会(ASTM)规定了L/b为2∶1、3∶1和5∶1不同标准针片状颗粒含量的试验方法.SHRP(Strategic Highway Research Program)的SU-PERPAVEE仅规定5∶1一个标准.NCAT(National Center for Asphalt Technology)认为按照5∶1的规定,针片状含量的检测结果几乎为零,没有实际意义,建议采用3∶1.我国的《公路工程集料试验规程》采用3∶1定义针片状颗粒.因此,本文按照长∶宽∶高为3∶1∶1的比例生成随机形状的针片状集料模型,如图11所示.


图11 针片状集料模型
2.2 模型参数设定

在沥青路面的离散元模型中,需要添加粗集料、细集料和沥青3种元素.由于沥青混合料的复杂性,若使用PFC颗粒来详尽地模拟沥青胶浆的作用,则需要生成粒径极其小的球体颗粒,这对普通计算机来说在运算速度和内存大小方面是一个极大的挑战.同时考虑到车轮行驶时,其主要是与路表粗集料发生接触.因此,本文将沥青混合料颗粒按功能分为两类:一类是起骨架作用的粗集料,另一类是起黏结及填充作用的细集料.本文设定粒径大于等于2.36 mm的是粗集料,粒径小于2.36 mm的是细集料,粒径小于1.18 mm的颗粒忽略不计.同时,针对粗集料,要考虑形状要求,针对细集料,不考虑形状要求,用单元小球模拟.
在力学参数方面,粗集料内部接触单元以及粗集料之间的接触单元均采用线弹性接触模型.粗集料内部接触单元的法向接触刚度与切向接触刚度无穷大.粗集料单元之间的线弹性接触通过如下细观参数表征:两个clump单元接触处的法向刚度Kn;两个clump单元接触处的切向刚度Ks.Kn和Ks通过粗集料的抗压回弹模量E和泊松比ν来确定,计算公式如下:
Kn=2Et
(12)
Ks=2Gt
(13)
(14)
式(12)~(14)中:t为颗粒单元厚度,参考已有研究[13-14],将抗压回弹模量设定为55.5 GPa,泊松比设定为0.23.
采用平行黏结模型模拟沥青胶浆的作用.当采用平行黏结模型时,集料间用具有恒定法向刚度和切向刚度的一组弹簧作用在接触的区域内.对于平行黏结模型,需要确定的参数是平行黏结法向强度a和平行黏结切向强度b.参考已有研究[15],将a和b设定为50 kN.
粗细集料均采用相同的摩擦系数.文献[13]利用离散元模拟过不同摩擦系数下的贯入试验,研究发现:当摩擦系数从0.1增大到0.4时,相同贯入深度下的贯入阻力明显地增大,而当摩擦系数从0.3增大到0.5时,贯入曲线并没有发生明显差异.这说明具有较好纹理的集料颗粒比光滑集料具有更大的抵抗压缩荷载的能力,但是当纹理丰富到一定程度后,纹理的进一步增多对抵抗压缩荷载能力的提高没有明显作用.因此,设定粗细集料的摩擦系数为0.4.
车轮模型的尺寸参照车辙试验中试验轮的尺寸:直径200 mm,轮宽50 mm.目前常用小轿车的车重基本都在1.5 t左右,因此设定车轮质量为1 500 kg.
2.3 模型生成
根据2.2中所设定的参数,本节利用PFC3D生成不同针片状颗粒含量的路面模型.具体步骤为:
(1)按照50 mm×300 mm×50(1+s))mm的尺寸生成沥青路面模型的外围墙体,s是高度扩大系数,添加这一参数是为了方便后期的压缩成型.
(2)根据AC-13的级配填充颗粒,包括粒径大于等于2.36 mm的基球以及粒径小于2.36 mm的颗粒.根据针片状颗粒含量,用2.1中生成的针片状集料和规则状集料替换基球.
(3)压缩成型.
根据以上步骤,分别构建了针片状颗粒含量为0、10%、15%、20%的AC-13路面模型,如图12~15所示.

图12 针片状颗粒含量为0的AC-13路面模型

图13 针片状颗粒含量为10%的AC-13路面模型
路面模型构建完成之后,构建车轮模型,模拟车轮的滚动过程.
3 计算结果分析
考虑车速的影响,分别计算30、40、60和80 km·

图14 针片状颗粒含量为15%的AC-13路面模型

图15 针片状颗粒含量为20%的AC-13路面模型
h-1车速下的轮地接触压力.由第1节可知,轮地接触压力的波动性越大,行车振动噪声越大.为此本节提出振动系数这一指标表征接触压力波动的强弱程度,定义振动系数是突变值与稳定值偏差平方的和与发生突变的点位数比值的平方根,计算公式如下:
(15)
式中:M是振动系数;F突变是接触压力的突变值;F稳定是接触压力的稳定值;n是发生突变的点位数.根据式(15)计算4种路面在不同车速下的轮地接触压力的振动系数,结果如图16所示.

图16 振动系数的计算结果
由图16可知,随着车速的提高,振动系数呈增大的趋势,即车路接触压力的波动也变得更为剧烈.
当车速为30、40和80 km·h-1时,针片状颗粒含量为20%的路面的振动系数要明显高于其他3种路面.当车速为60 km·h-1时,针片状颗粒含量为20%的路面的振动系数略低于针片状颗粒含量为15%的路面,但要高于另外两种路面.总体而言,与其他3种路面类型相比,针片状颗粒含量为20%的路面,在4种车速状态下,其振动系数均处于较高的水平,因此其行车振动噪声也较高.
当针片状颗粒含量为0,10%和15%时,3条折线之间相互交叉,说明针片状颗粒含量较低时,振动系数与针片状颗粒含量的相关性不强;同时可以发现,随着车速的增大,不同针片状颗粒含量的路面,其振动系数的差值也在逐渐变小.这说明,当行车速度较高时,针片状颗粒含量对行车振动噪声的影响会变小.
假设有两种集料形态A和B,如图17所示.A集料凸起高度Δh大,沿路表长度Δl小;B集料凸起高度Δh小,沿路表长度Δl大.将车轮在A处的受力和在B处的受力简化至同一点进行分析.车轮受到牵引力、集料的撞击力和摩擦力3种力.图中,F牵引表示牵引力,FA和FB分别表示集料A和B的撞击力,fA和fB分别表示集料A和B的摩擦力.当Δh/Δl较大时,牵引力和撞击力之间的夹角较小,根据平行四边形法则,很显然,在车轮牵引力相同的情况下,和B相比,A对车轮的径向撞击力更大.由此可以分析本文的结论,当针片状颗粒含量过高时,影响了施工时的摊铺压实,导致路表颗粒参差不齐,集料凸起高度Δh较大,车轮与集料间的撞击力变大,造成了轮地接触压力的波动性变强,行车振动噪声变大.

图17 集料对车轮的撞击力分析
Fig.17Forceanalysisofcontactpointbetweenwheelandaggregate
4 结论
本文首先通过理论分析、现场噪声测试和离散元模拟计算,论证了行车振动噪声与轮地接触压力的关系,然后采用离散元颗粒流软件PFC3D构建了4种不同针片状颗粒含量的沥青路面模型以及车轮模型,分别模拟车轮在不同车速下在这4种路面上的运动过程,并计算轮地接触压力,分析其波动性,进而评价行车振动噪声,最终得出以下结论:
(1)建立轮地接触压力与行车振动噪声的关系.轮地接触压力的波动性越强,行车振动噪声越大.提出了通过轮地接触压力的波动性评价行车振动噪声的方法.
(2)当针片状颗粒含量为0、5%、15%时,针片状颗粒含量与行车振动噪声之间没有显著的相关性,但是当针片状颗粒含量为20%时,其行车振动噪声要高于低针片状颗粒含量的路面.而且,当车速增大,针片状颗粒含量对行车振动噪声的影响会变小.
(3)我国现行的规范规定:高速公路及一级公路的表面层,针片状颗粒含量不大于15%,其他等级公路的针片状颗粒含量不大于20%.通过本文的研究可知,这一规定在道路降噪方面也有实际的意义.当针片状颗粒含量超出规范的规定值后,不仅影响集料的施工和易性、降低混凝土强度等,还会造成较高的行车振动噪声,结论可以为低噪路面设计提供参考.
由于现场试验的操作难度较大,本研究采集到的现场实测数据较少,主要依靠离散元方法进行模拟仿真,对模拟结果尚缺乏进一步的验证,因此,下一步的研究需要结合一些现场试验对本文的结论做进一步的验证.
