三维立体测度视角下动态综合评价集结模型的比较

李望晨，王培承，王在翔，张利平

（潍坊医学院“健康山东”重大社会风险预测与治理协同创新中心，山东 潍坊 261053）

0 引言

经济或卫生领域管理工作中常见多指标综合评价问题，从某个固定时刻点按照指标体系将所有对象从指标集和对象集两个维度采集横截面测量信息，通过选择合适集结算法来设计模型，所有对象在这个二维静态情景下将信息集结计算为某个“综合指标”，据此在所有对象之间进行相对比较、排序择优[1]。这类静态情景下卫生综合评价问题有广泛代表性[2]，例如固定某年度作为数据采集时刻点，不去考虑前后年度动态变化影响，只是采集所有科室横截面指标测量数据，由综合评价模型在所有科室之间相对比较医疗质量优劣。

如果评价者不仅要在某个时刻横向比较静态差异情况，还想兼顾在某段时间内纵向比较动态变化情况，于是提出了动态综合评价问题，即在二维横截面数表中继续扩展引入时间维度，以对象、指标和时刻点三个维度测量数据为基础，扩展为三维立体数表作为复杂动态综合评价问题。一般做法是以间隔周期逐个时刻作为采集点，固定时刻每个对象关于每个指标采集测量数据，将各时刻点横截面数表依序纵向排列组成立体数表。这类动态综合评价工作优点就是从纵横向立体视角反映某段时间内累积水平，充分利用各时刻点指标差异和前后时刻点之间指标变化信息。因此，若实际条件允许、时序资料可取，有必要从多个时刻点采集数据，兼顾横向差异或纵向变化信息，按特定目标设计动态评价问题有扩展意义。于是本文将四种经典方法作为理论基础，以立体测量数据表为依据改进设计动态综合评价模型，由医疗质量工作案例比较检验有效性，促进医疗卫生领域领域更复杂问题中交流应用。

1 理论方法

1.1 问题描述

假设m个评价对象A1,A2,…,Am，依次从时刻t1，t2，…，tN为截点，关于指标体系c1，c2，…，cn采集测量信息，赋予指标内涵权重ω1，ω2，…，ωn。假设第k个时刻tk、第i个对象Ai关于第j个指标cj依次确定测量值xij(tk)。第k个时刻tk、第i个对 象 Ai情 况下 所有指 标c1，c2，…，cn测量 值表 示为xi1(tk)，xi1(tk)，…，xin(tk)。第k个时刻tk、第j个指标cj情况下所有对象A1,A2,…,Am测量值表示为x1j(tk)，x2j(tk)，…，xmj(tk)。i=1，2，…，m；j=1，2，…，n；k=1，2，…，N。于是，所有时刻t1，t2，…，tN、所有对象 A1,A2,…,Am关于指标体系c1，c2，…，cn测量值形成三维立体数据表，见表1。

表1 三维立体测量数据形式

其中每个时刻点为对象和指标维度横截面数表，每个对象为指标和时间维度纵剖面数表。m=1时为1个对象、m＞1时为多个对象；n=1时为1个指标、n＞1时为多个指标；N=1时为1个时刻、N＞1时为多个时刻。m＞1、n＞1、N=1时为某时刻多个对象或m=1、n＞1、N＞1为某对象多个时刻，此类多指标综合评价问题应用多见。下面考虑m＞1、n＞1、N＞1时，在多个时刻多个对象立体数据视角下设计多指标动态综合评价模型。

1.2 模型流程

动态综合评价问题体现固定时刻点横向差异和一段时间纵向变化信息。思路一：“先按时间合成、再作静态评价”。所有对象指标测量数据按时间纵向合成静态面板测量数据，由经典方法直接设计模型。因其思路成熟、简便易行而不必论证。思路二：“先作静态评价、再按时间合成”。在每个时刻点将所有对象由经典方法设计集结模型，将评价值按时间纵向合成。本文以思路二为基本做法，按照固定时刻点，将线性加权、TOPSIS、灰色关联和VIKOR法在动态情景中改进设计模型并从横纵向两类信息获取评价值，按时间加权合成总评价值，据此相对比较或排序择优。经典方法原有的基础知识详见有关文献。

1.2.1 模型一：线性加权法

由于指标属性、方向、量纲或数量级往往不同，须作无量纲预处理。所有对象从所有时刻点选取指标最小最大值，然后将指标体系进行预处理。以下数学记号相互通用。

指标cj：从所有对象按全部时刻点取最小值、最大值

成本指标:

（1）从横向差异分析。Ai关于测量数据yij(tk)加权求和[3]：

（2）从纵向变化分析 。假 设 ΔAi=(Δyi1(tk)，Δyi2(tk)，…，Δyin(tk))，关于指标c1，c2，…，cn加权求和：

其中，时刻点tk指标增减量为Δyij(tk)=yij(tk)-yij(tk-1)，k=2，3，…，N,令 Δyij(t1)=0 。

根据yi(tk)、Δyij(tk)大小均可将A1,A2,…,Am相对比较。

合成时刻点tk评价值：

时间权重反映信息集结过程中时刻点之间重视程度，如果时刻点作用相同则等分权重。一般按照“厚今薄古”思想来赋权，重视近期时刻点作用，由远近顺序来增大权重。

本文不妨采用简化算法[4]:

由时刻点t1，t2，…，tN合成总评价值：

越大则越优。

1.2.2 模型二：TOPSIS法[5]

计算 Ai与 A+、A-之间距离：

计算Ai相对贴近度：

计算 Δ Ai与 ΔA+、ΔA-之间距离：

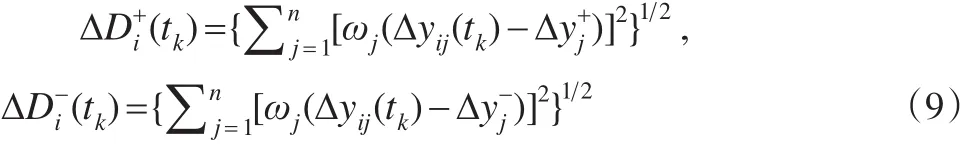
计算Ai相对贴近度：

根据Ci(tk)、ΔCi(tk)大小均可将A1,A2,…,Am相对比较。

合成时刻点tk评价值：

由时刻点t1，t2，…，tN合成总评价值:

越大则越优。

1.2.3 模型三：灰色关联法

（1）从横向差异分析。计算Ai与A+、A-之间灰色关联系数：

计算 Ai与 A+、A-之间关联度：

计算Ai相对贴近度：

（2）从纵向变化分析。计算ΔAi与ΔA+、ΔA-之间灰色关联系数：

计算 Δ Ai与 Δ A+、Δ A-关联度：

计算Ai相对贴近度：

根据Ci(tk)、ΔCi(tk)大小均可将A1,A2,…,Am相对比较。

合成时刻点tk评价值：

由时刻点t1，t2，…，tN合成总评价值：

越大则越优。

1.2.4 模型四：VIKOR法

（1）从横向差异分析。计算Ai群体效用Si(tk)、个体遗憾Ri(tk)：

将Ai进行折中:

（2）从纵向变化分析。计算ΔAi群体效用ΔSi、个体遗憾 ΔRi：

将ΔAi进行折中:

其中 ΔS-(tk)，ΔS+(tk);ΔR-(tk)，ΔR+(tk)取法与S-(tk)，S+(tk);R-(tk)，R+(tk)类似。

根据Qi(tk)或ΔQi(tk)进行排序；其值越小则说明Ai或Δ Ai越优。

合成时刻点tk评价值：

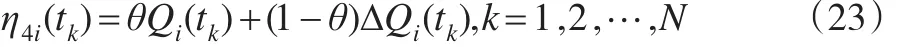
由时刻点t1，t2，…，tN合成总评价值：

越小则越优。

总之，由这些模型总评价值z1i,z2i,z3i,z4i，均能实现A1,A2,…,Am排序或择优。

2 实证应用

以医疗质量综合评价问题为载体，从多个年度、多个科室纵横向分析。围绕指标体系依次采集三维立体测量数据，对指标内涵或时刻点作用分别赋予权重，以经典方法为理论基础设计动态综合评价模型并检验可行有效性，为类似问题应用者提供参考。本文侧重方法实证而简化资料，当然也可以类推于更多时刻点、多层递阶指标体系的复杂情况。

2.1 数据选取

文献基础上选用代表性指标[6，7]：治疗有效率(%)c1、三日确诊率(%)c2、护理合格率(%)c3、抢救成功率(%)c4、诊断符合率(%)c5、病床使用率(%)c6、病床周转数(%)c7、日均门诊人次(数)c8、住院病死率(%)c9、院内感染率(%)c10和平均住院日(天)c11。c1～c8为效益指标、c9～c11为成本指标。指标内涵权重依次为0.048,0.078,0.042,0.108,0.054,0.06,0.068,0.088,0.078,0.192,0.184。针对潍坊市四所同级医院普外科A1～A4，采集2014—2016年指标测量数据，见表2。

表2 演示案例中三维立体测评数据

在三个年度全时段内，从所有科室从多个年度综合评价医疗质量，测评数据体现每个年度指标差异和前后年度指标变化信息。若指标变差或退步则惩罚、若指标变好或进步则激励。上述四种模型流程在Excel中逐步实现、编排计算并列举主要结果。

2.2 结果分析

由公式（1）进行预处理，计算年度之间指标变化量（2014年为基点而除外），见下页表3所示。

2.2.1 模型一：线性加权法

由公式（2）至公式（4）计算yi(tk)，Δyi(tk)，ηi(tk),N=3，m=5，n=11:

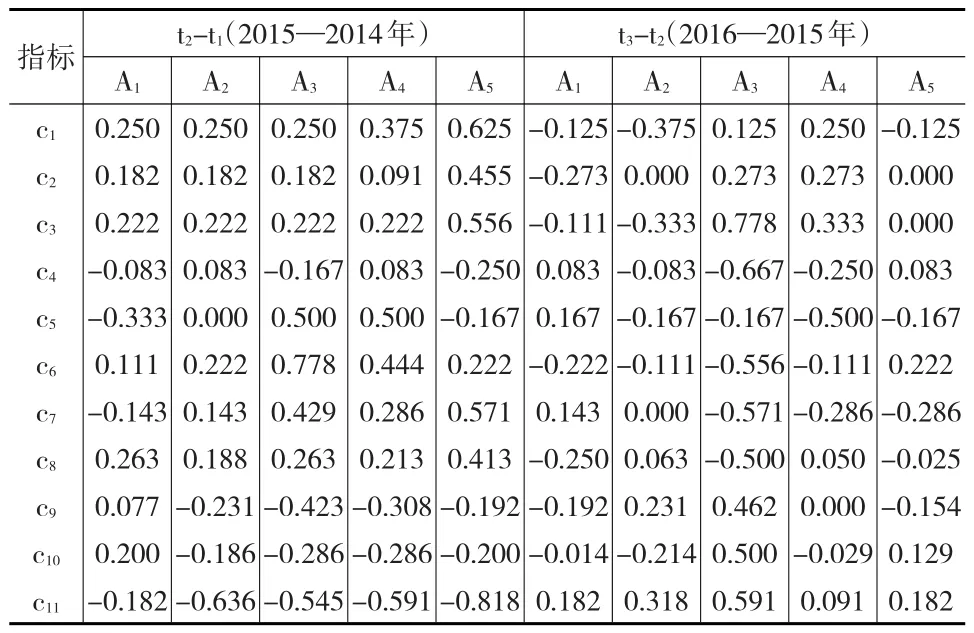
表3 年度之间指标变化量

由公式（5）计算各年度权重0.078,0.348,0.574。

由公式（6）计算z1i:0.319,0.261,0.268,0.250,0.185。

由线性加权动态综合评价法，按z1i由大到小优劣排序 A1＞A3＞A2＞A4＞A5。

正理想点A+=(1，1，…，1)、负理想点A-=(0，0，…，0)。

2.2.2 模型二：TOPSIS法

正理想点：ΔA+=(0.625,0.455,0.778,0.083,0.500,0.778,0.571,0.413,0.462,0.500,0.591);

负理想点：ΔA-=(-0.375,-0.273,-0.333,-0.667,-0.500,-0.556,-0.571,-0.500,-0.423,-0.286,-0.818)

由公式（12）计算z2i:0.540,0.495,0.495,0.484,0.430。

由TOPSIS动态综合评价法，按z2i由大到小优劣排序A1＞A2＞A3＞A4＞A5。

2.2.3 模型三：灰色关联法

由公式（17）计算η3i(tk):

由公式（18）计算z3i:0.490,0.473,0.466,0.465,0.440。

由灰色关联动态综合评价法，按z3i由小到大优劣排序A1＞A2＞A3＞A4＞A5。

2.2.4 模型四：VIKOR法

由公式（19）和公式（20）计算Si(tk),Ri(tk),Qi(tk):

由公式（21）和公式（22）计算ΔSi(tk),ΔRi(tk),ΔQi(tk):

由公式（24）计算z4i:0.206,0.585,0.516,0.536,0.703。

由VIKOR动态综合评价法，按z4i由小到大优劣排序A1＞A3＞A4＞A2＞A5。

经过比较，由四种医疗质量动态综合评价模型均可认为科室A1最优、科室A5最差。

当然，机理和结构视角不同会引起结论差异，应结合算法特点进行解析导读，见表4。

表4 模型算法特点及结论比较

3 讨论

综合评价问题多见固定时刻点由多个对象采集静态面板数据为依据，而系统动态发展特性导致更为复杂问题出现。本文从多个时刻点多个对象视角采集立体数据为基础，有静态情景改进设计为动态综合评价模型，验证可行性、比较有效性。基本思路是对指标赋予内涵权重、对时刻点赋予作用权重，从对象和时刻点角度全方位采集纵横向测量数据。指标权重系数也并非恒定不变而在必要时也可在时刻点之间动态修正。由指标动态变化情况获取变化量信息，横向差异和纵向变化信息反映于所有环节。从指标之间纵向变化信息利用来看，易平涛[8]由发展因子体现指标变化信息并提前修正测量数据用于模型计算；李美娟[5]将指标变化信息另外纳入模型，按差异或变化两类信息加权合成总评价值。前者易解释但算法复杂，后者较简便但二者比例分配主观，方法选用有待于进一步比较讨论。

本文以“先作静态评价、再按时间合成”为思路，参考指标差异或变化信息独立分析法[5]，以四种经典方法为基础理论设计动态综合评价模型并检验比较，TOPSIS法以全时段立体数据为基础，从指标本有信息或指标变化信息视角虚构正负理想对象，每个时刻点将所有对象按静态方式集结计算，每个对象与正负理想对象两个方向计算距离及相对贴近度。灰色关联法也是理想点逼近思路，区别之处是计算灰色关联度及相对贴近度，最后动态合并为排序结论。线性加权法兼顾指标差异或变化信息，在每个时刻点静态集结计算并将整个时间段动态合成，计算简便但不足是集结原理及信息合成解释力小。VIKOR法从“最大化群体效用”和“最小化个别遗憾”视角提出，将二者折中计算为评价值，也有特定功能和导向意义。这些方法充分利用对象和时间维度测量数据，体现一段时间内对象之间复杂情况，虽然理论视角、算法程序不同却都有适应性。由医疗质量问题载体验证卫生综合评价工作可行性扩展意义。TOPSIS和灰色关联分析法结论一致，与线性加权法和VIKOR法稍有差异。多种方法组合设计有助于结论之间收敛或一致，从而为实际决策者提供唯一评价结论。然而组合模型未从本质上提出新方法，而且组合结论含义难以解读而降低导向意义。综合评价复杂问题方法探索正引起交叉学科关注，也须在社会经济或医疗卫生应用问题中比较、检验和推广。