不同权力结构下考虑互惠偏好的闭环供应链定价策略
2018-10-17崔玉莹李瑞胜青岛大学商学院山东青岛266071
崔玉莹,李瑞胜 (青岛大学 商学院,山东 青岛 266071)
0 引言
闭环供应链中的成员定价策略是影响渠道成员收益的关键环节,因而引发了一系列该领域的研究,现有文献从不同的回收渠道、新制造产品与再制造产品的统一或差异定价机制等视角展开分析,得到若干管理学启示。如Savaskan等(2004)比较分析了三种回收模式下闭环供应链的定价策略及渠道利润,指出由零售商回收时闭环供应链的回收效率与系统绩效最高[1]。韩小花(2010)研究了闭环供应链回收渠道决策的主要影响因素是制造商之间的竞争程度;结果表明当竞争程度较高时,制造商选择直接回收旧产品;当竞争程度较低时,制造商委托零售商间接回收废旧产品[2]。其他研究还包括文献[3-5]等。
当前闭环供应链定价策略的研究大都以参与者为完全自利的理性经济人的前提,换言之,经济活动的所有决策者均只注重自身利益。然而,大量实证研究表明:经济活动中的竞争主体在现实中也会表现出非自利的心理偏好,如具有互惠偏好等。因此,在供应链运营管理的研究中,引入决策者的互惠等非理性行为因素,能够更贴近现实中的运作方案。
近年来已有学者将互惠偏好引入至供应链定价博弈模型的研究中,但大都集中于传统正向供应链领域。张红(2011)运用案例分析法对金山化工浆层纸生产联盟体中互惠共生界面的选择机制进行了分析[6]。林润辉(2014)研究了互惠偏好对回购契约协调效果和决策行为影响[7]。陈畴镛(2015)结合行为经济学家Rabin提出的互惠性偏好理论,对委托代理模型进行了行为经济学层面的拓展[8]。Du(2014)等研究探讨互惠偏好如何影响成员的决策和渠道的协调[9]。Xia(2017) 等研究互惠和碳减排行为如何影响供应链成员的决策以及系统效率[10]。Zhang(2017)等考虑追随者根据领导者的行为来评估领导者的意图,然后可以采取积极或消极的互惠行动,以调查零售商互惠行为对定价决策的影响[11]。
在逆向供应链或闭环供应链领域,赵琳(2016)将互惠利他偏好整合为两种偏好倾向的复合效用项,在此基础上建模分析该行为倾向对闭环供应链定价策略的影响机理[12]。张克勇(2015)再制造商回收模式下,研究了制造商和零售商为互惠偏好者的闭环供应链最优定价策略和利润,进而分析这种互惠偏好对决策行为和渠道效率的影响[13]。赵琳(2015)等考虑具有回报性质的互惠利他偏好情况,分析比较互惠性偏好引入前后闭环供应链的最优定价、各参与方的收益情况与主观效用,并通过数值Closed-loop Supply Chain Pricing Strategy Considering Reciprocal Preference under Different Power Structures仿真对结果加以验证[14]。其研究结果表明:双方互惠偏好会促使回收方提高废旧品回收价和回收量;各决策者的主观效用分别与对方的利他偏好呈正相关关系,且优于无互惠利他偏好情形,这说明决策者的互惠互利行为可以实现双方共赢。
由以上综述可知:学界对于传统正向供应链中利他和互惠行为的研究已较为普遍,但在闭环供应链领域尚处于起步阶段,目前仅有文献[12-14]对此有所涉猎,但也仅局限于制造商主导和制造商回收的情形。然而,随着近年来市场主导力量的变化,巨型零售商主导供应链以及双方力量均衡等情况在现实中已不鲜见。此外,由于零售商临近消费市场,对顾客信息的掌握也更为完善,零售商从事旧产品回收在一定程度上比制造商回收表现出更大的优势,因此本文在前人研究成果的基础上,探讨制造商主导、零售商主导和双方Nash均衡三种渠道权力结构下考虑决策者互惠偏好的零售商回收型闭环供应链定价策略是对已有研究有效的补充和延伸。
1 三种权力结构下考虑互惠偏好的闭环供应链定价模型
1.1 模型假设与参量说明
(1) 基本假设
考虑由一个制造商和一个零售商组成的两级闭环供应链系统,其中制造商负责产品的生产和再制造,并委托零售商进行产品销售和旧产品回收,此处假设再制造产品与新产品品质与价格均无差别。分别针对制造商主导、零售商领导以及Nash均衡博弈三种权力结构展开研究。
在制造商主导的市场结构中,制造商拥有绝对的主导权,即其首先制定批发价格,然后处于从属地位的零售商根据制造商的批发价制定自身的零售价格和回收率;在零售商主导的市场结构中,零售商占有绝对的主导权,即零售商先决定自身的零售价格和回收率,制造商根据零售商决策制定批发价格;在制造商和零售商Nash博弈中,双方同时决策,且均不能依赖对方的反应函数。
(2) 模型的参量说明
模型涉及的基本常量及符号说明如下:
cm:表示制造商利用新材料进行生产所需要的单位成本;cr:表示制造商利用回收品生产再造品所需要的单位成本;Δ:表示利用旧产品再制造所节省的成本,假设Δ=cm-cr>0;θR:零售商的互惠偏好系数;θM:制造商的互惠偏好系数;需指出的是θM>0,θR=0对应于制造商为利他偏好者、零售商为完全理性者的情形,θM=0,θR>0对应于零售商为利他偏好者而制造商为完全理性者的情形。w:表示零售商支付给制造商的产品批发价格,为制造商的决策变量;p:表示消费者支付给零售商的产品零售价格,为零售商的决策变量;τ:表示废旧产品的回收率(0≤τ≤1 ),为零售商的决策变量;CL:零售商的回收努力成本;b:表示制造商支付给回收方的回收转移价格;m:表示零售商销售产品的边际利润,则m=p-w;:表示j决策模式下成员i的利润;:表示j决策模式下成员i的效用;πj:表示j决策模式下的系统总利润;i:下标i∈{M,R,T },分别表示制造商、零售商和闭环供应链三种不同渠道;j:上标j∈{MS,RS,NS},分别表示制造商主导模式、零售商主导模式、纳什均衡模式。
在互惠偏好情形下,制造商的主观效用函数为:
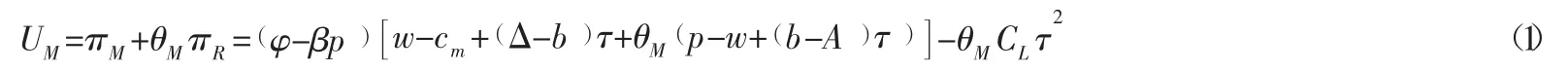
零售商的主观效用函数为:
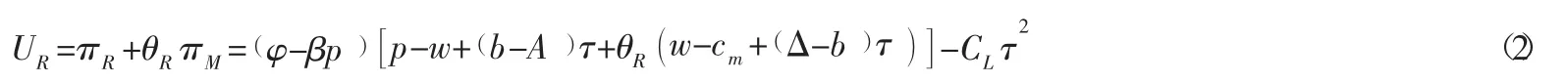
1.2 制造商—Stackelberg博弈
在制造商—Stackelberg博弈的市场结构下,考虑制造商和零售商进行如下阶段的动态博弈,由制造商先决定批发价格。博弈顺序为:
(1)制造商先决定批发价格w;(2)零售商再决定零售价格p和回收率τ。
上述博弈为完全信息动态博弈,可采用逆向归纳法进行求解子博弈精炼解。由=0,可得p(w),并由其一阶条件=0得到制造商主导模式下的最优批发价格和回收率:
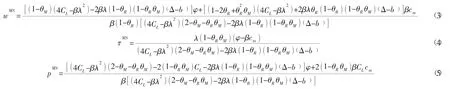
其中:λ=θRΔ+(1-θR)b。
从而进一步求得制造商的主观效用如下:

制造商还需确定最优的转移价格b*,由=0得:
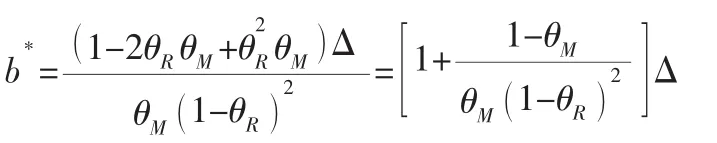
易知b*≥Δ,然而当b*严格大于Δ时制造商逆向渠道的利润为负,因而取值bMS*=Δ,将其代入式(3)至式(5)得:

MS模式下制造商、零售商的利润及效用以及渠道总利润和效用如表1中的第1列所示。
1.3 零售商—Stackelberg博弈
在零售商—Stackelberg博弈的市场结构中,考虑制造商和零售商进行如下阶段的动态博弈,由零售商先决定零售价格p和回收率τ。博弈顺序为:
(1)零售商先决定零售价格p和回收率τ;(2)制造商再决定批发价格w。
由于上述博弈为完全信息动态博弈,其均衡是子博弈精炼纳什均衡,同样可采用逆向归纳法来求解博弈。
把p=m+w带入式(1),将UM对w求导,整理后批发价格的最优反应函数为将w(p,τ)带入(2) 式由=0,可得:

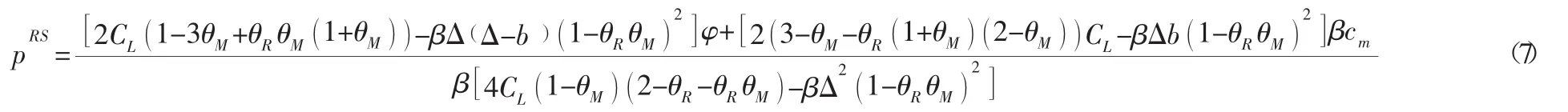
进而求得:
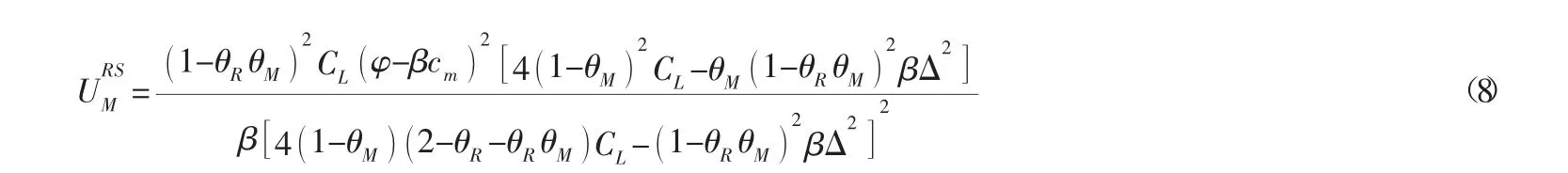
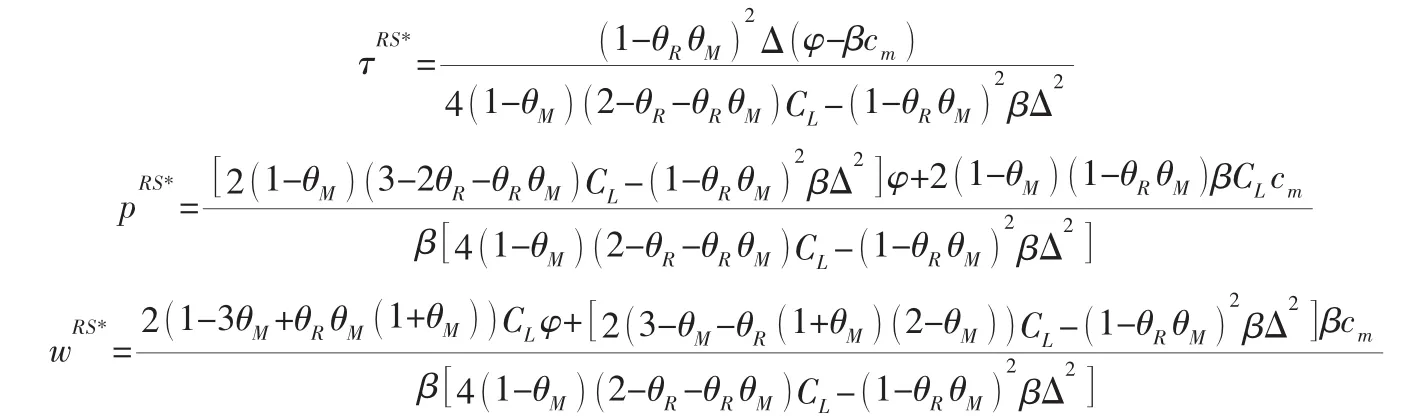
RS模式下制造商、零售商的利润及效用以及渠道总利润和效用如表1中的第2列所示。
1.4 Nash均衡博弈
在Nash均衡博弈的市场结构中,双方均不能利用对方的反应函数。即制造商决定批发价格w,同时零售商决定零售价格p和回收率τ。因而联立求解0即可得到双方决策。
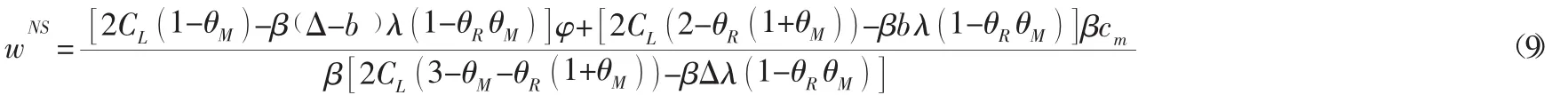
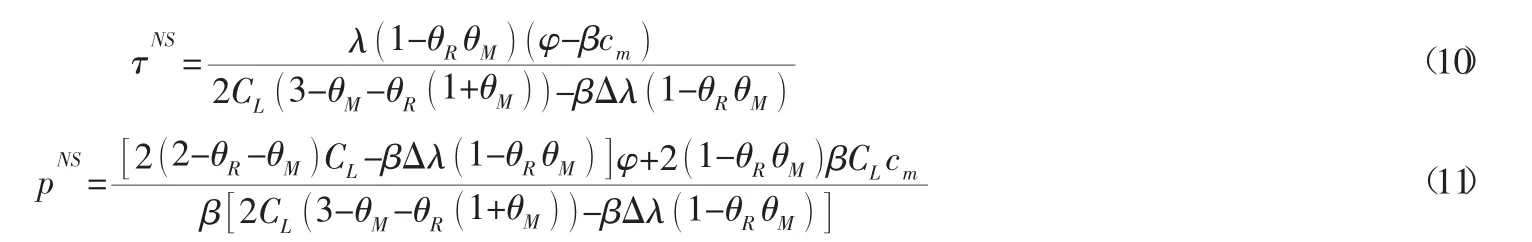
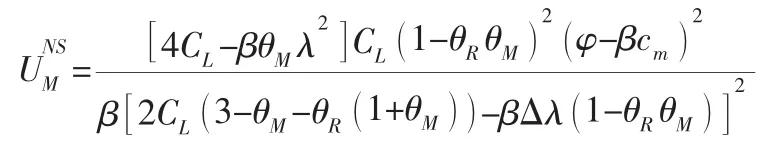
易知b*≥Δ,然而当严格大于Δ时制造商逆向渠道的利润为负,因而取值=Δ,将其代入式(9)至式(11)得:
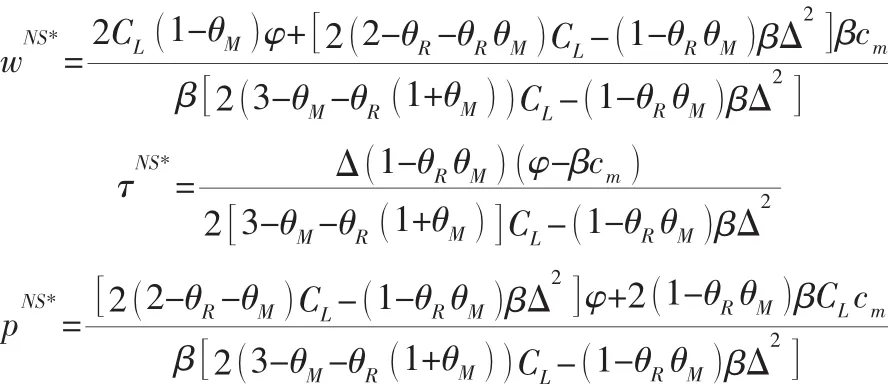
NS模式下制造商、零售商的利润及效用以及渠道总利润和效用如表1中的第3列所示。
为保证MS模式下的零售商利润非负,互惠系数θM应满足0<θM<1/3;同理,为保证RS模式下的制造商利润非负,互惠系数θR应满足0<θR<1/3。因此,为便于后续对三种主导模式下均衡解的比较分析,给定θM与θR的合理区域为:Ω={(θM,θR)|0≤θM<1/3,0≤θR<1/3}。
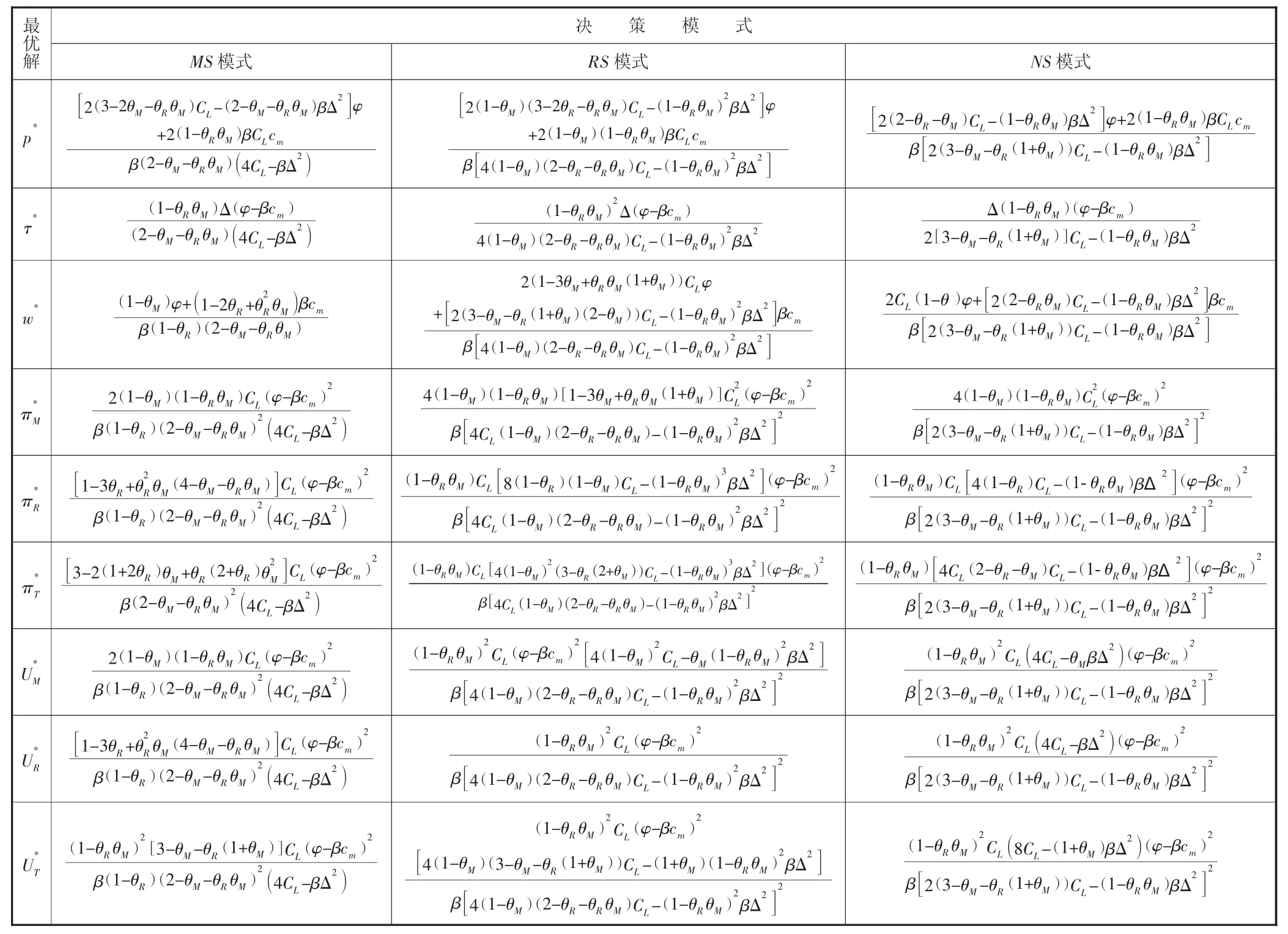
表1 三种权力结构下考虑互惠偏好的闭环供应链均衡结果
命题1:三种权力结构下零售商最优回收率均与双方的互惠偏好程度正相关。
证明:将各均衡解分别对θM与θR求一阶偏导数即可得此结论,限于篇幅略。
命题1表明当零售商和制造商均有互惠偏好的行为时,以上三种结构下均会引起零售商回收力度增加,这样会不仅利于废旧物品的有效回收资源再利用,而且还有利于环境的保护。
2 具有互惠偏好成员的决策均衡解的对比分析
由于对双方互惠偏好下三种权力结构的闭环供应链均衡解、利润与效用的比较较为复杂,以下将通过数值算例对回收率、产品售价、渠道成员利润与效用进行比较分析。具体参数取值依次为市场容量φ=1000,价格敏感系数β=5,回收投资成本CL=10000,生产成本cm=100,再制造成本cr=50,则成本节约Δ=50,根据第二章的结论知b=Δ。制造商与零售商双方的稳定合作区域为Ω={(θM,θR)|0≤θM<1/3,0≤θR<1/3 }。具体结果如图1至图8所示。
2.1 双方互惠偏好程度对回收率的影响
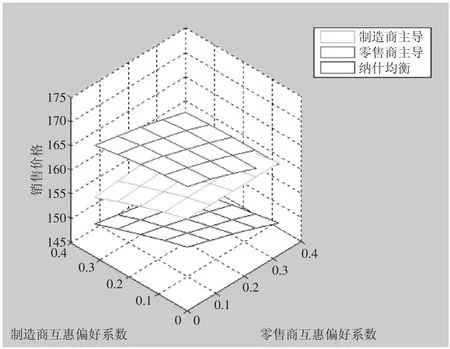
图2 双方互惠偏好程度对销售价格的影响
由图1可见,在制造商和零售商稳定互惠合作区域内,制造商与零售商Nash博弈时的回收率最高。在两种Stackelberg博弈模型比较时:
当制造商和零售商互惠程度均较低时,M主导模式下的闭环供应链回收率较高;
当制造商和零售商互惠程度均较高时,R主导模式下的闭环供应链回收率较高;
当制造商互惠程度较低而零售商互惠程度较高时,M主导模式下的闭环供应链回收率较高;
当制造商互惠程度较高而零售商互惠程度较低时,R主导模式下的闭环供应链回收率较高。
2.2 双方互惠偏好程度对产品价格的影响
通过数值仿真分析双方互惠偏好程度对零售商产品回收率的影响,结果见图2。由图2可见,在制造商和零售商稳定互惠合作区域内,制造商与零售商Nash博弈时的产品价格最低。在两种Stackelberg博弈模型比较时,当制造商互惠程度较低而零售商互惠程度较高时,M主导模式下的产品价格较高;在其余绝大部分区域中,R主导模式下的产品价格较高。
2.3 双方互惠偏好程度对制造商利润和制造商效用的影响

图3 双方互惠偏好程度对制造商利润的影响
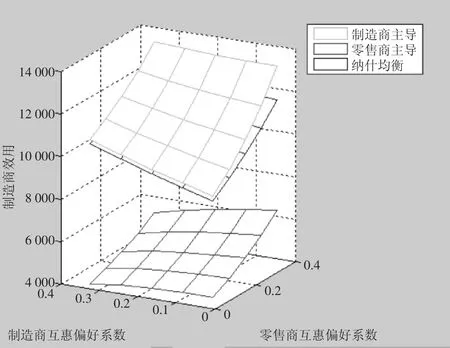
图4 双方互惠偏好程度对制造商效用的影响
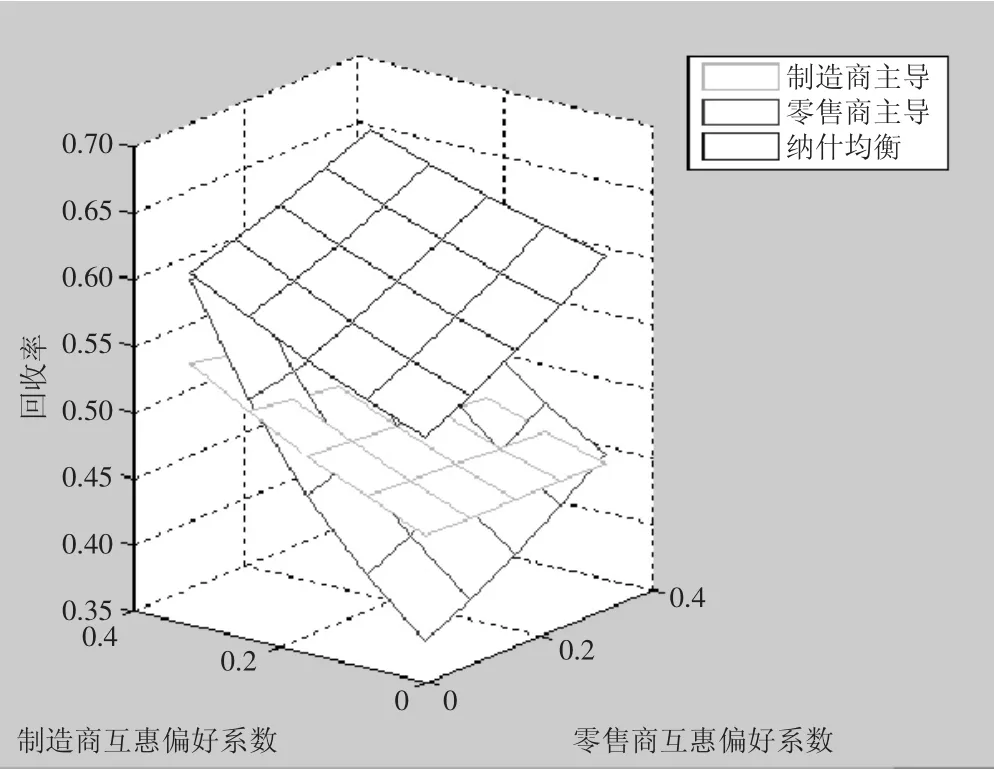
图1 双方互惠偏好程度对回收率的影响
由图3可知,在制造商和零售商稳定互惠合作区域内,M主导模式下的制造商利润最高,制造商与零售商Nash博弈时次之,R主导模式下的制造商利润最低。由图4可知三种权力结构下制造商效用的比较结果与制造商利润的结果类似。此外,当制造商的互惠偏好因子较高而零售商的互惠偏好因子较低时,无论在何种权力结构下,制造商的利润和效用均较其他区域更低;相反,当制造商的互惠偏好因子较低而零售商的互惠偏好因子较高时,制造商的利润和效用均较其他区域更高。
2.4 双方互惠偏好程度对零售商利润的影响
由图5可知,在制造商和零售商稳定互惠合作区域内,R主导模式下的零售商利润最高,制造商与零售商Nash博弈时次之,M主导模式下的零售商利润最低。由图6可知三种权力结构下零售商效用的比较结果与零售商利润的结果类似。此外,当零售商的互惠偏好因子较高而制造商的互惠偏好因子较低时,无论在何种权力结构下,零售商的利润和效用均较其他区域更低;相反,当零售商的互惠偏好因子较低而制造商的互惠偏好因子较高时,零售商的利润和效用均较其他区域更高。
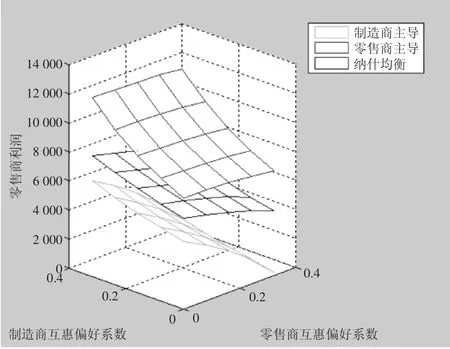
图5 双方互惠偏好程度对零售商利润的影响
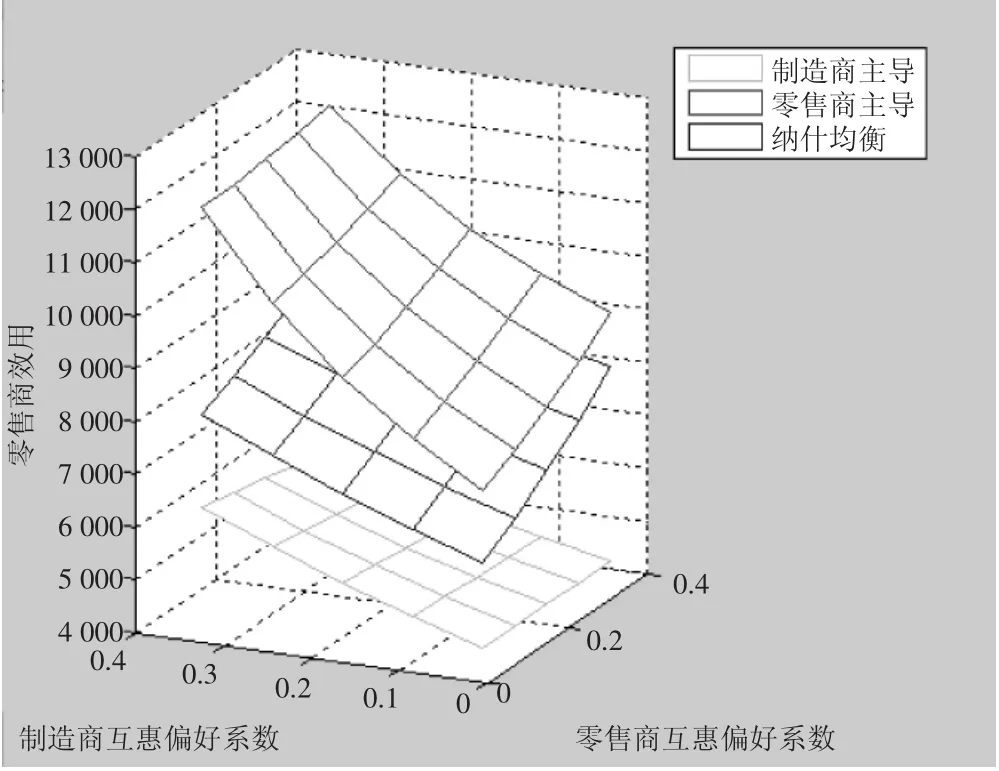
图6 双方互惠偏好程度对零售商效用的影响
由图7可知,在制造商和零售商稳定互惠合作区域内,Nash均衡博弈下的系统总利润最高,两种Stackelberg博弈模型下的系统总利润取决于双方的互惠偏好程度,在绝大部分区域内均是M主导模式下的系统总利润更优(尤其当制造商的互惠偏好因子较高而零售商互惠偏好因子较低的情形下),仅当制造商的互惠偏好因子较低而零售商的互惠偏好因子较高的极小范围内,R主导模式下的系统总利润更优。由图8可知三种权力结构下系统总效用的比较结果为Nash均衡博弈时最高,其次是M主导模式,最次是R主导模式。
从以上所有分析可知:从系统总利润、消费者利益以及环境绩效的角度,作为回收方的零售商主导闭环供应链最为不利。
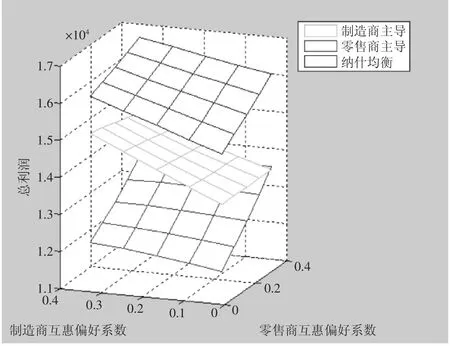
图7 双方互惠偏好程度对系统总利润的影响
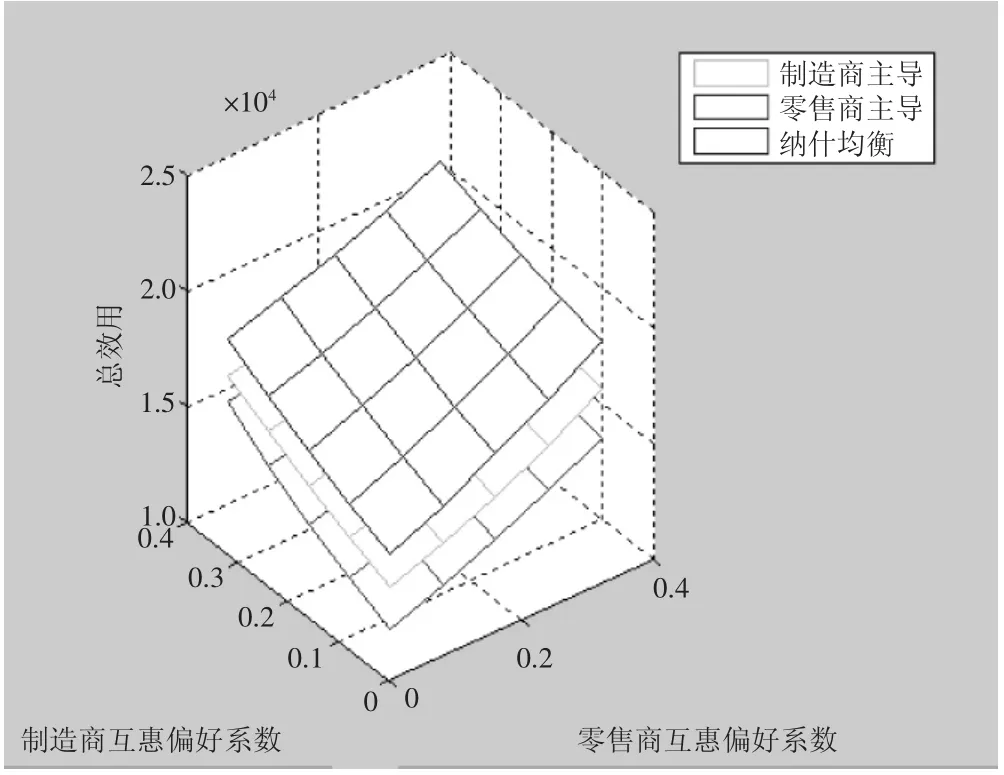
图8 双方互惠偏好程度对系统总效用的影响
3 结论
当前闭环供应链定价策略的研究大多是以决策者完全理性为前提,然而行为运筹学的研究表明:现实世界错综复杂,人们很难做出完全理性的决策,往往是有限理性的,因而非理性行为因素引入到闭环供应链中具有一定的理论和现实意义。
本文在考虑互惠偏好的背景下研究了闭环供应链的定价策略:当双方均为互惠偏好者时,在制造商和零售商的稳定互惠合作区域内,Nash均衡博弈时的回收率最高,两种Stackelberg博弈时的回收率取决于双方的互惠偏好程度。当制造商和零售商互惠程度均较低时,制造商主导的闭环供应链回收率较高。当制造商和零售商互惠程度均较高时,零售商主导的闭环供应链回收率较高。当制造商互惠程度较低而零售商互惠程度较高时,制造商主导的闭环供应链回收率较高。当制造商互惠程度较高而零售商互惠程度较低时,零售商主导的闭环供应链回收率较高。双方Nash博弈时的产品价格最低。在两种Stackelberg博弈模型比较时,当制造商互惠程度较低而零售商互惠程度较高时,制造商主导的产品价格较高;在其余绝大部分情形下,零售商主导的产品价格较高。Nash均衡博弈下的系统总利润最高,两种Stackelberg博弈模型下的系统总利润取决于双方的互惠偏好程度,在绝大部分情形下均是制造商主导的系统总利润更优,仅当制造商的互惠偏好因子较低而零售商的互惠偏好因子较高的极小范围内,零售商主导的系统总利润更优。综上,当双方均为互惠偏好者时,从系统总利润、消费者利益以及环境绩效的角度,作为回收方的零售商主导闭环供应链最为不利。
