“多次使用同向不等式的可加性”可导致错误？

周惠

西藏民族大学附属中学 陕西咸阳 712000

对于不等式有如下的性质：

若a＞b,c＞d则a+c＞b+d（非严格不等式）

我们可以把上述性质加强一下

若 a≥b,c≥d 则a+c≥b+d（当且仅当a=b且c= d 时等号成立）（非严格不等式）

它的正确性毋庸置疑！

问题的提出：设 f (x) =ax+bx，若2≤f(1)≤4，则f(-2)的取值范围是______

由此可得4≤f(-2)=4a- 2b≤11

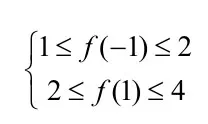
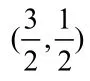
以上两种解法不同，结果也不同，从现有资料看，大家都意识到解法一是错误的，解法二正确的，但对解法一错误的原因解释为“多次使用同向不等式的可加性而致误”，这种解释显然是不够准确的，我们不禁要问:一个正确的定理会因使用次数的多少而产生错误吗？

答案是肯定的：不会！

那么问题到底出在哪里呢？

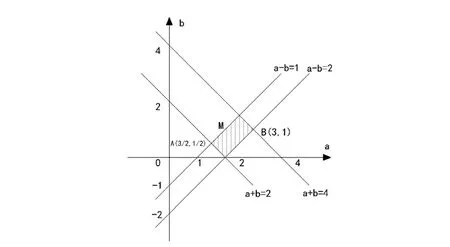
我们把解法一推得 (2)f- 范围的 ,ab的区域N也在坐标系中表示出来如图

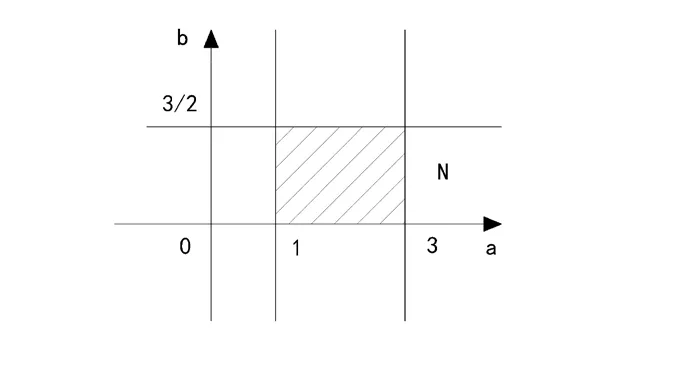
我们再来看本题的一个解法以供参考：

解法三：

所以 f ( -2) = 4a - 2 b = 3 f ( -1) + f (1)

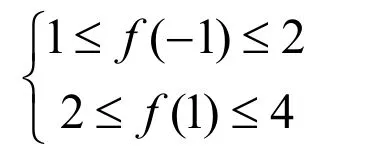
所以5 ≤ 3f ( -1)+ f(1) ≤ 10

即5 ≤ f(-2)≤10

这种解法是把 ,ab作为相关关系的来应用的，没有分割a与b之间的关系，因此与解法二结果相同，解法正确，可见同向不等式的可加性多次使用并没有问题，错误原因在于没有考虑变量的整体性以及等号成立的条件，所以在应用同向不等式相加的性质时，一定要明确等号成立的条件是什么？不等式中的变量是否同增减，范围是否会扩大，多个不等式是否同时取得不等式成立等等,要重视思维的严谨性和严密性。