基于全连接和LSTM神经网络的空气污染物预测
2018-10-16吴艳兰
韩 伟,吴艳兰,任 福
(1. 武汉大学 资源与环境科学学院,湖北 武汉 430079;2. 安徽大学 资源与环境工程学院,安徽 合肥 230601)
0 引 言
空气质量问题在经济发展迅速的今天愈发引起人们的关注,大范围、长时间、高浓度污染状况频发,严重影响人们生产生活以及身体健康.定量描述空气质量状况对于地区空气污染预防及制定相对对策意义重大.在国内,定量描述空气质量状况主要有两个指数[1],一个是空气污染指数(Air Pollution Index, API),另一个是空气质量指数(Air Quality Index, AQI).在2012年政府出台的相关规定中,将AQI替代原有的API成为新的空气质量标准.AQI作为定量描述空气质量状况的常用指标,是一种非线性无量纲指数,其数值越大、级别越高、表征颜色越深,说明空气污染状况越严重,对人体的健康危害也就越大.然而AQI的计算结果很大程度上取决于相应地区空气质量分指数及对应的污染物项目浓度指数表,因而对于AQI的计算具有极大的地区效应[1].为了摆脱AQI的地区效应,对AQI分级计算参与的空气污染物SO2、NO2、PM10、PM2.5、O3、CO等6种的浓度值的预测是十分必要的.
空气污染物预测是根据历史污染物的数据,气象数据等进行次日空气污染物的预测.在应用研究中,常见的主要是基于理论的方法和基于统计的方法[2-3].基于理论的方法是物理化学过程中的确定性预测方法,利用数学方法建立大气污染浓度在空气中的稀释扩散的数值模型,通过计算机高速计算来预报大气污染物浓度在空气中的动态变化.国外空气污染预报工作起步较早,目前国际上已经开发出多种数值预报的空气质量模型,如城市尺度的城市大气质量模型(Urban Airshed Model,UAM)、区域多尺度空气质量模型(Community Multiscale air quality, CMAQ)等,在科研领域中得到了广泛的应用.在国内,学术界也对空气质量预测的问题进行了深入的研究.中国科学院的雷孝恩建立了对流层高分辨率化学预报模型,该模型可预报对流层内多种气体污染物的时空分布及演变过程.中国气象科学研究院的徐大海建立了大气平流扩散的非静稳多箱模型,该模型可以预报空气污染潜势和污染指数[4].还有中国科学院大气物理研究所的王自发建立了嵌套网格空气质量预报系统[5]和中国气象局沈阳大气环境研究所在气象中尺度数值预报模型MM5和ADMS城市模型大气扩散模型的基础上[6]建立的城市空气质量预报系统.尽管在理论上污染数据准确,方程模型全面,该方法能得到很高的准确度,但是巨大的计算量和数据收集的偏差仍然影响着模型的预测[4].
基于统计的方法也是近几年来比较热门的方法,是以统计学为基础,通过分析历史空气污染数据,对未来的趋势进行预测.由于其成本低,快捷,简单的特点,受到许多研究者的关注.常见的一些预测模型包括多元回归模型[7],时间序列模型[8-9],神经网络模型等[3-4,10-17],其中非神经网络模型需要做出假设分析,挖掘对预测结果存在影响的特征因子,在众多特征因子与预测结果中建立相应的数学关系,存在一定的主观性,较为复杂.而神经网络模型能够像人类大脑一样自动学习到相关的特征,建立出相应的预测模型,在精准度上得到了一定的改善,但训练时间较长,泛化效果较差.
在神经网络对空气污染物预测的研究中,更多的注重于单一神经网络结构的构建,本文正是针对神经网络的高精准度,同时利用不同模型的混合能够改善单一模型的精度和泛化性的特性,借助Keras和tensorflow神经网络框架,构建了基于全连接神经网络和LSTM神经网络的空气污染物预测混合模型.
1 基于全连接神经网络的空气污染物预测模型
神经网络[3-4,10-17]是一种模仿生物神经网络(动物的中枢神经系统,特别是大脑)的结构和功能的数学模型或计算模型,用于对函数进行估计或近似.神经网络由大量的人工神经连接进行计算.大多数情况下人工神经网络能在外界信息的基础上改变内部结构,是一种自适应系统.现代神经网络是一种非线性统计性数据建模工具.
1.1 全连接神经网络
神经网络包含输入层、隐藏层、输出层,当相邻层神经元两两相连时,即构成全连接神经网络.它的目标是近似某个函数f*.如对于分类器,y=f*(x)将输入x映射到一个类别y.它定义了一个映射,如下:

通过学习参数θ的值,使它能够得到最佳的函数近似.
全连接神经网络包括线性部分和非线性部分.对于输入向量x=[x1,x2,…,xn]T,其经过隐含层,先得到线性输出向量z=[z1,z2,…,z3]T,主要通过权重向量W与偏置向量来确定的,也正是神经网络需要学习的参数,即按下式计算:

在得到线性输出向量后,利用非线性函数对输出向量进行转换得到隐含层的输出向量h=[h1,h2,…,hn]T或者输出层的输出向量y=[y1,y2,…,yn]T,在神经网络中这种非线性函数也叫做激活函数,常见的主要是Relu函数和sigmoid函数,其形式如下:
Relu函数:

Sigmoid函数:

全连接神经网络整体结构如图1所示,其本质就是通过参数和激活函数拟合已知特征与目标之间的关系.
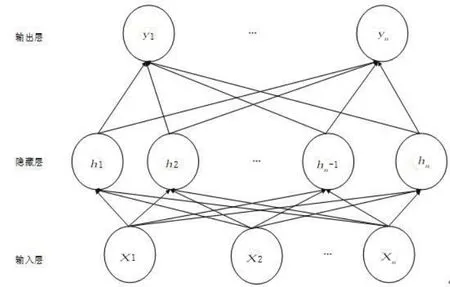
图1 全连接神经网络结构Fig.1 The structure of full-connection neural network
其中,[x1,x2,…,xn]是输入层的输入值,[h1,h2,…,hn]是隐藏层的输出值,[y1,…,yn]是输出层的输出值,输入层和隐藏层使用的激活函数是relu函数,而输出层采用的是Sigmoid激活函数.该神经网络能够较为准确地捕捉数据间的特征关系,预测精度较高,但是由于每个神经元都相互连接,训练的参数较多,对硬件的要求较高.
1.2 基于全连接神经网络的预测模型
1.2.1 模型数据
为了更加精确地预测次日空气污染物的浓度值,其中空气污染物包括SO2、NO2、PM10、PM2.5、O3、CO,模型中考虑过去七天的空气污染物浓度值和大气情况等138个特征(7天),这138个特征包括过去七天中每天的空气污染物和大气特征.对于大气特征包括平均日温、最高日温、最低日温、露点温度、平均湿度、最高湿度、最低湿度、降雨量、海平面气压、风速、最快风速、能见度,具体特征见表1.

表1 一天的特征变量及符号表示Tab.1 The representation of features and symbols in a day
模型的输出是预测当天的空气污染物.该模型以武汉市2013年12月2日至2017年8月14日之间接近4年的数据作为模型的数据来源.
1.2.2 模型结构设计
鉴于已知的特征数据,输入层是138维经过归一化处理的向量,为了避免过拟合以及经过实验验证,模型选择了两层隐藏层,第一层隐藏层设置了50层过滤器,并使用激活函数Relu函数进行第一层隐藏层的输出,第二层隐藏层设置了25层过滤器,并使用激活函数Relu函数进行第二层隐藏层的输出,最后输出层输出6维归一化后的目标值,对目标结果进行归一化逆变换得到最终的预测结果,其中最后输出层与分类器模型不同的是预测结果并未使用激活函数,原因是回归模型最终得到的是一个目标值,而不是类别的概率,同时使用两层隐藏层是为了让神经网络能够学习到更多的变量特征且避免更多隐藏层对数据的过度拟合.过滤器相当于特征映射,逐层的降低是为了让数据归一化到最后的目标,在训练的过程中通过设置不同的过滤器数目来调整预测值与目标值的差距.
模型的训练主要包括模型参数的初始化和参数的微调.在参数初始化过程中,损失函数的选择与模型任务息息相关,由于空气污染物预测属于回归预测,因而损失函数选择的是均方根误差,其公式如下:
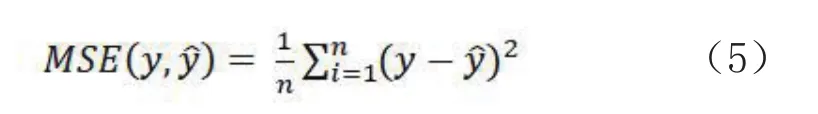
模型的目的就是最大化地减少损失函数的值,从而调整每个参数的值,因而模型选择的优化方法是Adam算法,Adam算法根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整针对每个参数的学习速率.Adam也是基于梯度下降的方法,但是每次迭代参数的学习步长都有一个确定的范围,不会因为很大的梯度导致很大的学习步长,参数的值比较稳定.
同时在训练时,模型训练结果的评价标准采用平均绝对百分误差MAPE,其值越接近于0,预测的准确度越高,其公式如下:
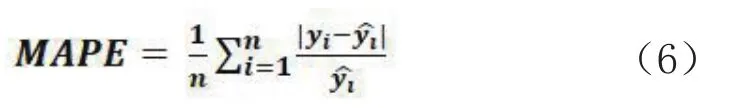
经过多次试验比较,不断修改学习速率的大小以及Adam算法其他参数,以保证最后的结果趋近于目标值,学习到更加精确的权重.
2 基于LSTM的空气污染物预测模型
2.1 LSTM神经网络
LSTM神经网络[3,15-16]即Long Short Term网络,属于循环神经网络RNN的一种,可以学习长期依赖的信息.RNN的关键点之一就是他们可以用来连接先前的信息到当前的任务上,如使用过去的视频段来推测对当前段的理解,从理论上可以解决长期依赖的问题,但在实践中肯定不能够成功学习到这些知识.而LSTM却没有这种问题,它通过刻意的设计来避免长期依赖问题.记住长期的信息在实践中是LSTM的默认行为,而非需要付出很大代价才能获得的能力.其具体结构如图2所示.LSTM与RNN的主要区别在于其算法中加入了一个判断信息有用与否的"处理器",这个处理器作用的结构被称为cell.
一个cell当中被放置了三扇门,分别叫做输入门、遗忘门和输出门.一个信息进入LSTM的网络当中,可以根据规则来判断是否有用.只有符合算法认证的信息才会留下,不符合的信息则通过遗忘门被遗忘,从而有效地解决长期依赖的问题.

图2 RNN和LSTM结构的对比[18]Fig.2 The contrast of RNN and LSTM structure
2.2 基于LSTM神经网络的预测模型
2.2.1 模型数据
该模型使用的数据跟全连接神经网络不同,模型考虑更多的是时间上的关联性,所使用的数据仅仅只有过去的空气污染物的浓度值,没有加入历史的大气数据,通过对历史SO2、NO2、PM10、PM2.5、O3、CO 6种空气污染物的浓度值在时间维度上的分析,预测次日这几种污染物的准确浓度值.其中,前一天6种空气污染物的浓度值作为模型的输入,后一天6种污染物的浓度值作为模型的输出,形成一组训练集或者测试集.
2.2.2 模型结构设计
模型的结构主要取决于LSTM神经网络的结构,其核心结构包括输入层、LSTM层、输出层,其中LSTM层是整个模型的关键,通过前一天空气污染物的情况来预测第二天的空气污染物情况,再通过第二天的空气污染物情况来预测第三天的情况,以此类推,将历史的空气污染情况逐渐向前传递,cell中的遗忘门起到控制内部状态信息的作用,门的输入为上一个时刻点的隐藏节点的输出以及当前的输入,激活函数为sigmoid,因为sigmoid的输出为0~1之间,将内部状态节点的输出与遗忘门的输出相乘可以起到控制信息量的作用,从而保证模型能够吸收历史空气污染情况的有用信息,忽略无用的信息,并充分节省所使用的资源和时间.其具体结构如图3所示.

图3 LSTM预测模型简化结构Fig.3 The simplif i ed structure of LSTM prediction model
图3 中,左边是6种空气污染物前一天的浓度值,作为LSTM模型的输入,右边是后一天的浓度值,作为模型的输出,对于原始数据将相邻两天的污染物的浓度值分别作为模型的输入与输出,从而作为一组训练集或者测试集.
同时为了保证最后模型能够进行有效的对比,该模型使用的优化算法也是Adam算法,评价标准依然采用平均绝对百分误差MAPE,但是在实验基础上,参数的具体数值会有所区别.
3 混合预测模型
混合预测模型是将多个模型得到的结果进行融合得到一个更好更全面的模型,实质是减小偏差(bias)和方差(variance),使模型达到最优的结果,bias与variance的关系如图4所示.

图4 偏差与方差的关系图[19]Fig.4 Diagram of relationship on bias and variance
其中,多个模型融合的方式有多种,包括投票,平均化或者用另一种算法进行再训练等,不同的融合方式适合于不同的情形.对于空气污染物预测,其本身属于回归问题,并且训练的基模型只有全连接神经网络预测模型和LSTM预测模型两种,基模型数量较少,因而对基模型进行复杂融合方式容易造成结果过拟合,利用简单的线性叠加更加适合,避免过拟合问题的发生.尽管两种基模型在一定程度上均有一定的预测作用,但是从学习特征的角度是有所区别的,全连接神经网络更加趋于输入数据彼此的影响,而LSTM模型更大程度上考虑到了时间上的关联性,将两种模型进行融合能够有效扩大假设空间,避免模型陷入局部极小,因而将两种模型的结果进行线性叠加将会获得更好的效果.
将训练数据分成两部分,一部分用来训练上述的全连接神经网络和LSTM网络预测模型,另一部分用来训练两种模型输出结果后的线性模型,也就是混合预测模型,其具体公式为:

其中,y代表最后混合预测模型结果,x1代表全连接神经网络的预测结果,x2代表LSTM神经网络的预测结果,a,b,c正是要学习的参数,代表权重和偏置值.
将两种预测模型进行线性叠加不仅能够提高一定的准确度,而且可以降低预测结果的方差,提高泛化能力.
4 实验分析与验证
在以武汉市2013年12月2日至2017年8月14日之间接近4年共计1 350条数据为例时,通过对这3种模型进行学习训练,以平均绝对百分误差MAPE为评价标准(公式(5)).其中武汉市的数据是在数据网站中国空气质量在线监测分析平台(https://www.aqistudy.cn/historydata)和weatherunderground平台(https://www.wunderground.com/history/)通过爬虫获取的,数据特征见表1,并随机将数据中的80%作为训练集,剩下的20%作为测试集,进行了10次随机实验,经过前期的训练和预测,10次随机实验结果的规律基本保持一致,所以本文选取了其中一次实验进行分析与验证.这次实验中3种模型在6种空气污染物中的表现与真实情况进行对比分析如图5所示.

图5 各预测模型结果Fig.5 The results of all predicted models
散点图中蓝色和红色分别代表各种污染物浓度值的真实值和预测值,整体上看,各种空气污染物的真实分布与预测分布是一致的,甚至在污染物浓度值出现极值的情况下也能够捕捉到相关的信息,但是在极值点的情况下,LSTM模型和混合预测模型明显优于全连接神经网络,但是整体上散点图中无法观看到3种模型拟合的差异性以及哪种模型具有更高的精准度.所以,为了更加显著地显示混合模型对于单一模型的优势,本文采用评价标准平均绝对百分误差MAPE(公式(6))来具体观察3种模型的差异性,因为空气污染物预测是一个回归问题,不能使用准确率,召回率等一些分类指标,而相对于其他回归指标,MAPE指标不仅能够表明每一种空气污染物预测值与真实值的差距,而且能够将不同污染物的差距放在同一个标准下进行比较对比,避免了不同污染物因为在空气中占比差异导致最后结果不在同一个标准范围.最后3种模型在测试集上的MAPE平均预测结果见表2.

表2 随机测试集上的平均测试结果Tab.2 The average test results of randomized test set
从模型在预测集上的平均绝对百分误差的结果中可以看出3种模型在6中空气污染物的预测中均有较高的准确度,3种预测模型在NO2和CO两种空气污染物上的预测准确度均是最好的,表明这两种空气污染物较为稳定,易于挖掘出它们的变化趋势,而PM10、PM2.5、O33种空气污染物在3种模型中表现是较好的,说明这3种空气污染物具有一定的稳定性,通过历史数据的分析能够对次日污染物的预测做出基本的掌控,最后SO2在全连接神经网络预测模型和LSTM神经网络预测模型两种单预测模型的预测结果中表现的都不是太好,但是在混合预测模型上得到了10%以上的提升,因而从整体上说混合模型较前两种单模型在6种污染物上的预测精度均有一定提升,具有一定的应用价值,而且泛化能力得到了一定的提高,各种污染物的平均绝对百分误差的差距缩短了,因而实际的效果会更好.
5 结束语
本文针对空气环境质量数据,利用神经网络在环境方面的应用,提出了一种基于全连接神经网络与循环神经网络LSTM的混合预测模型.该模型是以两种神经网络预测模型作为基础,经过线性叠加,建立一种对次日空气污染物包括SO2、NO2、PM10、PM2.5、O3、CO等6种污染物浓度值的预测.最终通过实验得到以下结论:
1)通过全连接神经网络模型,过去七天空气污染物包括SO2、NO2、PM10、PM2.5、O3、CO等污染物浓度值和大气数据包括湿度,风速等指标数值是可以预测次日SO2、NO2、PM10、PM2.5、O3、CO等空气污染物浓度值.
2)通过时序神经网络LSTM模型,过去一天空气污染物的浓度值可以预测次日空气污染物的浓度值.
3)混合预测模型可以结合全连接神经网络模型和时序神经网络LSTM模型,对次日空气污染物进行浓度值的预测.
4)混合预测模型在空气污染物的预测上要比单一模型,如全连接神经网络模型和时序神经网络LSTM模型的预测精度更高,效果更好,具有更高的应用价值.
本文在建立模型的过程中,由于硬件和数据量的限制,无法对模型进行更加复杂的设计,包括对神经网络深度的探索,正则化的处理等,下一步将收集更大数据量,在改善硬件环境下进行更深层次的探索与分析.
