一种基于地球剖分网格的区域面积计算方法
2018-10-16齐澄宇程承旗濮国梁
齐澄宇,程承旗,濮国梁,陈 波
(1. 北京大学 遥感与地理信息系统研究所,北京 100871;2. 北京大学 工学院,北京 100871)
0 引 言
地球剖分网格是一种科学简明的空间参考系统,是地球信息数据的离散化、准确化、系统化的表现[1].在地球剖分的思路上,产生了多种全球离散格网系统(Discrete Global Grids System, DGGS)[2].Goodchild、郭华东等认为,DGGS采用预先计算的瓦片结构优化本地计算,提高使用中的细节管理水平,这是"虚拟地球最吸引科学工作者的特点之一"[3].特别是随着对地观测能力的增强,空间数据体量迅猛增长.利用网格进行数据组织、用带有位置信息的网格编码替代经纬度来记录数据的位置属性,成为多源异构空间大数据解决方案.其思路在于,在适用于大数据的新型列数据库中,使用网格编码作为数据索引主键,实现数据与位置的自动关联.相关研究包括真三维数据表达[4]、警用大数据[5]、遥感大数据[6]、空间对象快速可视化[7]等.
地表区域面积计算一直是测绘科学的一个重要问题,在国土面积测量、土地资源管理、民政、遥感、减灾等方面都有实际应用.在计算机辅助软件产生之前,基于地图数据的面积测量常用的方法是网格法、求积仪法.地理信息系统产生之后,在常用的矢量和栅格两类数据模型下,借助计算机,可以方便地进行面积计算.如矢量模型以点为最基本的实体组成.计算矢量多边形的面积,一种可行的方法是根据点的坐标借助格林公式[8]精确计算.
网格型地理信息系统有望凭借其在处理大体量多源异构数据中的优势,成为大数据地理信息系统的解决方案,基于网格的空间量算变得尤为重要.在剖分框架下,实体和数据以剖分网格组织,实体的面积就是其对应的网格集的面积之和.问题在于,球面空间与欧氏空间不同胚,导致同一层级剖分网格的面积不尽相同.以等经纬度剖分网格为例,由于不同纬度下相同经度差对应的地表长度不同,因此同一层级的网格由赤道到两极,面积变小.计算剖分网格集对应的地表范围面积,常常需要先将网格对应回经纬度范围,再借助积分方法求解,地表区域面积计算效率低.
针对以上问题,本文提出了一种新的地表面积计算方法,以GeoSOT地球空间剖分参考框架为基础,根据GeoSOT剖分网格几何特性,结合地表区域面积计算的需求,构建全球网格弧长数据库,以查表求和方法取代经纬度积分方法,实现在该框架下地表区域面积快速、精确计算,有望应用于测绘、遥感、减灾、国土资源管理等诸多领域.
1 GeoSOT地球剖分方案
基于空间信息剖分组织理论,北京大学程承旗团队[9]提出"2n一维整型数组的全球经纬度剖分参考网格"(Geographic Coordinate Subdivision Grid with One Dimension Integral Coding on 2n-Tree,简称GeoSOT),以探寻建立一种空间信息或数据组织的专用网格,并能够与现有的主要空间数据组织网格有很好的区位关联和尺度聚合关系;为空间信息的统一区位组织和区域关联调度,构建一种更适合空间信息组织的区位标识体系.GeoSOT全球剖分方案提出之后,很多学者针对多源数据在GeoSOT剖分参考框架下的表达、组织、管理、分发等技术与应用层面展开了深入研究,如气象水文[10]、减灾[11-12]、地理国情监测[13]、遥感[14-15]、导航[16]、无人机[17]等.并且由于GeoSOT剖分参考框架的科学性与实用性,相关部分成果已在国内高分专项、北斗专项等重大项目应用,并正在形成国防及公安、民政、新型智慧城市等重要行业部门的国家应用标准及草案.
GeoSOT网格剖分以国家大地坐标系CGCS2000为空间基准;沿用大地测量理论与技术体系,能够最大限度地继承现有历史空间数据;包含现有不同网格体系公共的4°、2°、1°、2′、1′、2″、1″、0.5″八个基本网格;能够聚合生成现有主要基于经纬度的标准网格.其剖分方案如下:
通过三次地球扩展(将地球表面真实空间扩展为512°X512°、将1°扩展为64′、将1′扩展为64″)实现整度、整分的四叉树划分,从而形成一个上至全球(0级)、下至厘米级边长(32级)的多尺度网格体系[18],如图1所示.
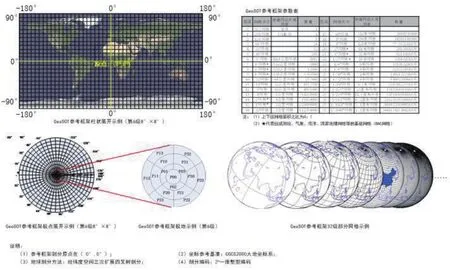
图1 GeoSOT地球剖分参考框架[9]Fig.1 GeoSOT reference frame
在GeoSOT格网划分的基础上,按照"Z"序为每个格网赋予层次性编码,编码形式主要有四进制一维数组(如图2所示)、二进制一维数组(四进制编码的二进制形式)和二进制二维数组(二进制一维数组的交叉分组)3种,均由度级、分级、秒及秒小数三部分组成.例如,四进制一维形式的编码12,其二进制一维形式的编码为0110,二进制二维形式的编码为(01,10).

图2 GeoSOT格网编码示意图[9]Fig.2 GeoSOT coding rule
2 基于GeoSOT的地表区域面积计算方法
2.1 计算原理
本文基于构建全球网格弧长数据库的思路提出一种新的计算方法,构建全球网格弧长数据库,采用预先计算、查表求和的方式,取代网格转换为经纬度范围再进行积分的计算方式,以期获得更高的计算效率.方案如下:
首先,采用数学方法计算基层级每一网格的边长.基层级需在19级4″及以下层级选定,以确保不包含不规则层级.随后,根据网格扩展方法,设计数据查找规则.对于输入的网格编码,确定其对应的数据块,进行求和操作,计算网格的面积,流程如图3所示.

图3 流程图Fig.3 Flow chart
2.2 经纬线弧长计算
经纬线弧长的计算方法可以根据几何方法求解[17].在地球椭球面上,纬线是圆.在任意一条纬线φ上求两点之间经差为μ的纬线弧长,可以利用下式:

地球椭球面上,经线圈是椭圆,曲率半径随着纬度变化.求两条纬线φ1φ2之间经线长度,需要进行积分,公式如下:

两式中,ae表示地球椭球赤道半径,e1表示第一偏心率.按照公式可以精确计算经纬度弧长.
GeoSOT采用CGCS2000大地坐标系,因此,本文地球椭球参数采用此大地基准给出的相关参数,与GeoSOT保持一致.CGCS2000大地基准中,ae=6 378137 m,扁率f=1/298.257 222101 ,利用扁率计算第一偏心率,公式为:

在计算中,取e12=0.006694380022 901.
GeoSOT进行经纬度划分时,在南北纬度88°以内采用四等分,在南北极处采用不同的划分策略.考虑到对称性,本研究只进行北纬0°~88°的计算,南半球的数据与北半球相同.
2.3 弧长查询方法设计
GeoSOT网格上至全球,下至1/2 048″,共分为32个层级,每一层级的网格经纬度跨度类似但不尽相同,主要原因在于GeoSOT的第二次和第三次扩展.在第9级向第10级划分时,首先将1°网格扩展到64′,随后再进行划分.1°网格向下划分到第10级,得到的4个网格跨度分别是32′X32′,32′X28′,28′X32′以及28′X28′,如图4a所示.对这4个网格进一步划分,将得到16个11级网格,其中16′X16′的9个,16′X12′的3个,12′X16′的3个,12′X12′的1个.进一步划分将得到64个网格,其中大部分是规则的8′网格,但仍有不规则网格,直到再下一次划分,才得到统一的共计225个4′网格.

图4 不规则网格的产生Fig.4 Irregular grids generation
在1′网格向下划分时,会出现相似的过程.不规则网格的出现给网格面积计算带来了困难.如28′X28′的网格与32′X32′网格层级一致,但面积比其小约1/4.
由球面对称性,可仅计算北纬0°~88°、东经0°~1°的单位纬线、经线长度,其余由旋转对称性和轴对称性可以求得.为方便计算,采用第22层级1/4″网格作为最小跨度,原因如下:1/4″网格精确度到米级,可以满足较高精度的使用需求;并且,1/4″网格精度高于由于扩展而产生的不规则网格的最小尺度,不存在残缺的网格,在进行更为细小的划分时,只需将长度进行均分即可.使用Matlab,根据式(2)以22层级网格1/4″为跨度进行积分,将结果保存数组中.数组的每一项表示北纬0°~88°,每条1/4″经线的长度,共有4X60X60X88=1 267200项.随后对其进行如下变换.
对第一个数组各项进行求和,可以得到0°纬线和88°纬线之间经线段的长度.将其变换为(4X60)X(60X88)的矩阵,则此时矩阵的每一列之和代表1矩经线段的长度.在这一矩阵下邻接一个(4X4)X(60X88)的0矩阵,更新为(4X64)X(60X88)的新矩阵,每列之和仍代表1°经线段的长度,但行数由4X60变到了4X64.对其进行一次划分,得到(4X32)的两个矩阵,第一个矩阵每一项都为正数,而第二个矩阵的最后4X4行都由0组成.这样的一次矩阵变换实现了1°向64′扩展操作在经线方向上的投影.
将矩阵邻接之后得到的(4X64)X(60X88)矩阵变换为(4X64X60)X88的新矩阵,则矩阵的每一列之和代表1°经线的长度,88列代表共88条1°经线.在其下方邻接(4X64X4)X88的0矩阵,则同上一次矩阵邻接操作类似,实现了1′向64″扩展操作在经线方向上的投影.最后,把矩阵整理为4X64X64X88项的一个向量,记为Lon,则向量Lon代表了从0°到88°的GeoSOT网格在经线方向上的投影.变换过程示意如图5所示.产生的结果向量_Lon、_Lat1以及_Lat2.随后,求取_Lon、_Lat1两个向量的内积,并数乘_Lat2向量的各项之和,结果即为该网格编码对应的地表面积.计算过程可以用下式表示:

对网格编码集中各面积进行求和,就可以得到所表示的地表区域面积.其中,由GeoSOT四进制编码求取对应划分的方法如下:设网格A的四进制一维编码Codei=a1a2…an,这里假设A在东北半球,因此,a1=1对于其他情况,由对称性可以方便求取.令i=2,3,…,n,对于ai%4=0或1,取Lon、Lat1的右区间,否则取左区间;对于ai%2=0,取Lat2左区间,否则取右区间,直到穷尽四进制一维编码的每一位,最终得到_Lon、_Lat1以及_Lat2.

图5 变换过程示意Fig.5 Matrix transformation process
3 实验结果与分析
经过矩阵变换,原来共计4X60X60X88项的数组,变换成为4X64X64X88的向量.任意一个1至22层级网格都能在向量Lon上找到一个区间来对应,区间包含的所有项之和构成该网格的经向长度.
纬向长度与经向长度略有不同.沿经线方向,不同纬度的同一跨度纬线段长度不相同,并且会受到扩展的影响;沿纬线方向,不同纬度的同一跨度纬线段长度相同,但也会受到扩展的影响.首先,沿经线方向计算不同纬度的同一跨度纬线段长.根据式(1),以1/4″为跨度进行计算,得到一个4X60X60X88项的数组.接下来的处理方法类似于经线长度,最终得到4X64X64X88项的一个向量,记为Lat1,代表0~88表纬线每隔1/4隔跨度的1/4隔纬线段长度.纬线方向的处理较为简单,不需要进行长度的实质计算.对于1线的跨度范围,构造一个4X60X60长度、各项为1的向量.随后,在向量的每隔4X60项插入4X4个0元素,并且在最后插入4X64X4个0元素,得到一个4X64X64的新向量,记为Lat2,其所有项由1和0组成.
在以上3个向量的基础上,以GeoSOT网格编码集表示的地表区域面积计算方法为:
对于网格编码集C中每一网格编码Codei,首先,根据网格编码,在向量Lon、Lat1和Lat2上找到对应划分所
根据文章第2部分所述的方法建立全球网格弧长数据库,数据文件总大小50 Mb左右.在此基础上,进行可行性实验及效率实验.实验环境:4 GB内存,Intel(R)Core(TM) i5-3230M 2.60GHz CPU,Win10 64-bit,软件环境为Matlab 2015b,实验过程及结果如下.
3.1 可行性实验与分析
可行性实验的主要思路是利用文中方法和传统借助经纬度的方法分别计算GeoSOT编码集代表的地表区域面积,对结果进行比较,通过相对误差大小来检验算法的可行性.
其中,经纬度法求地球表面规则区域面积方法的计算公式为:

式中,φ1、φ2代表始、终纬度,μ代表经度跨度.
采用随机数生成器,模拟生成东北半球不同层级的GeoSOT网格四进制一维编码,作为算法输入.实验进行500次,生成随机长度的四进制一维网格编码,使用两种方法分别进行计算并对结果进行比较.其中,无效网格编码78个.剩余422次结果的相对误差大多分布在±10-5之内,少量突破了10-5,但也在10-4以内.
实验结果表明,本文提出的计算方法在不同层级的计算中均能得到较准确的结果,计算相对误差在0.000 1以内.本文提出的基于GeoSOT的面积计算方法在不同层级的面积计算中具有可行性.
3.2 效率实验与分析
对于随机生成的东北半球的GeoSOT网格四进制一维编码,使用Matlab分别利用本文提出的方法以及积分方法进行多次计算,记录并比较程序总运行时间.实际测试时,每次进行2 000次面积计算,记录总用时.50次比较结果如图6所示,其中横轴表示实验次数,左纵轴表示运行时间,右纵轴表示经纬度积分方法与本文方法运行时间之比.

图6 时间记录Fig.6 Time record
实验结果显示,本文提出的方法在运行时间上优于传统方法,效率约为传统方法的7.5倍左右.传统方法使用复杂的积分进行面积计算.随着待求区域层级提高、面积变大,积分时间显著提高.本文提出的方法则采用事先计算的方案,从存储器中读出结果进行求和,使得计算效率大大提高.
4 结束语
本文提出了一种基于GeoSOT的区域面积计算方法,该算法以GeoSOT地球空间剖分参考网格为基础,根据GeoSOT剖分方案,设计编码查询规则,构建全球网格弧长数据库,根据编码查表计算网格面积.该方法基于全球剖分组织框架设计,具有全球统一性.通过应用实验,验证了该算法计算不同层级网格编码的可行性,并且相比传统方法,时间效率有大幅提高.该方法为地表空间面积计算提供了一种新思路.全球离散格网系统有望在大数据时代成为空间数据组织体系的标准框架,离散格网系统下的立体空间量算,是下一步研究中应重点考虑的问题.
