坑中坑式软土基坑抗隆起稳定性分析

，

(1.福建工程学院 土木工程学院，福建 福州 350118；2.福州大学 土木工程学院，福建 福州 350116)

随着我国基础设施建设的快速发展，高层建筑逐渐增多。为了满足施工和使用的需求，高层建筑存在着基础设备、电梯井和集水井等各种附属结构，导致在原基坑内进行二次开挖。坑中坑式基坑在我国逐渐变得非常常见，如位于上海浦东新区世博园的上海世博中心[1]，上海13号线下穿自然博物馆等[2]工程。坑中坑结构的施工造成被动区土体的卸载，导致基坑坑底的隆起增大，从而对基坑造成不利的影响。在进行基坑围护设计的过程低估内坑的影响造成的事故时有发生。目前对坑中坑的研究比较少，还不够深入。龚晓南[3]曾结合实际工程呼吁对坑中坑结构的重视。申明亮[4]对坑中坑结构进行参数化分析，提出了反映坑中坑几何特征的参数，并分析了参数对基坑应力场的影响。陈乐意[5]探讨了坑中坑计算深度的选取和坑中坑位置对基坑变形的影响。杨敏等[6]提出弹性支点法联合求解模型，用来解决坑中坑桩墙的内力变形计算。

基坑的稳定性分析包括整体稳定分析和坑底抗隆起稳定性分析两类。悬臂式支护结构往往发生整体失稳破坏，包括倾覆破坏和地基整体破坏，而带内支撑的基坑则易发生坑底隆起破坏。研究基坑抗隆起稳定性的方法有极限平衡法、极限分析法、数值分析法。强度折减有限元分析法是数值分析法中应用广泛的一种，最初由Zienkiewicz[7]和Ugar[8]提出，用于分析边坡稳定性问题。Cai[9]等将该方法应用于基坑坑底抗隆起稳定性分析。Goh[10]采用强度折减有限元法分析圆形基坑的抗隆起稳定性，提出一种计算基坑抗隆起稳定安全系数的简化公式。本文采用强度折减有限元分析法对坑中坑式基坑的抗隆起稳定性展开研究。

1 有限元模型

1.1 工程概况

某商住项目位于上海市奉贤区，该工程基坑分为两个区，A区周长约225 m，开挖面积3 300 m2，开挖深度9.15 m；B区周长约670 m，开挖面积约21 300 m2，开挖深度4.65 m。具体施工流程为先施工A区，再施工B区。A区基坑围护结构采用劲性水泥土搅拌桩法(SMW工法)，SMW工法型钢采用H700×300×13×24(插一跳一)，桩长20 m。设置两道混凝土支撑，第一道混凝土支撑截面尺寸800 mm×1 100 mm，位于-0.8 m处。第二道混凝土支撑混凝土支撑截面尺寸900 mm×800 mm，位于-4.8 m处。相邻内支撑水平间距7 m。内支撑混凝土采用C35，钢筋采用HPB300。基坑土体的物理力学参数如表1所示。各土层的物理力学性质参数根据室内土工试验及野外原位测试得到。

表1 土体物理力学参数

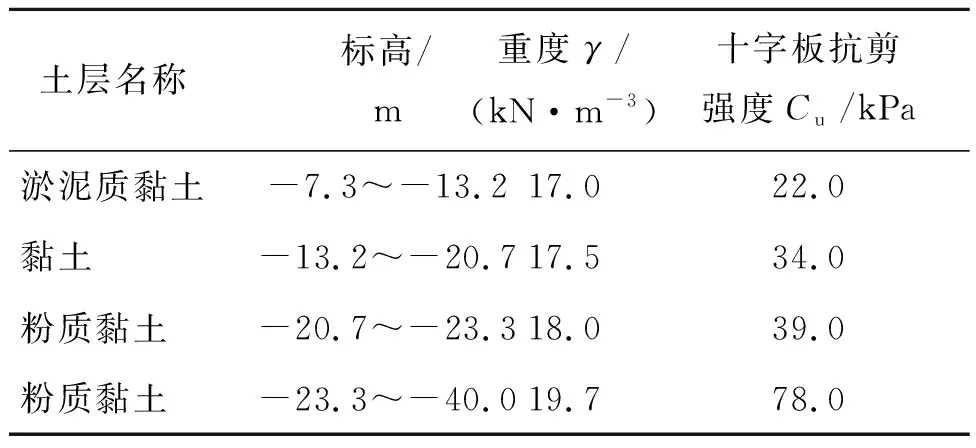
续表1

1.2 模型建立

该工程A区存在着大量的内坑，包括电梯井和集水井，对外坑的抗隆起稳定性有着不可忽视的影响。其中落深3.9 m的电梯井内坑尤其需要引起重视。采用强度折减有限元分析法选取该电梯井所在的一个基坑剖面进行二维平面稳定性分析。由于该工程中地基土为软黏土，并且只考虑短期工况，因此土体假定为不排水条件，采用总应力法进行分析。建立的基坑几何模型如图1所示，假定土体变形符合平面应变状态。数值模拟区域大小150 m×40 m，模型左侧添加水平位移约束，右侧添加水平位移约束，底部添加水平和竖向位移约束。外坑宽48.4m，挖深8.5 m。内坑宽7.0 m，挖深3.9 m。本文土体模型采用Mohr-Coulomb就能得到与实际接近的剪切破坏面。各层土体的物理力学性质指标采用表1中的值。泊松比ν=0.495，φ=0，不排水强度指标Su用现场的十字板抗剪强度Cu代替。不排水模量Eu根据经验取500Su。外坑围护结构采用水泥土搅拌桩内插型钢的方法，采用板单元模拟型钢，用实体单元模拟水泥土搅拌桩，水泥土搅拌桩同基坑土体采用Mohr-Coulomb模型进行模拟。外坑设的两道内支撑用连接件进行模拟。其各项物理力学指标如表2所示。内坑围护结构采用水泥土搅拌桩，水泥土采用模型和各向物理力学指标同外坑。水泥土与周围土体土体的接触面用剪切节理进行模拟，接触面的材料同周围土体，强度参数为相邻土体乘以折减系数0.8。地下水位位于-1 m，本文只考虑不排水工况，不考虑地下水的渗流耦合，仅把地下水视为静水压力进行计算，设置开挖面没渗流。

考虑到土体在不同应力路径下的变形和破坏的特征是不同的，本文先采用弹塑性分析模拟基坑开挖的施工过程。土层采用6-高斯节点单元模拟，单元数量2000，有限元网格如图2所示。开挖完成后再强度折减分析，单元类型采用上限单元，单元数量2000，并且采用网格自适应，3次自适应迭代，自适应控制变量为剪切耗散。网格自适应能够优化潜在破坏面附近的网格，避免局部破坏或屈服产生的剪切带。具体模拟过程：

1)计算初始应力；

2)分层挖至-1.3 m，施工第一道水平支撑；

3)分层挖至-5.3 m，施工第二道水平支撑；

4)分层挖至外坑坑底-8.5 m；

5)分层挖至内坑坑底；

6)进行强度折减分析。

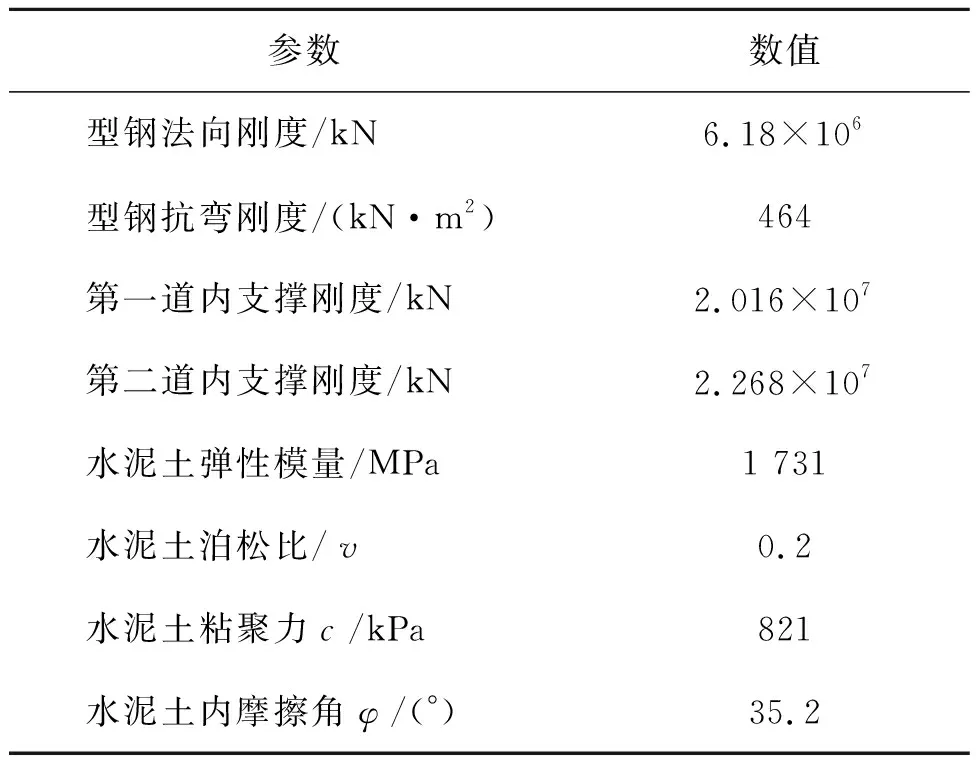
表2 支护结构物理力学参数

图3～6为各个开挖阶段弹塑性分析得到的等效塑性应变图，可以发现随着外坑开挖塑性应变区域在外坑支护结构底部发展。当内坑开挖后，内坑底部产生塑性应变区域。图7为强度折减得后得到的等效塑性应变图，可以发现内坑坑底的塑性应变区域与距离外坑较近一侧的塑性区域贯通，形成完整的剪切破坏面，剪切破坏面近似圆弧状，覆盖整个内外坑，并交汇于内坑坑底的某点。坑外土体沿着剪切破坏面发生塑性流动，最终导致隆起破坏。坑中坑式基坑抗隆起稳定安全系数的上限为1.07。坑底最大隆起值为10.00 cm发生在内坑坑底。因此在设计外坑支护条件时必须考虑内坑的影响。

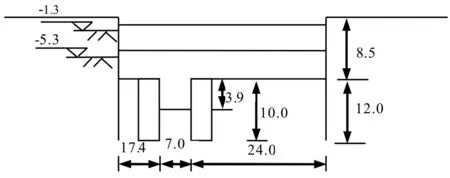
图1 坑中坑式基坑几何模型(单位：m)Fig. 1 Geometric model of the base pit of pit-in-pit (unit: m)

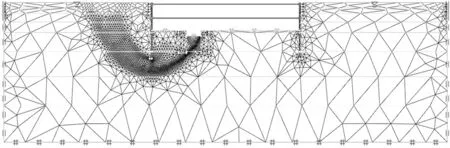
图2 强度折减阶段有限元网格模型示意图Fig.2 Finite element mesh model of the strength reduction phase

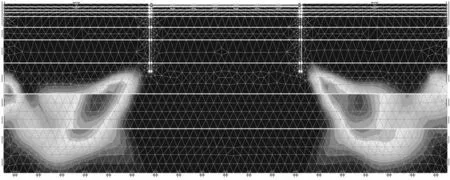
图3 第一层开挖塑性区域Fig.3 Plastic strain zone of the first excavation phase

图4 第二层开挖塑性区域Fig.4 Plastic strain zone of the second excavation phase

图5 第三层开挖塑性区域Fig.5 Plastic strain zone of the third excavation phase

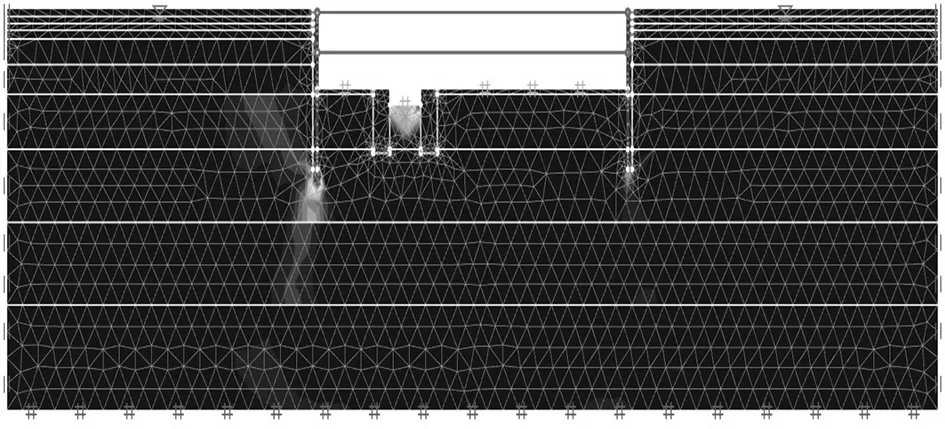
图6 内坑开挖塑性区域Fig.6 Plastic strain zone of the inner excavation phase

图7 有限元模拟得到的破坏面Fig.7 Failure surface based on FEM simulation

2 有限元参数分析

2.1 基坑抗隆起稳定分析

安全系数fs是判定基坑是否稳定的关键因素，当fs大于1时表示基坑处于稳定状态，当fs小于1表示基坑处于不稳定状态。有限元强度折减分析法是对基坑土体的黏聚力c和内摩擦角φ进行折减直到基坑不再稳定，得到新的c′和φ′。有限元强度折减分析中假定c和φ的折减不影响其他土体的性质，并且c和φ对于土体的抗剪强度同等重要。强度折减有限元分析能够自动生成基坑的剪切破坏面和安全系数，安全系数fs为

(1)

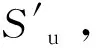
(2)

为了研究内坑的尺寸以及内外坑之间的距离对坑中坑式基坑抗隆起稳定性的影响，建立图8所示的几何模型。定义参数距离比α=d/D，其中，d为内外坑间距离；D为外坑宽度。内外坑深度比β=h/H，其中h为内坑的深度，H为外坑的深度。内外坑的宽度比R=b/D，其中b为内坑的宽度，D为外坑的宽度。

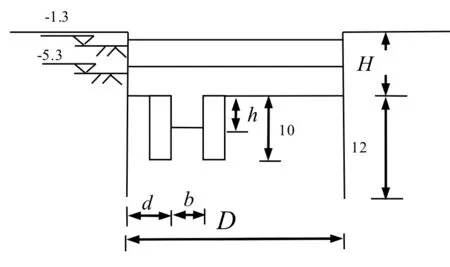
图8 参数分析坑中坑几何模型(单位：m)Fig.8 Geometric model of pit-in-pit’sparameter analysis (unit: m)

2.2 距离比影响

为了研究内外坑间距离对坑中坑式基坑抗隆起稳定性的影响，保持基坑的各项几何参数不变，取R=0.08，β=0.2，改变距离比α分别取0.13、0.21、0.29、0.43、0.56进行分析。

强度折减得到的剪切破坏面通过贯通的塑性应变区确定，图9为内外坑距离比α分别取0.13、0.29、0.56的等效塑性应变图，其中虚线为人为添加的破坏面。可以发现内外坑之间的距离会影响坑中坑式基坑的破坏面形式。当内外坑的距离比α<α0时(α0为0.21～0.29)，破坏面的形式为单一的整体破坏面，破坏面同时覆盖整个内外坑。此时需要考虑沿着整体破坏面的抗隆起稳定性。当内外坑的距离比α=α0，除了整体破坏面，在外坑的挡墙处会形成单独外坑破坏面，此时需要同时考虑沿着外坑单独破坏面的稳定性和沿着整体破坏面的稳定性。当内外坑的距离比α>α0，只存在外坑单独破坏面，此时只需要考虑沿着外坑破坏面的稳定性。

图10为不同内外坑距离比下的坑中坑式基坑抗隆起稳定性安全系数。从图中可以发现抗隆起稳定安全系数与内外坑距离比成正相关。内外坑间的间距越大，基坑抗隆起稳定性越强。

2.3 深度比影响

为了研究内坑深度对坑中坑式基坑抗隆起稳定性的影响，保持坑中坑式基坑的各项几何参数不变，取R=0.12，α=0.43，改变内外坑深度比β分别取0.1、0.2、0.3、0.4进行分析。

图9 不同内外坑间距下的等效塑性应变图Fig.9 Equivalent plastic strain with different spacing of inner and outer pits

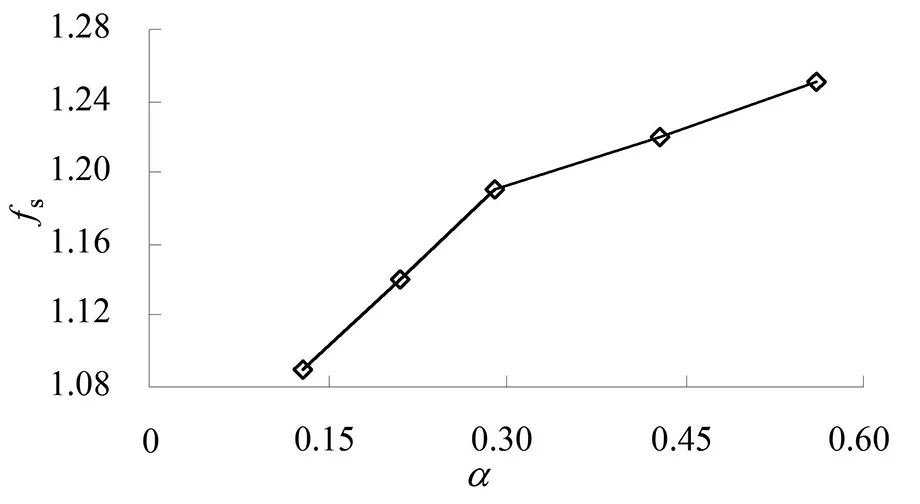
图10 不同间距比对安全系数的影响Fig.10 Effects of different spacing ratios α on the safety factor

强度折减得到的破坏面通过贯通的塑性应变区确定，图11为深度比取0.1、0.2、0.4得到的等效塑性应变图。可以发现深度比β对破坏面的形式有影响。当深度比β<β0(β0为0.2～0.3)，只存在外坑单独的破坏面，此时只需要考虑沿着外坑破坏面的稳定性。当深度比β=β0，外坑破坏面和整体破坏面同时存在，此时需要同时考虑沿着外坑单独破坏面的稳定性和沿着整体破坏面的稳定性。当深度比β>β0，只存在整体破坏面，此时只需要考虑沿着整体破坏面的抗隆起稳定性。

图12为不同内外坑深度比下的坑中坑式基坑抗隆起稳定性安全系数。从图中可以发现抗隆起稳定安全系数与内外坑深度比成负相关。内坑深度越大，基坑抗隆起稳定性越差。

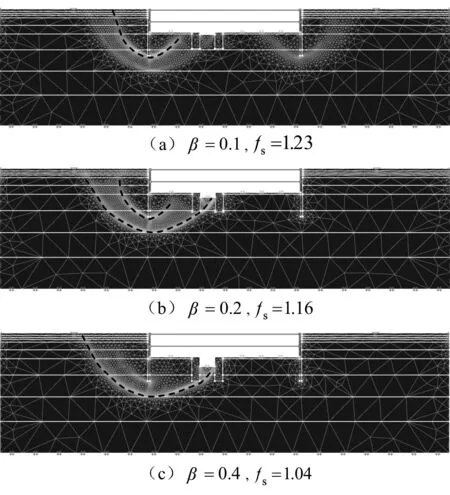
图11 不同内坑深度下的等效塑性应变图Fig.11 Equivalent plastic strain with different depths of inner pits

图12 不同深度比对安全系数的影响Fig.12 Effects of different depth rations β on the safety factor

2.4 宽度比影响

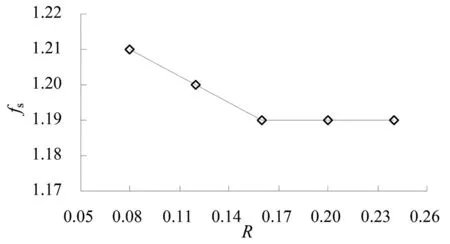
为了研究内坑宽度对坑中坑式基坑抗隆起稳定性的影响，保持坑中坑式基坑的各项几何参数不变，取α=0.43，β=0.2，改变内外坑宽度比R分别取0.08、0.12、0.16、0.20、0.24进行分析。

强度折减得到的破坏面通过贯通的塑性应变区确定，图13为宽度比取0.08、0.12、0.24得到的等效塑性应变图。可以发现宽度比R对破坏面的形式有影响。当深度比R

图13 不同内坑宽度下的等效塑性应变图Fig.13 Equivalent plastic strain with different widths of inner pits

图14为不同内外坑宽度比下的坑中坑式基坑抗隆起稳定性安全系数。从图中可以发现抗隆起稳定安全系数与内外坑宽度比成负相关。内坑宽度越大，基坑抗隆起稳定性越差。当β≥0.16安全系数不再发生变化，继续增大内坑宽度对基坑的抗隆起稳定性没有影响。

图14 不同宽度比对安全系数的影响Fig.14 Effects of different width ratios R on th safety factor

3 结论

1)坑中坑式基坑中内坑开挖对外坑抗隆起稳定性分析有着不容忽视的影响，由于内坑开挖使得内坑底部产生塑性应变区，使原本单一基坑的破坏面发生改变。

2)坑中坑结构抗隆起破坏面近似圆弧形，覆盖整个内外坑，穿过外坑挡墙，并与内坑坑底交汇于某点。坑外土沿着破坏面向内坑发生塑性流动，导致最大隆起发生在内坑坑底。

3)坑中坑式基坑隆起破坏面的形式与内外坑的间距比、内外坑的深度比和宽度比相关，根据内外坑间距比临界值α0、内外坑深度比临界值β0和内外坑宽度比临界值R0划分成不同的破坏面形式：第一，当α<α0，只存在内外坑的整体破坏面；当α=α0，整体破坏面和外坑的单独破坏面同时存在；当α>α0，只存在外坑单独的破坏面。第二，当β<β0，只存在外坑的单独破坏面；当β=β0，整体破坏面和外坑的单独破坏面同时存在；当β>β0，只存在内外坑的整体破坏面。第三，当R

4)坑中坑式基坑的抗隆起稳定安全系数与内外坑间距比α成正相关，与深度比β和宽度比R成负相关。