基于改进Excel-AHP模型下的初始水量分配
2018-10-16徐江申王立权
徐江申,王立权
(黑龙江大学 水利电力学院,哈尔滨 150080)
1 概 述
对于初始水权水量的分配,考虑到多目标多决策问题,很难单一的从主观上和客观上对水量进行如何分配。根据之前我国以经济效益为首位这一国情的特点,随之而来的是水污染问题的持续恶化,则需将生态影响纳入其中考虑,甚至在自然保护区,是重点优先因素。AHP法则是将人的主观因素和客观因素综合考虑,避免单一主观因素的人为性,单一客观因素的机械性,即综合考量具有更好的科学性和说服力。AHP解决问题的思路是:首先根据问题的具体情况和要求,把需要解决的问题层次化,依照性质及需要达到的目标将问题分解为不同的组成因子,按因子间的相互影响及隶属度关系将各层次各因素聚类组合。
2 模型介绍
2.1 层次分析法Excel法的理论基础
层次分析法Excel法利用电子表格具有较强的存储性、计算性、系统性,利用函数运算、编辑公式,自动计算以及单元格等式的引用,省略了再次输入的重复性,这就使得判断矩阵每个因子之间具有很好的关联性,改变一个因子就会得到不同的结果。
2.2 AHP(层次分析法)的基本步骤
运用AHP方法解决决策问题,主要按以下步骤操作:①将复杂的问题分解,利用Microsoft Office Visio或者WPS建立层次结构流程图;②结合主观和客观分析,构造两两判断矩阵;③结合Excel和判断矩阵计算比较元素的相对权重;④计算每层元素的综合权重[1]。
在进行判断矩阵构造时,所依据的是1~9比例标度。例当aij=3时,也就是一个因子相对另一个因子显得稍微重要(表1),将得到的综合权重,按从大到小的顺序进行排列,就很容易知道哪个方案孰重孰轻。

表1 相对比例标度
3 层次分析法的优缺点
3.1 层次分析法存在的问题
第一:不能提供新方案,只有从备选方案中选择最优选项,通过对已有方案的筛选绝大部分是依靠人为主观因素,没有通过实践的证明。此外,在备选方案中只能初略了解各方案的重要性,也就是模糊的定量评价,不清楚各方案存在的优点和缺点及能解决的问题。如果将此方案推行不一定效果好于实施方案,同时不能对现状实行综合评价,这大大增加一个方案替代另一个方案的因素不确定性。第二:定量成分少,说服力不够充分,科学方案的评估是结合数学论证和定量评价。层次分析法是人脑主观意向的一种反映,不同的决策者在作出决定时往往会有不一样的结果,缺少支持自己观点的数学理论推导。第三:多指标体系,统计量大,且确定权重困难。当我们想用层次分析法解决普通问题时,由系统结构理论知需要弄清楚关系环,也就是基础层次与上一层次之间的关系,对关系的掌握程度越高,则判断矩阵的阶数增加,两两指标的重要性就更加难以确定,甚至对层次单位排和层次总位排产生影响。构造判断矩阵后,一致性检验通过。
3.2 改进的层次分析法的优点
在构造判断矩阵时多数情况下,矩阵的一致性不在合理范围内,而改进的层次分析法最大的优点就是通过一致性简洁,这种情况尤其在矩阵阶数不是很高时体现的尤为明显,与案例结果关联程度高,较容易获得满意的实施方案。在一致性比率越接近零时,可认为判断矩阵的可靠性越强,其最大的优势在于在合理区间进行再调整;其次大大简化了计算复杂程度,本法对数阶矩阵进行计算的结果和Matlab相比较,其计算结果吻合;而且环环相扣,相同的单元格式可以调用,同时采用方根法时可以用power函数,及列行累加累乘;最后,每行列所得的结果是存储式,下面列表数据,为了美观只显示4位小数,因此没有进行四舍五入,通过环环减少误差,使所得计算成果精度更精准。另外采用广泛的办公平台软件,对技术人员的要求低,没有具体的专业术语,适合大部分研究人员和学者的操作。
4 案例计算
将改进的AHP法运用到哈尔滨市某县初始水量分配案例上。首先建立水量分配指标体系,初始水量分配在农业、工业、生态等行业中起着举足轻重的作用,同时在指标体系选择过程中,应充分考指标的代表性、关联性、可靠性,在数据处理中容易量化、简洁,可操作性强等因素。通过上述原则,本文一共选择4个指标:经济效益、生态效益、社会效益、技术要求。层次结构图见图1。
由文献可知[2],1~10指标一致性指标见表2。
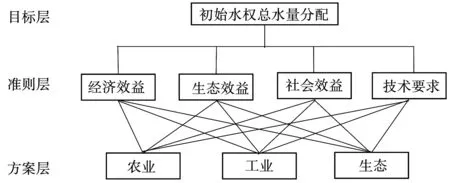
图1 层次结构图

n12345678910RI000.580.891.121.261.361.411.461.49
本文选定n=3,RI=0.58;n=4,RI=0.89的指标纳入计算。求判断矩阵特征值和特征向量时,可以用以下3种计算方法,分别是和法、幂法、方根法。用A代表技术要求;B代表生态效益;C代表经济效益;D代表社会效益;E代表累积相乘;F代表采用方根法。经过改进的层次分析法,得到准则层和方案层对于目标层的判断矩阵、权重及最大特征值,特征向量的计算结果见表3、表4。
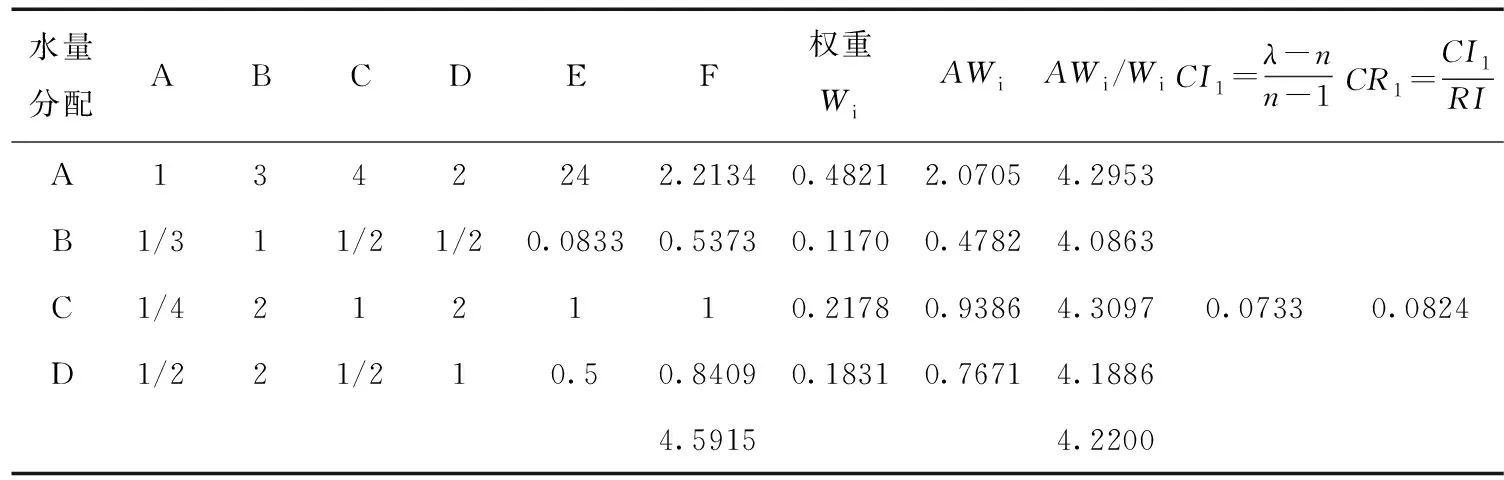
表3 准则层对于目标层的判断矩阵及单排序和一致性检验
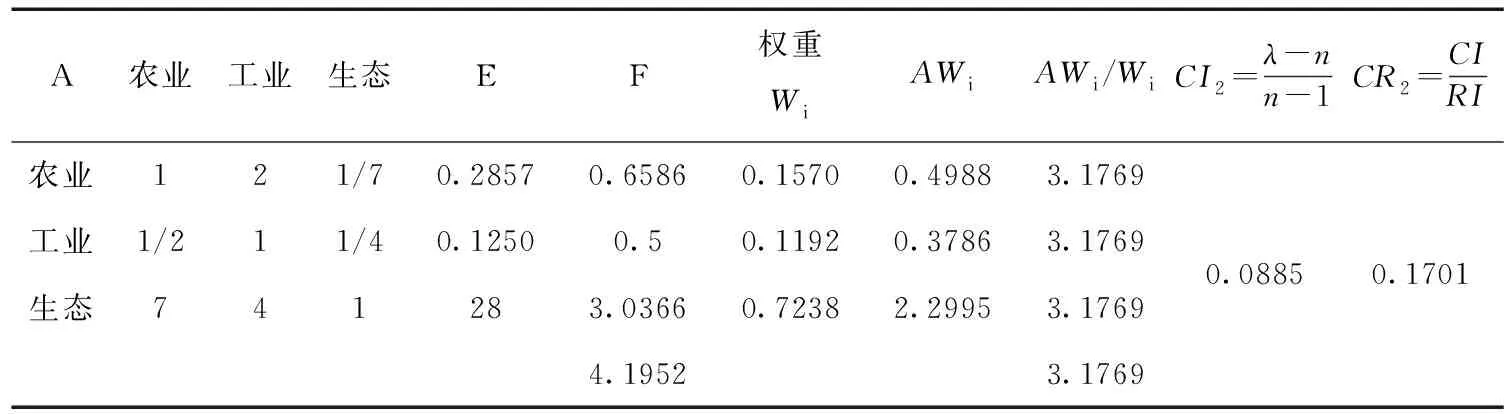
表4 方案层对技术要求准则的判断矩阵及单排序一致性检验
通过方案层对技术要求准则判断矩阵的一致性列表可知,一致性比率为0.1701明显大于要求的0.1这一标准,故此判断矩阵需要进行一致性调整。见表5-表7。
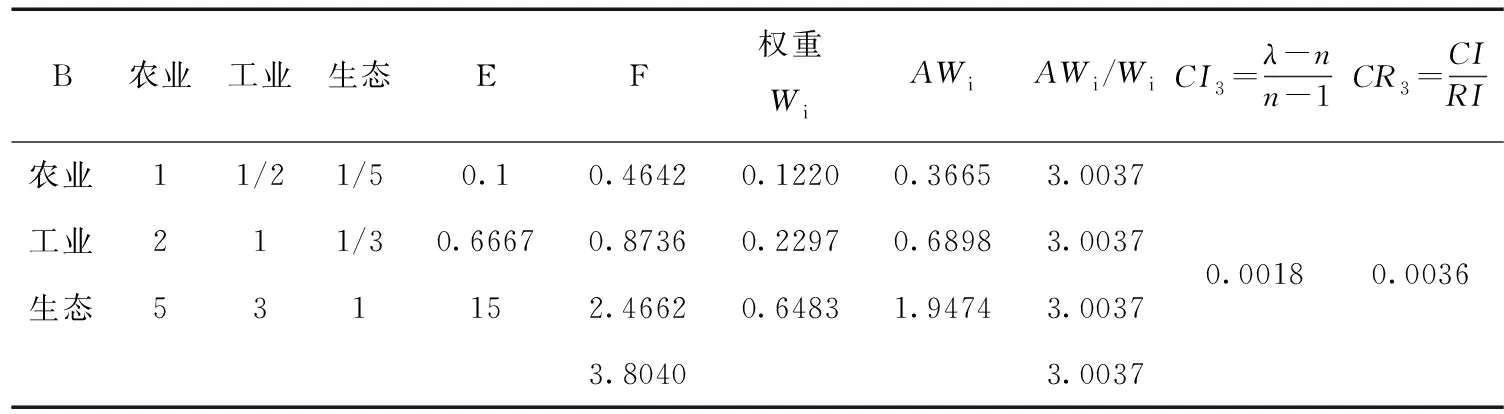
表5 方案层对于生态效益准则的判断矩阵及单排序一致性检验
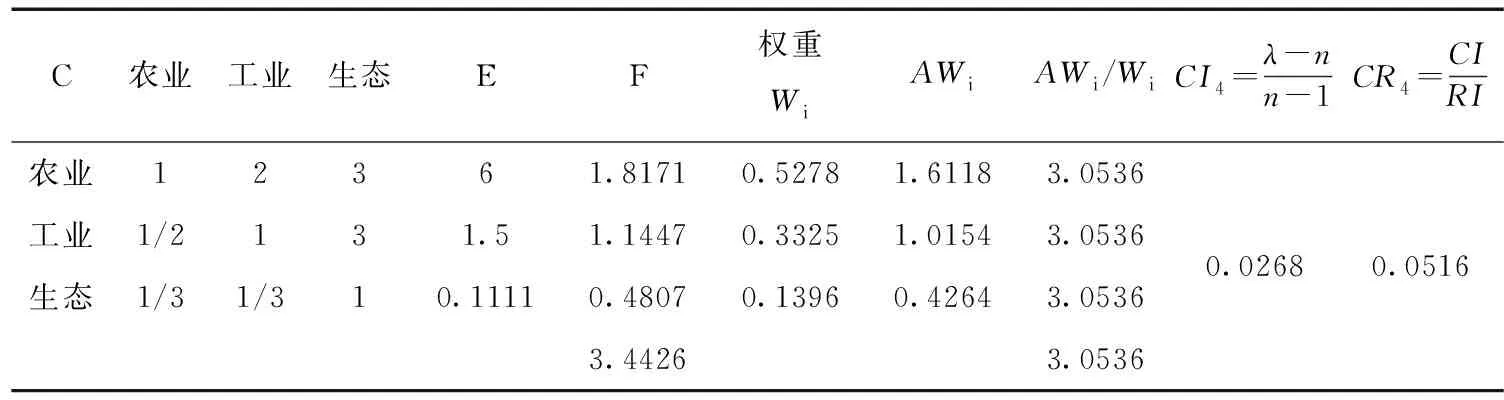
表6 方案层对于经济效益准则的判断矩阵及单排序一致性检验
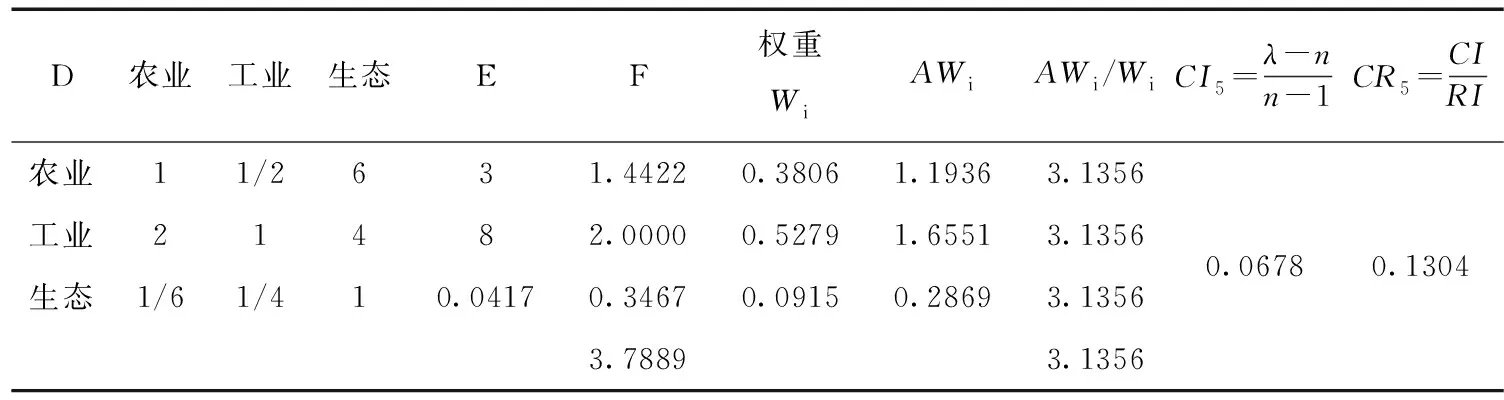
表7 方案层对于社会效益准则的判断矩阵及单排序一致性检验
通过计算结果不难发现,方案层对技术要求准则的判断矩阵和方案层对于社会效益准则的判断矩阵的一致性比率即CR5>0.1,故一致性未通过。经改进的AHP法调整,将方案层对技术要求准则的判断矩阵中的指标a12、a13、a32分别调整为1/5、1/9、1/2。上三角是通过公式aij=1/aji,并通过储存关联,知a21、a31、a23自动调整为5、9、2。相应的,方案层对于社会效益准则的判断矩阵只调整了a12=1/2,得到结果见表8-表9。
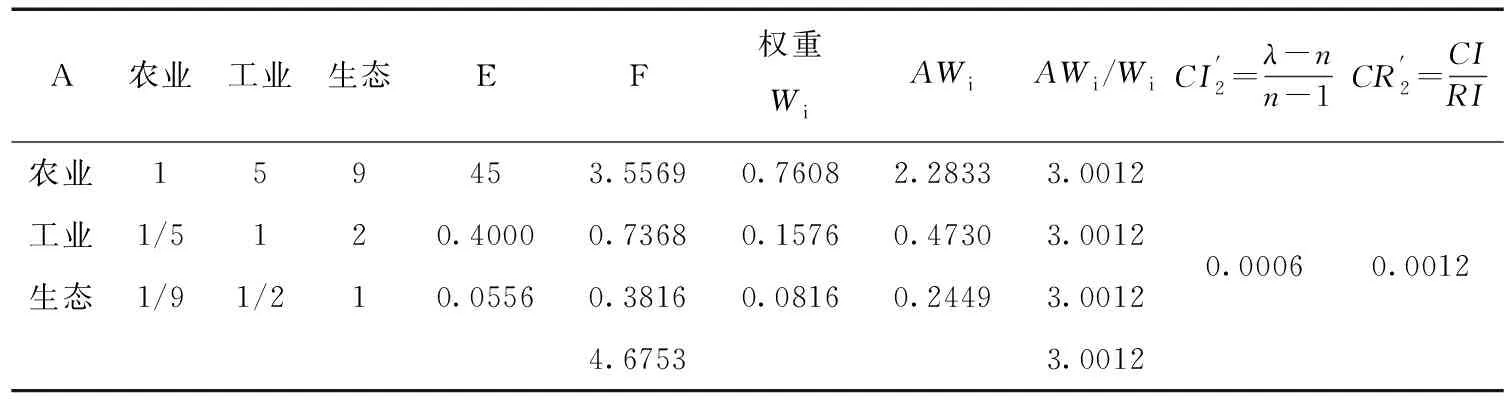
表8 方案层对技术要求准则的判断矩阵及单排序一致性检验
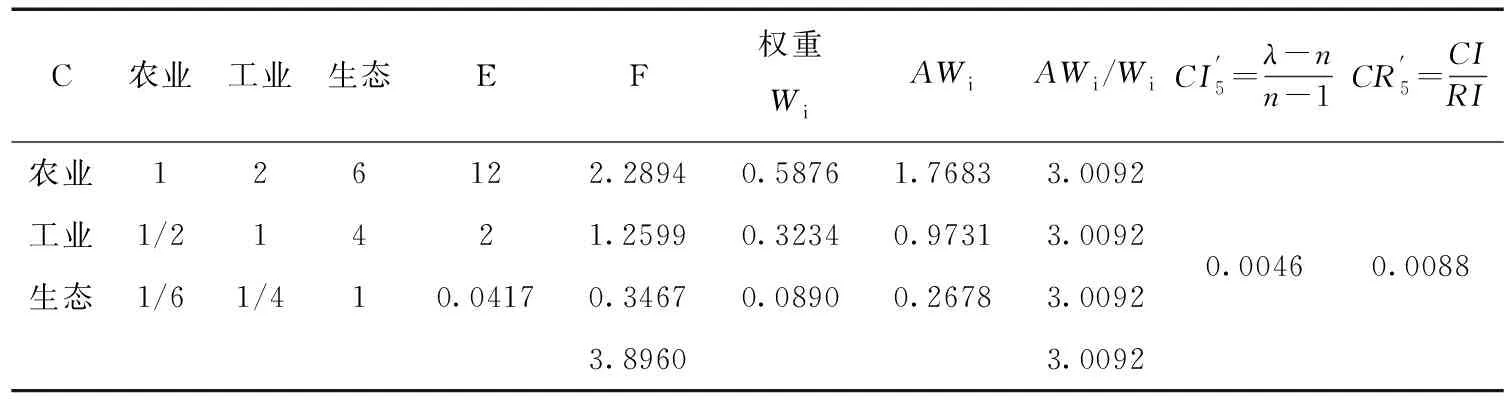
表9 方案层对于社会效益准则的判断矩阵及单排序一致性检验
经过一系列调整,从随机的一致性通过率来看,为60%,调整后的一致性皆符合限制条件,故层次总排序见表10。
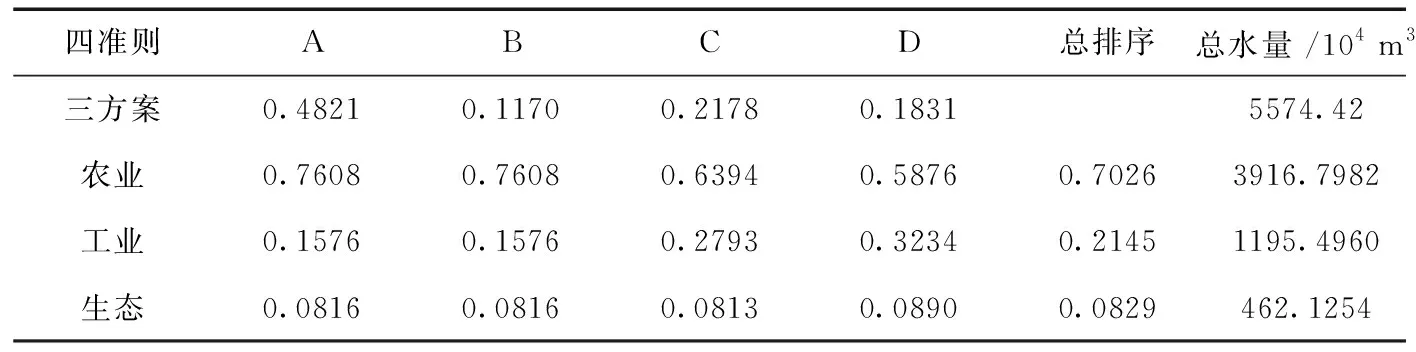
表10 层次总排序计算
通过改进的AHP法,调整判断矩阵从一致性前后调整图很明显看出经过调整后的一致性比率比原始计算结果小,相比较一致性检验已合格的数据,其约束条件更苛刻,故合理性更好。一致性比率前后调整图见图2。
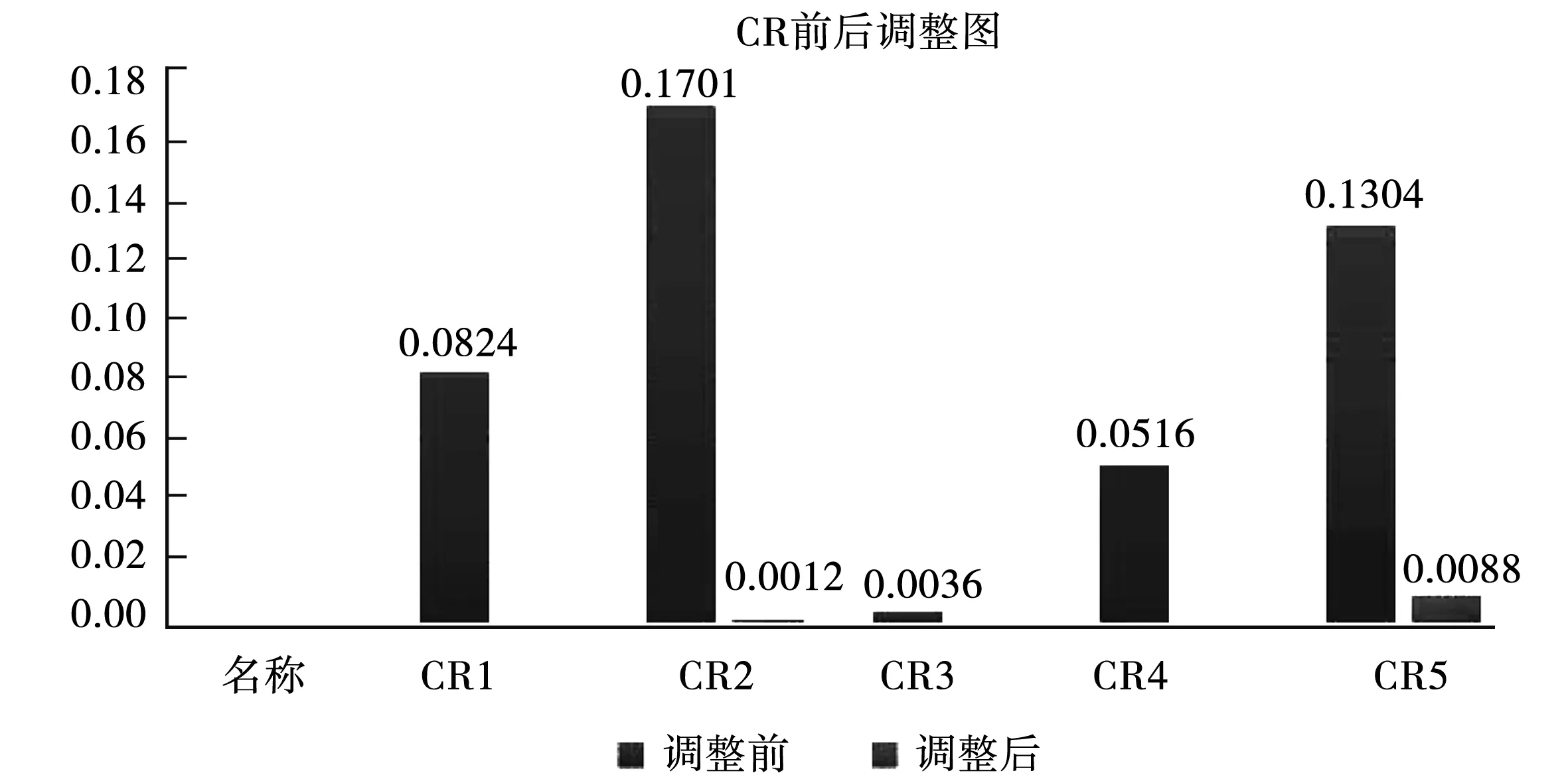
图2 一致性比率前后调整图
以某县初始水量分配为例。根据用水总目标的5%计算,确定预留水量[4],故工业、农业、生态总分配水量为5 574.42×104m3。由表10可知(保留两位小数),农业分配水量为3 916.80×104m3,工业分配水量为1 195.50×104m3,生态分配水量为462.13×104m3。
5 结 语
改进的层次分析法在初始水量分配上有很好的灵活性,相对于传统的层次分析法而言,可以调整参数中的任意影响因子,其优势主要如下:让判断矩阵一致性通过变得轻而易举;在一致性允许范围内,进一步缩小一致性值,这是层次分析法做不到的;能直观看出各用水行业的权重,进而得出各行业水量分配结果,从现状用水情况来看,水量分配更合理。
