检验双重性质特征的基因模糊聚类分析方法
2018-10-16祖颖,朱平,马冲
祖 颖,朱 平,马 冲
江南大学 理学院,江苏 无锡 214122
1 引言
序列比较是计算生物学中最重要的任务之一,通过它可以判断生物序列之间的差异或相似性。此外,准确估计生物序列之间的相似性可以很好地应用于相似性分析[1-2]、系统发育分析[3-4]等。基于比对的方法是序列比较中使用的主要方法,如Smith-Waterman算法[5]和BLAST[6],这些方法通常通过动态规划原理得到最佳对齐结果[7]。然而,这些基于比对的方法在应用中存在一些缺点[8]。首先,在利用比对的方法进行序列对比时,序列必须在可靠对齐的前提下才能获得良好的结果。由于一些序列发生了基因序列重排,如基因重组或水平基因转移,所以难以获得准确地结果。其次,随着低成本高通量测序技术的普及,更多完整的基因组和更多的数据可被利用。因此,利用比对的方法进行序列对比是非常耗时的。
结合上述分析,在基于比对的方法之外,也产生了很多不基于比对的方法和应用。其中K字词频率的方法大多数被应用在快速对序列进行物种分类的方面。最常见的基于K字词频率和Markov链模型的方法包括欧氏距离测量[9]、夹角余弦值测量[10]、标准化欧氏距离测量[9]。Kun等[11]在Torney等[12]、Reinert等[13]和Wan等[14]提出的和统计学方法基础上重新加权定义,并取得了更准确的聚类结果。基因序列某些片段的重要性在序列对比中存在着差异。当一些片段的顺序和频率几乎保持不变时,可以合理地假设这些片段对区分序列几乎没有作用。如果序列片段的顺序和频率有很大的差异,应该假设这些片段对于区分序列有很大的作用。基于上述分析,通过利用重新加权定义的统计学方法,并将其应用于基因序列聚类能够获得更准确的结果。
核酸碱基对的相互作用是生物结构中的重要作用[15],DNA结构也通过链内碱基对相互作用来维持。它在DNA序列的稳定性中起着至关重要的作用。GC碱基对的平均堆叠相互作用比AT碱基对强两到三倍[16],与将双链DNA序列保持在一起的其他相互作用(氢键和疏水相互作用)相比,DNA序列中碱基对相互作用的能量明显较大,因此在计算序列之间的距离时,碱基对的相互作用应该被考虑进去。
在本文中,将4个碱基(A,T,G,C)之间的二阶马尔可夫模型等价于具有16个二核苷酸状态的一阶马尔可夫链模型,通过计算AA,AT,AG,AC,TA,TT,TG,TC,GA,GT,GG,GC,CA,CT,CG和CC之间的转移概率,同时引入核酸碱基对的相互作用,将它作为一组权重值,通过模糊聚类分析检验双重性质特征的合理性,并利用欧氏距离和夹角余弦值距离这两种统计学方法对比单一性质和双重性质方法的准确性。实验结果表明双重性质方法更加准确。
2 方法
2.1 Markov链模型
基于Markov链模型的转移概率矩阵,一种直接用特征矩阵来刻画基因序列的方法,具体描述如下。
对于一个给定的长为n的基因序列s=s1s2…sn,基因序列X(s)Markov链模型的转移概率矩阵(Sij代表状态ij的个数,Si代表状态i的个数),即由状态i转移到状态 j的概率,因为碱基有4种,那么就有4个可能的状态,所以a[i][j]共有4×4种可能的取值。把它们用矩阵表示成:

2.2 核酸碱基对的相互作用
多属性决策是指在考虑多个属性的情况下,选择最优备选方案或进行方案排序的决策问题。如果第 j个属性的值在所有决策中变化很小,认为这个属性对决策做出了小的贡献,应该给予一个小的权重。相反,如果第 j个属性在所有决策中明显不同,这个属性被认为在做出最佳决策中发挥重要作用,应该给予很大的重视。在本文中,当一个二核苷酸在序列对比作出的贡献很小时,应该分配较小的权重,当一个二核苷酸在序列比对中贡献很大时,应该分配较大的权重。由于每个二核苷酸具有不同的重要性,考虑核酸碱基对的相互作用作为一组权重值,再构造具有双重性质的特征矩阵,并用模糊聚类分析来检验该方法的合理性。
基于上述分析,本文考虑核苷酸两个性质:一个是基于碱基之间的转移概率;另一个是核酸碱基对的相互作用。对于第二个性质,在Markov链模型的转移概率矩阵中引入核酸碱基对的相互作用,同时定义相互作用[17]:
相互作用=核酸碱基对的相互作用×碱基转移概率
核苷酸之间相互作用的3个概率[17]如下:嘌呤(A,G)转换嘧啶(C,T)概率是1/2,反之亦然;嘌呤转换嘌呤或者嘧啶转换嘧啶的概率是1/3;相同的核苷酸转换的概率是1/6。这种概率的假设是根据在物种的进化的过程中生物效应的转换。
例如从数据库找出一个物种的基因序列片段:
S=AGGCGTTACTGCCTAA
通过Markov链模型计算出该序列对应的转移概率矩阵为MM,核苷酸相互概率矩阵为MI:
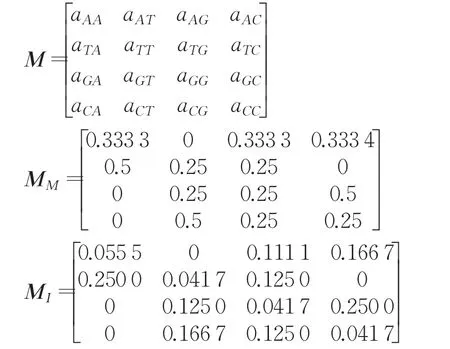
因此,表1中的每个基因序列都可以通过计算得到上述两种矩阵,使用适当的方法计算两序列之间的距离矩阵。本文使用欧氏距离d(A ,B)[18],定义如下:
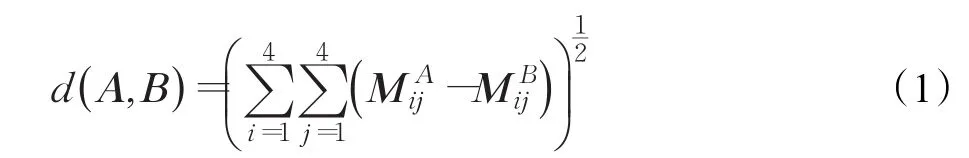
考虑两个特征来计算序列之间的距离。那么序列A和B之间总的相似性dT(A ,B)[19]定义为:
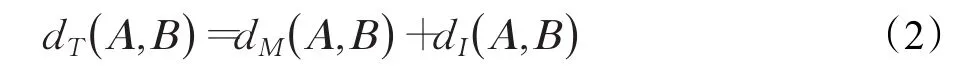
其中,dM(A,B)表示是碱基的转移概率的相似性,dI(A,B)是碱基的相互作用的相似性。
通过上述距离矩阵,得到16个物种的动态模糊聚类图,从而检验双重性质方法的合理性,并根据不同的统计学方法比较单一性质和双重性质方法得到的分层聚类结果。
3 16个物种的p53基因序列的欧氏距离矩阵
从NCBI数据库里选取了鼢鼠、普通牛、人类等16个物种p53基因完整的CDS序列,来源及序列号见表1。
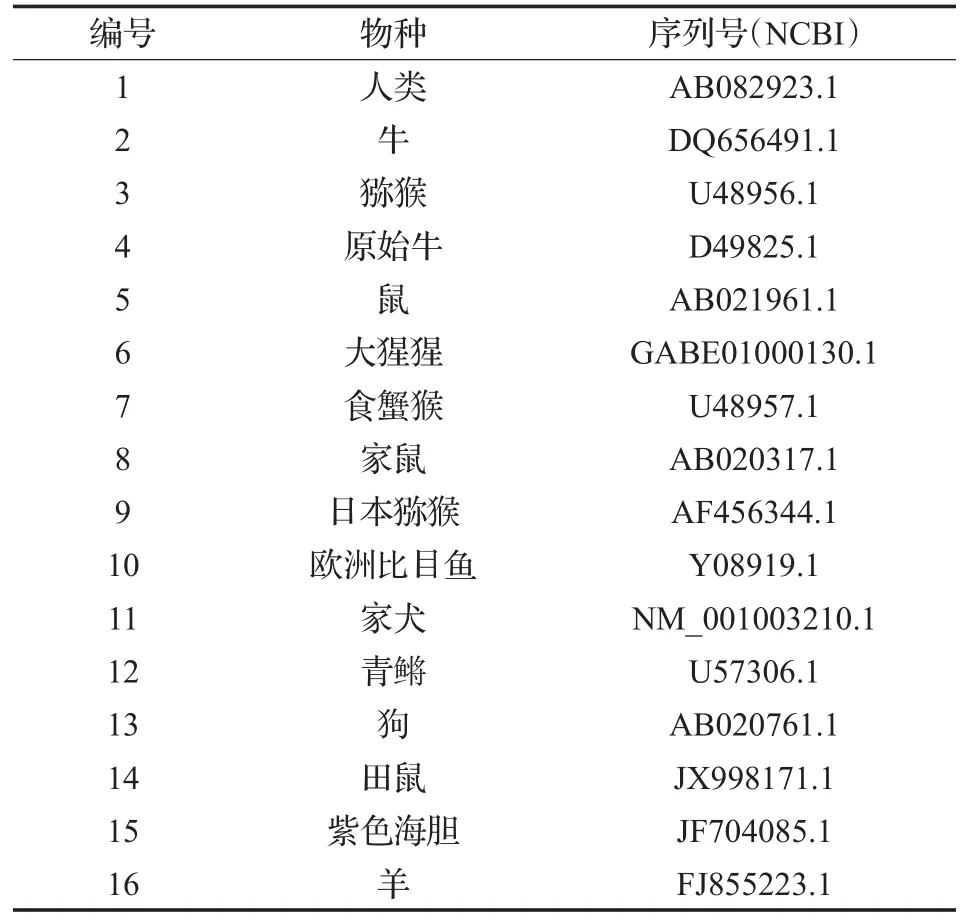
表1 16条p53基因完整的CDS序列的物种来源及序列号
基于上述的方法,通过Matlab计算表1中所有序列的4×4矩阵 MM和 MI,根据公式(1)和公式(2)计算序列之间的欧氏距离。利用计算得到的欧氏距离来分析16个物种的p53基因序列的关系,从而来检验双重性质特征方法的有效性。
4 模糊聚类
4.1 相似度计算
基因序列越相似,它们之间的特征值就越小。基于距离方法两样本之间关系的度量时统计学中通常用的做法是,为了进一步构造模糊邻近关系矩阵,刻画各个序列之间的关系采用相似度方法。相似度r用来表示样本之间相似程度的度量,r越接近0,说明两个样本之间的相似度就越低;r越接近1,说明两个样本之间的相似度就越高。定义两基因序列A与B之间的相似度为:

其中,c和α为常数,这里为使rij∈[ ]0,1,本文选取c=1,α=1对距离矩阵进行相似度计算。当欧氏距离越大时,rij就越小,得到相应的模糊邻近矩阵 R=见表2。
4.2 模糊动态聚类图
基于表2的模糊相似矩阵,用Matlab编程计算得到模糊等价矩阵,从而得到动态模糊聚类图,如图1所示。
从动态聚类图1可以看出,当选取阈值为λ=0.822 6时可分为2大类:编号1、6、2、4、16、13、11、5、8、3、7、9和14的物种分为一类,其均为陆生类动物;编号10、12和15的物种分为一类,其均为水生类动物。其中每一类物种又可以进行分类,当阈值为λ=0.901 9,可分为6类:在第一大类中哺乳类动物中人类(编号1)与大猩猩(编号6)关系最近,聚为一类;牛(编号2)、原始牛(编4)和羊(编号16)同属于牛科哺乳动物,聚为一类;家犬(编号11)和狗(编号13)聚为一类;鼠(编号5)、家鼠(编号8)和田鼠(编号14)同属于仓鼠,聚为一类,弥猴(编号3)、食蟹猴(编号7)、日本猕猴(编号9)聚为一类;欧洲比目鱼(编号10)、青鳉(编号12)和紫色球海胆(编号15)聚为一类。根据不同的需求,选取适当的阈值,可得到不同的分类结果。上述聚类结果符合实际,表明双重性质方法是合理的。
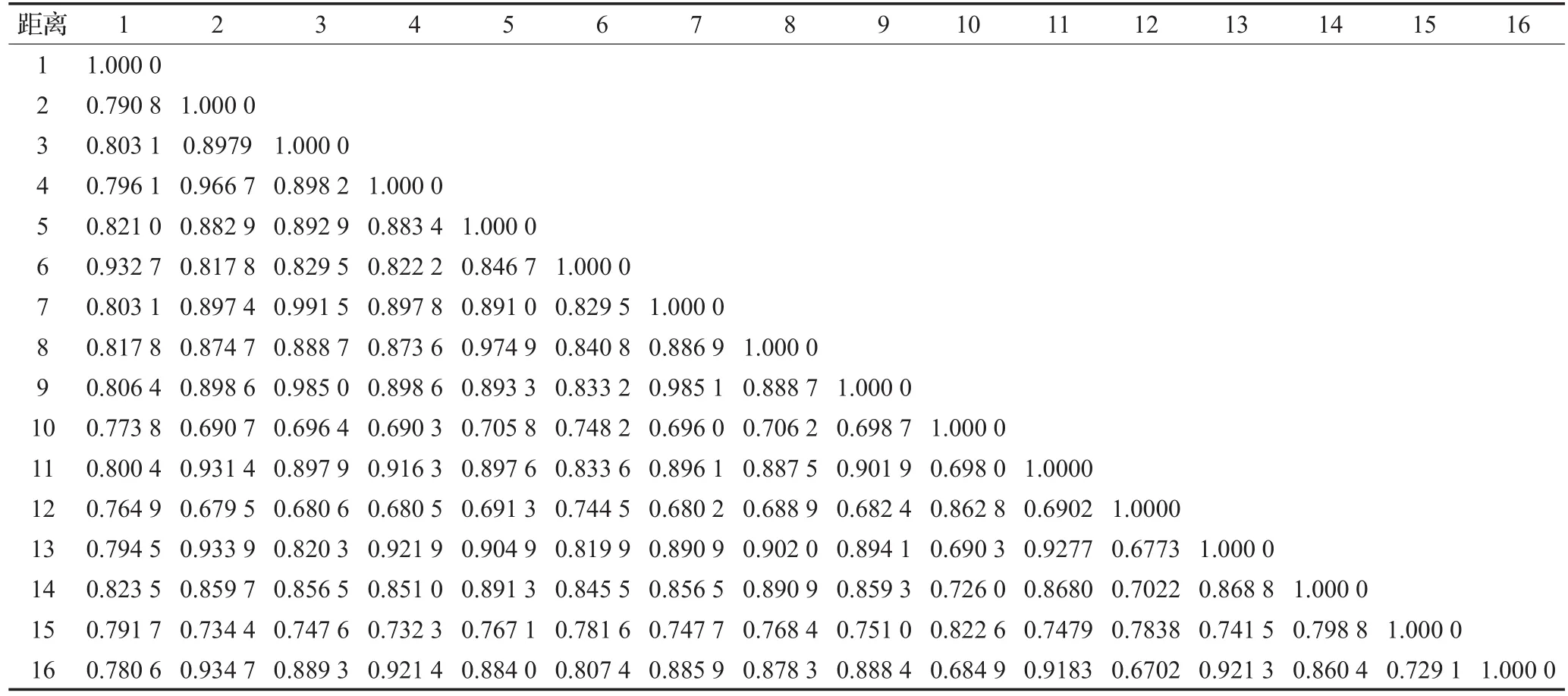
表2 由Markov转移概率和核苷酸相互作用概率模糊相似矩阵

图1 λ取不同的值时分割树形图
通过以上分析,发现利用核酸碱基对的相互作用,相当于对碱基片段AA,AT,AG,AC,TA,TT,TG,TC,GA,GT,GG,GC,CA,CT,CG和CC加权,然后再构造具有双重性质作用的距离矩阵,得到了符合实际的结果,从而可以合理地推测出碱基片段AA、TT、GG和CC在序列对比中作用较小,相反,碱基片段AC、AT、GC和GT的作用在序列对比中比其他的碱基片段作用都大。
5 层次聚类比较分析
这里用两种统计学方法的层次聚类结果来比较单一性质方法和双重性质方法,为了方便计算,先把两种性质矩阵相加,再计算序列之间的距离。利用Matlab软件编程计算得到16个物种单一性质和双重性质的欧氏距离矩阵[9]和余弦角距离矩阵[10],根据4个距离矩阵得到聚类结果如图2~5所示。
由图2和图3可知,它们的区别在紫色海胆(编号15),紫色海胆属于水生物种,和欧洲比目鱼(编号10)、青鳉(编号12)更亲近,在单一性质Markov链转移概率矩阵下,紫色海胆(编号15)和人类(编号1)、大猩猩(编号6)欧氏距离分别为0.191 7、0.202 3,和欧洲比目鱼(编号10)、青鳉(编号12)欧氏距离分别为0.166 7、0.209 0。由于它们欧氏距离差别不明显,所以图2中错误的将紫色海胆(编号15)和人类(编号1)、大猩猩(编号6)聚为一类。在双重性质距离矩阵下,紫色海胆(编号15)和人类(编号1)、大猩猩(编号6)欧氏距离分别为0.263 1、0.279 5,和欧洲比目鱼(编号10)、青鳉(编号12)欧氏距离分别为0.215 7、0.275 9。在双重性质情况下,紫色海胆(编号15)和欧洲比目鱼(编号10)、青鳉(编号12)欧氏距离都比人类(编号1)、大猩猩(编号6)欧氏距离要小,所以图3将它们聚为一类,这表明双重性质方法比单一性质方法的欧氏距离聚类结果效果更好。
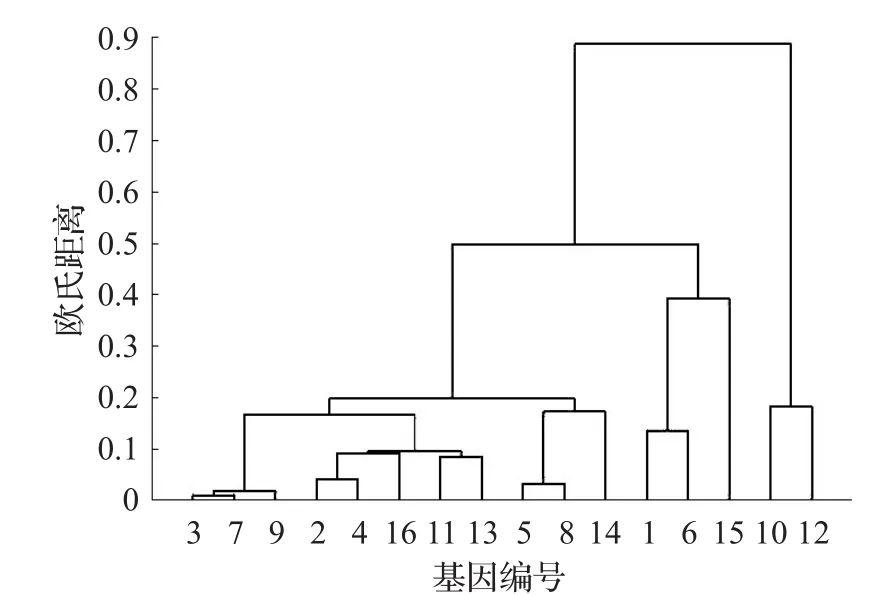
图2 单一性质欧氏距离16条基因序列聚类谱系图
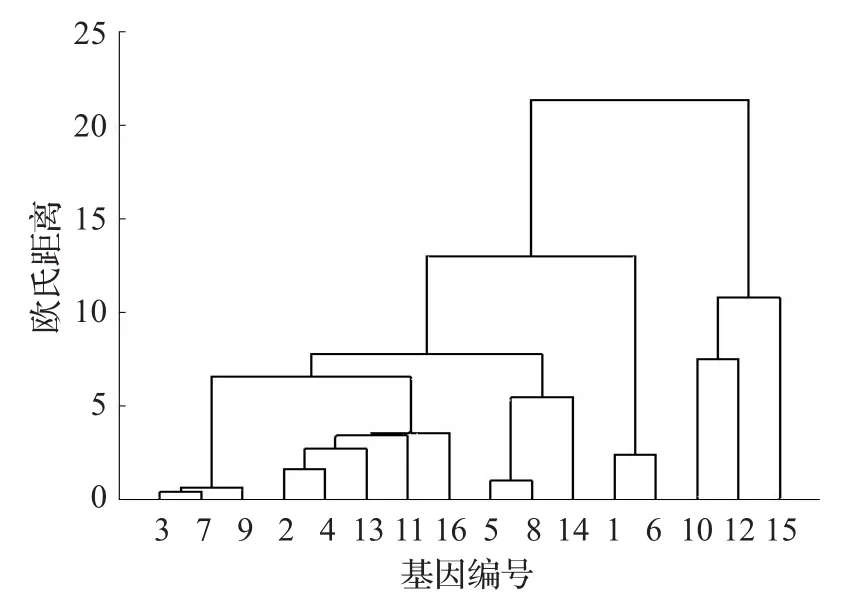
图3 双重性质欧氏距离16条基因序列聚类谱系图
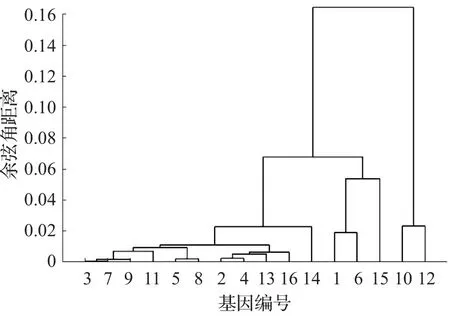
图4 单一性质余弦角距离16条基因序列聚类谱系图
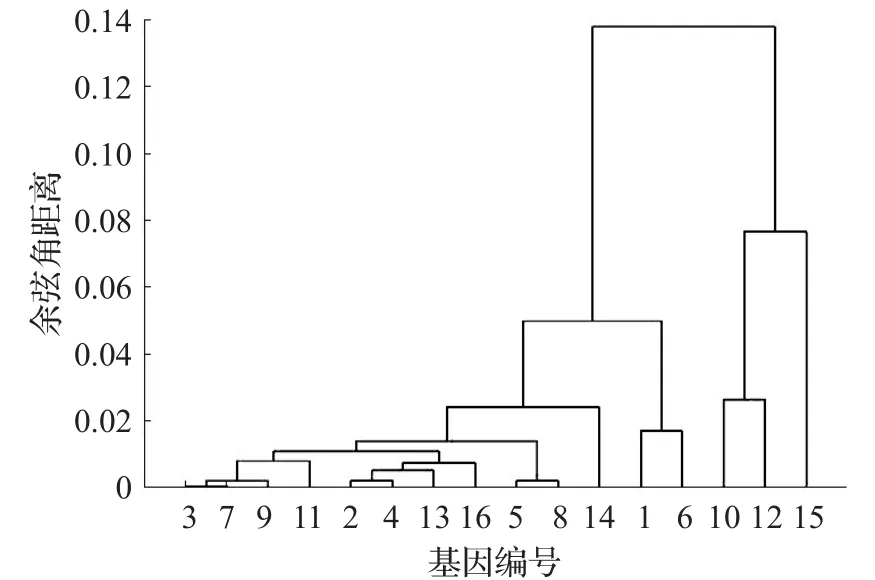
图5 双重性质余弦角距离16条基因序列聚类谱系图
由图4和图5可以看出,它们的区别在田鼠(编号14)属于鼠科动物,和鼠(编号5)、家鼠(编号8)是一类,紫色海胆(编号15)的聚类,紫色海胆(编号15)属于水生物种,和欧洲比目鱼(编号10)、青鳉(编号12)更亲近,所以具有双重性质的余弦角距离聚类结果更符合实际。
综上所述,结合两种距离方法的聚类结果对比发现,在提取基因特征中引入核酸碱基对的相互相用的方法比单一方法更准确,是一种能够较准确反映生物学中一些物种相似性信息的方法。
6 结论
本文在Markov链模型的基础上引入核酸碱基对相互作用,构成了具有双重性质矩阵的方法,采用模糊聚类方法,做出了动态聚类谱系图进行聚类分析,结果符合实际;此外,还与单一性质的特征矩阵方法作聚类结果对比,发现具有双重特征性质矩阵的方法更加准确。
在本文方法中,考虑了不同二核苷酸的潜在重要性,通过核酸碱基对的相互作用反映这些差异。从实验结果可以看出,双重性质方法比单一性质方法更加准确,这告诉人们,从多方面分析事物,才能更加准确地做出判断。
如何从二元组扩展到多元组,使核酸碱基对的相互作用得到充分利用,这将是今后的研究工作之一。
